ML lec 6-1 - Softmax Regression: 기본 개념 소개
Logistic regression

지난 시간에 공부한걸 복습
큰 값을 압축을 해서 0 ~ 1 사이의 값에 나와주면 좋겠다 해서 z의 값이 크더라도 1에 수렴하고 작아지면 0에 수렴하게 되는 시그모이드 or 로지스틱 함수가 나오게 됐다.
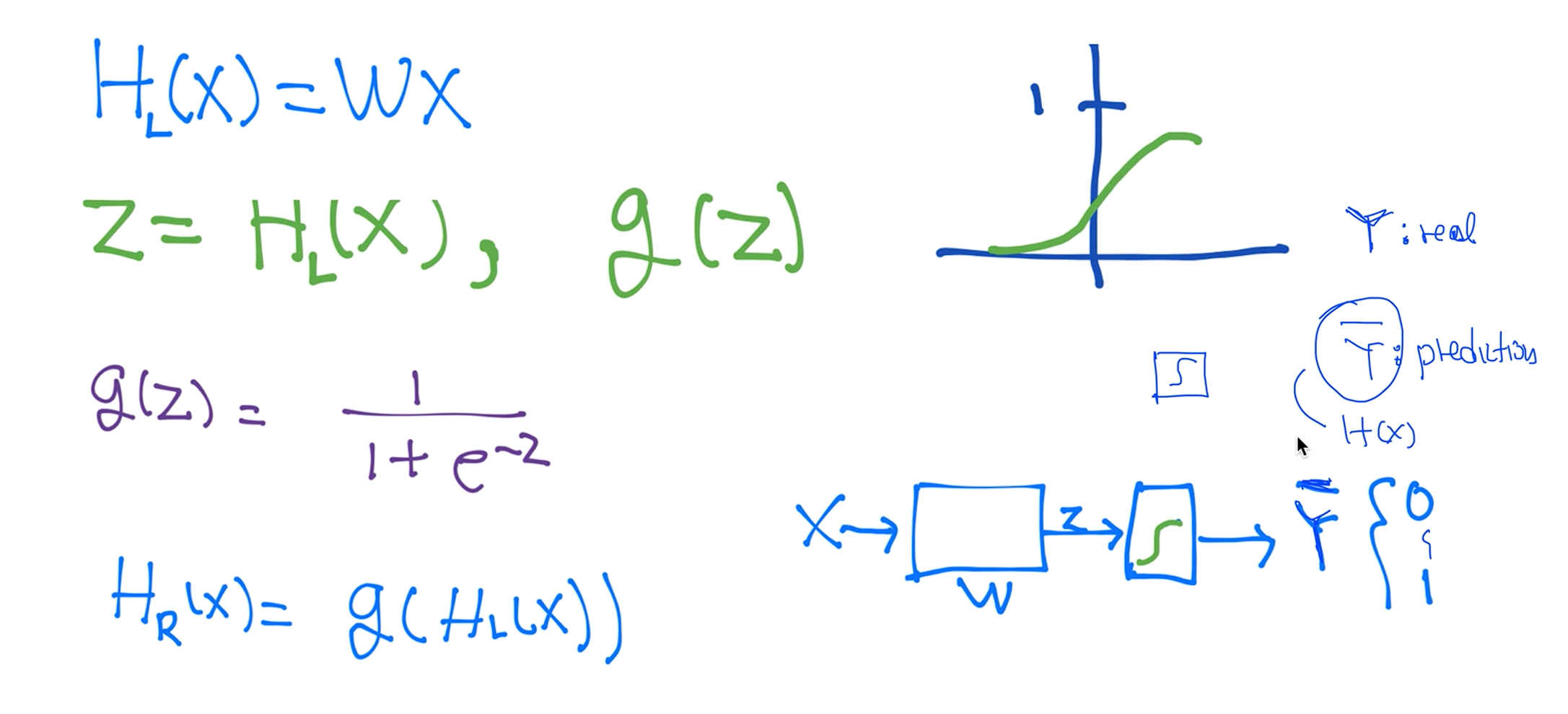
이번 시간에는 여러가지 수식들을 다뤄야 하기 떄문에 간단하게 그림으로 표현해 보았습니다.
X라는 입력이 있고, W값을 가지고 계산하는 식이 있고 그 결과값이 Z로 하고 logistic regression인 경우에는 z값을 시그모이드 함수에 넣어서 어떤 값이 나오는데 이 값은 0과 1사이가 될것이다.
통상적으로 나오는 값을 Y의 햇 이라고 많이 씁니다. Y는 실제데이터라고 하면 Y의 햇은 우리 시스템을 통해 예측한 값이라 통상적으로 H(x) = Y의 햇 이다.

직관적으로 보기 위해서 두개의 x1 x2값을 가지고 있고 분류해야 할 값들이 네모와 엑스가 있는 데이터라고 했을 때, 로지스틱 클래스피케이션을 학습시킨다는 이야기가 무엇이냐면 네모와 엑스를 구분하는 선을 찾아내는 것이다.
Multinomial classification
그러면 이 아이디어를 그대로 멀티노미얼 클래스피케이션에 적용 할 수 있다. 멀티노미얼이라는 것은 여러개의 클래스가 있다는 뜻이죠

왼쪽 데이터를 보면 몇시간을 공부했고 수업은 몇번을 왔는데 그거에 대한 학점을 줘서 우측의 그래프에 그렸습니다.

그러면 우리가 바이너리 클래스피케이션만 가지고도 멀티노미얼 클래스피케이션을 구현이 가능한데요
예를들어 하나의 클래스피케이션을 만들어서 이런 하이퍼플랜을 찾아냈습니다. 그럼 예는 무조건 C이거나 C가 아니거나 하는 걸 만들어내고, 얘는 B이거나 B가 아니거나 또 A이거나 A가 아니거나 구분하는 3개의 각각 다른 바이너리 클래스피케이션을 가지고도 구현이 가능합니다.
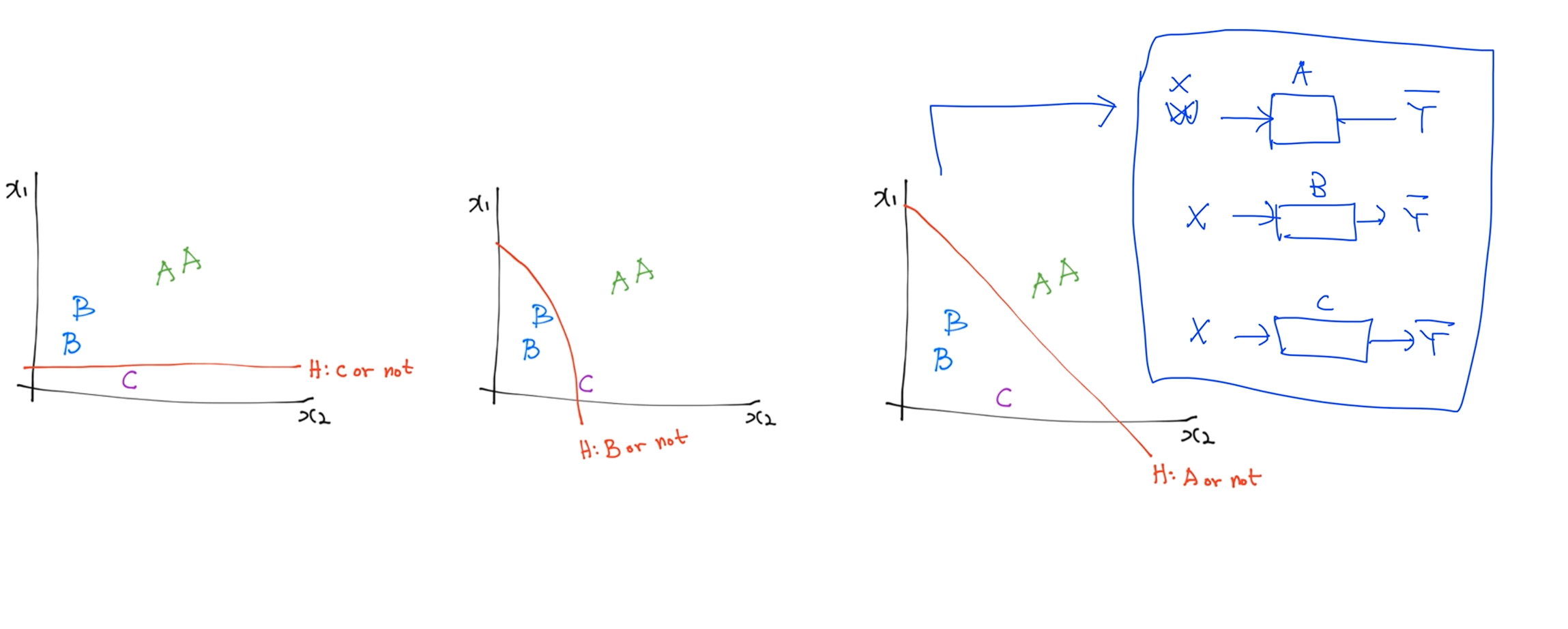
이전 슬라이드에서 소개한 그림으로 표기하면 X가 주어졌을 때 어떤 Y햇을 예측할때 3개의 독립된 도식화된 그림을 가지고 구현이 가능하다.
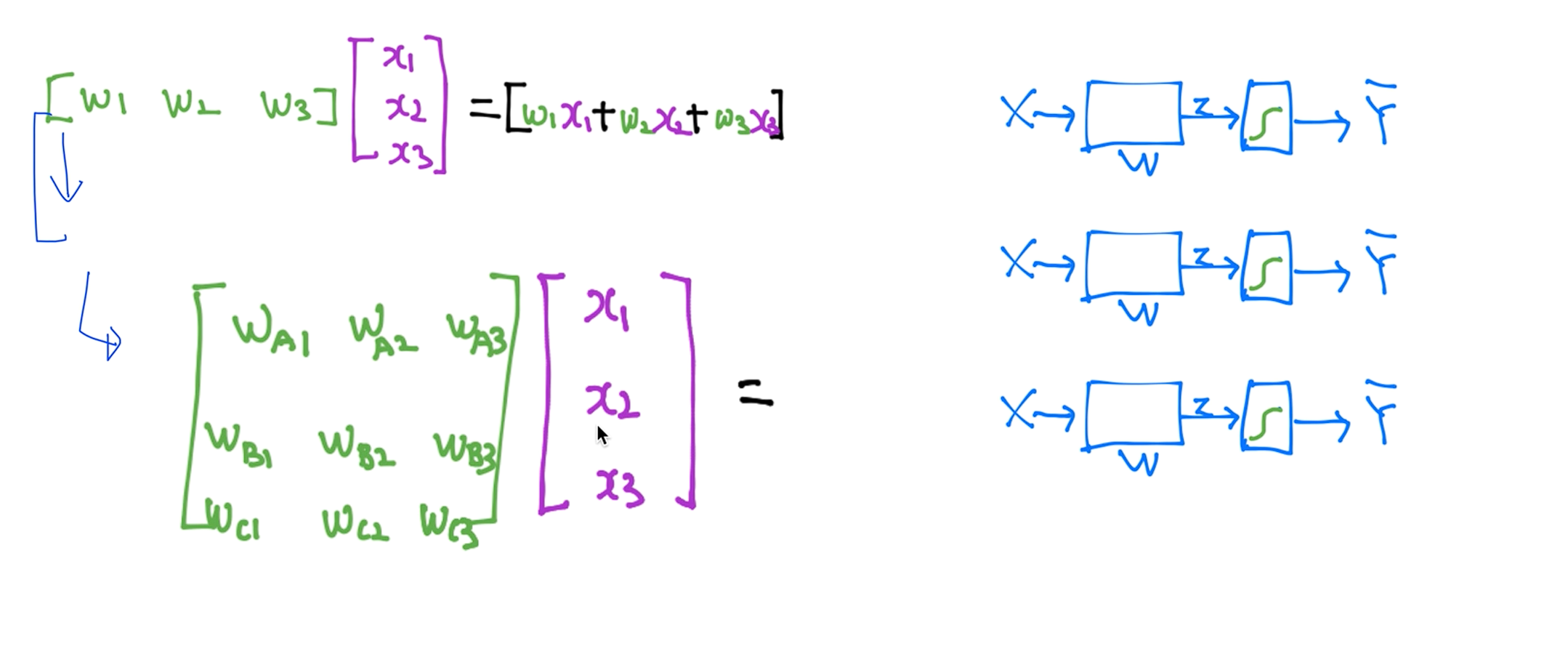
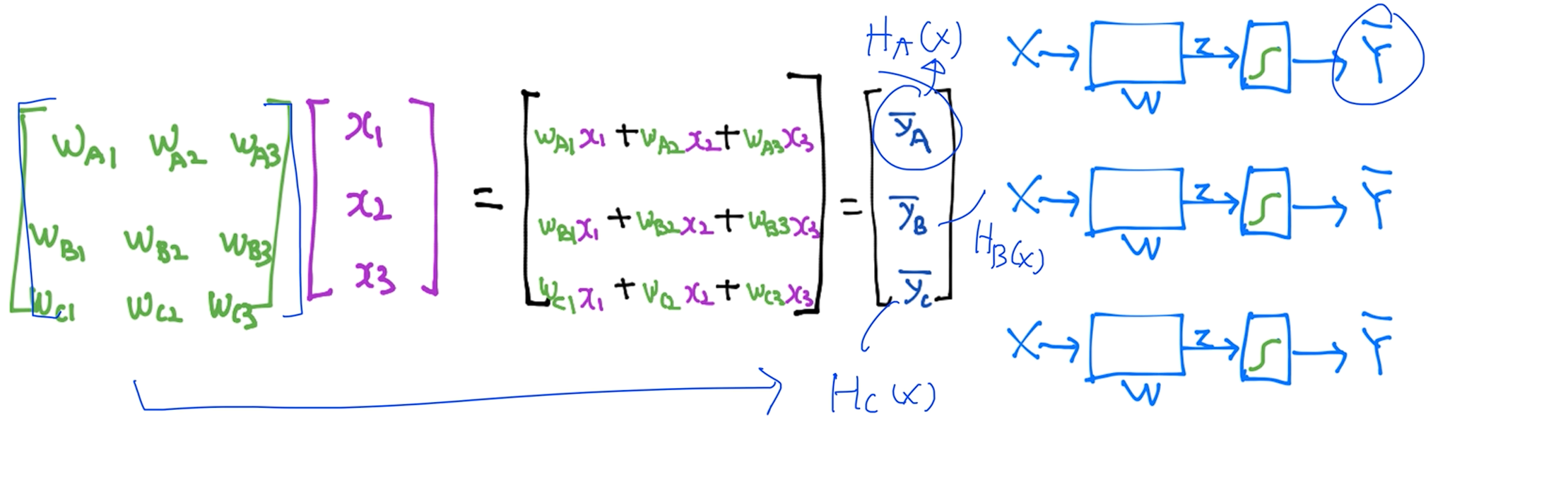
지난번에 각각 하나의 도식화된 그림을 실제로 구현할 때 이렇게 행렬로 구현합니다. 3번 독립적으로 계산하면 됩니다. 근데 이걸 하나로 합치면 행렬 곱 연산으로 나오게되는데 이게 결국 3개의 독립된 예측값이 나오게 된다.
ML lec 6-2: Softmax classifier 의 cost함수
Where is sigmoid?

우리가 각각의 클래스 파일을 갖는것보다 하나의 매트릭스로 길게 늘임으로써 마치 각각 계산하는것처럼 구현할 수 있다
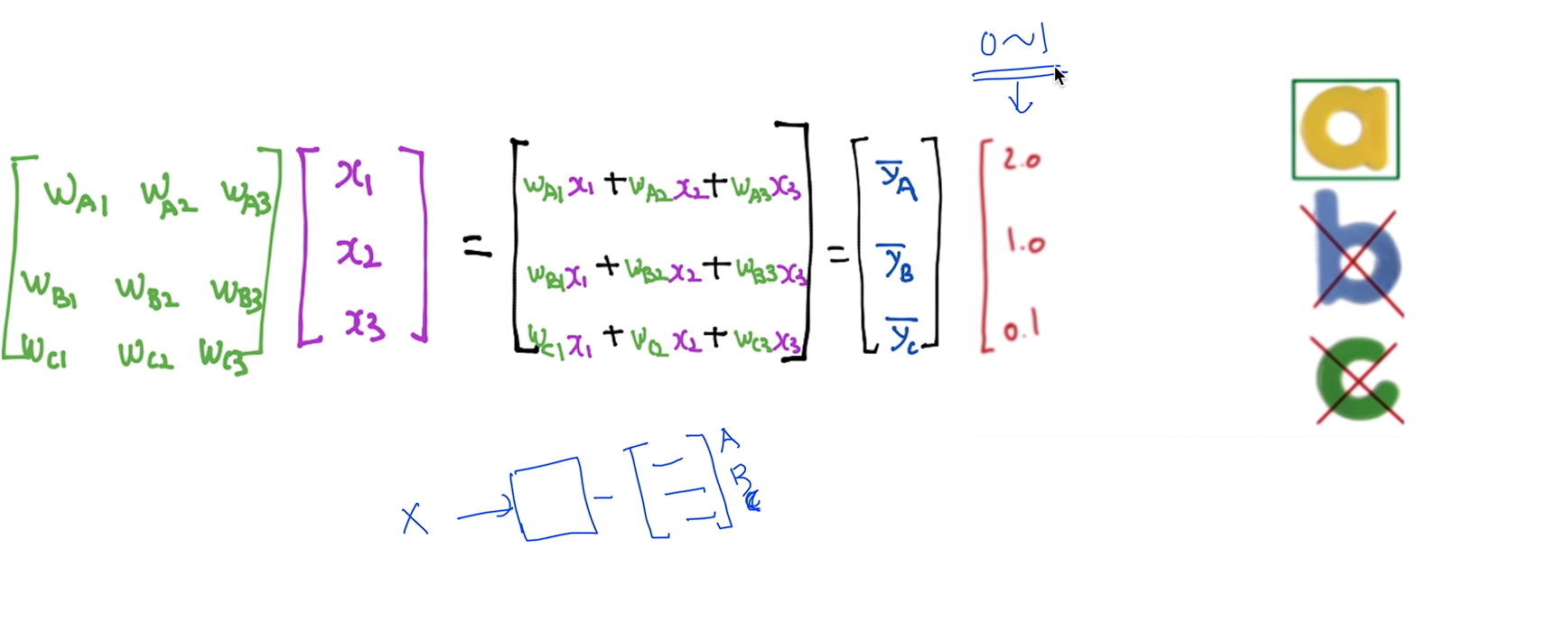
여기서 이제부터 하나의 X를 주게 되면 이전처럼 벡터로 나오게 될것입니다. 첫번째로 나오는값이 A에 해당하는 값 두번째가 B 세번째가 C 이듯이 2.0 1.0 0.1 이 나왔습니다. 그래서 답은 A인데 우리가 원하는게 아니였다.
우리가 원하는건 엄청난 큰값이 아니라 0 ~ 1 사이에서 나오는 값들이 됐으면 좋겠다하는 것이 우리의 생각이였다.
Sigmoid?

다시한번 정리를 해보면 우리가 로지스틱 클래스파이얼 써서 이런 형태로 줘서 계산을 하게 되면 이렇게 나오게 됩니다. 우리가 원하는 바는 0과 1사이의 값 그리고 이 값을 모두 더하면 1이 되는 이런형태로 표현하면 어떨까 해서 나오게 되는게 Softmax function 이다.
Softmax
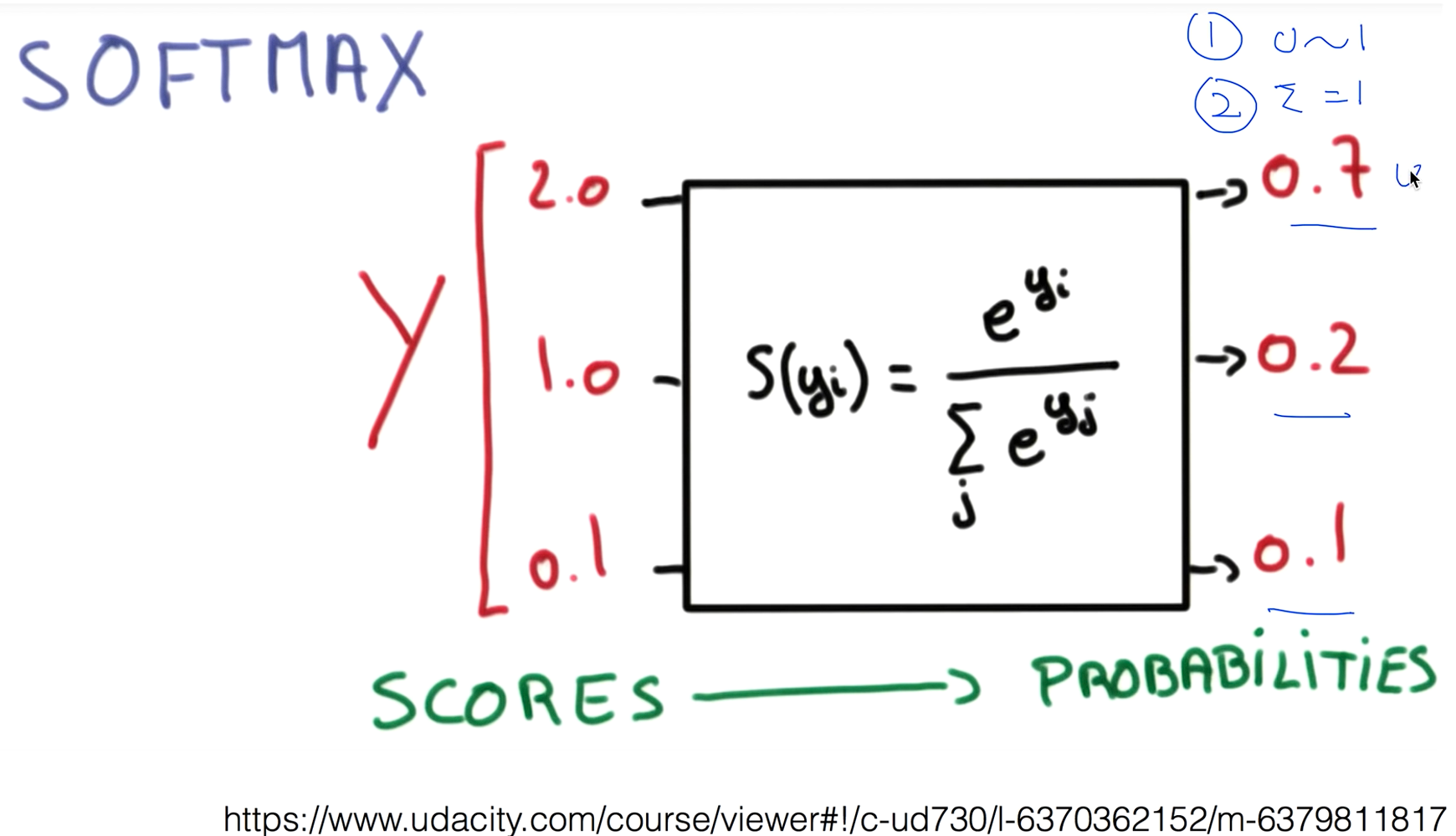
- 0 ~ 1 사이의 값이고
- 전체의 sum이 1이 되게 된다. 이 이야기는 각각을 확률로 볼 수 있다는 것이다.

이렇게 나오게 되면 이 값이 0.7 0.2 0.1을 확률로 보게 됩니다. 그 이야기는 A가 나올 확률이 0.7이고 B는 0.2 C는 0.1 확률로 나올수있겠다 라고 볼수있고 그중에 하나만 골라서 말해줘 라고 할때는 우리가 One-Hot Encoding라는 기법을 사용해서 제일 큰값을 1로하고 나머지를 0으로 만듭니다.
Cost function
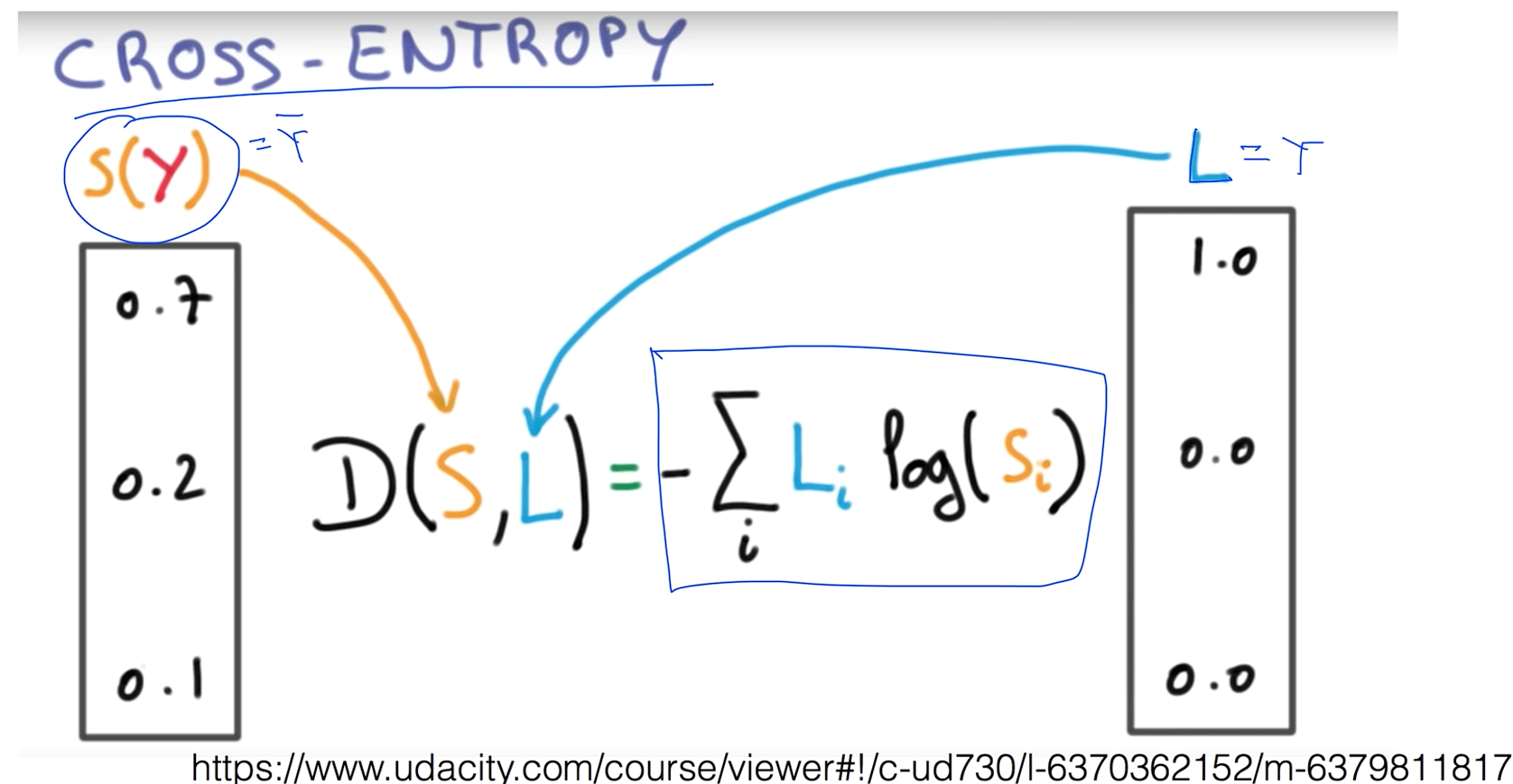
그리고 코스트 펑션도 설계를 해야하는데 여기에서는 Cross-Entropy라는 식을 쓰게 되는데 L은 Y랑 같은 실제 값이고 S(Y) 는 Y의햇 즉 예측값이라고 보면 된다. 즉 D(S, L)은 두 값 사이의 차이가 얼마나 되는지를 이렇게 생긴 크로스 엔트로피 함수를 통해서 구하게 됩니다.
Cross-entropy cost function

이 함수를 오른쪽처럼 고쳐써봤는데 -값을 안쪽으로 넣고 보면 -log쪽은 지난시간에 로지스틱 리그레이션에서 본 적이 있죠? 그래서 Y의햇 값은 SoftMax값을 통과한 값이기 때문에 항상 0에서 1사이의 값을 가집니다.
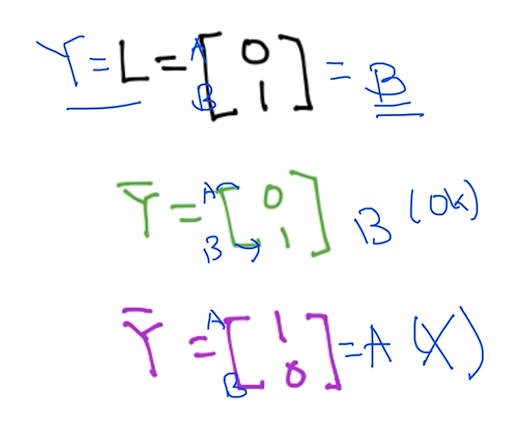
예를 들어 간단하게 하기 위해서 두가지 레이블이 있다고 가정할 때 첫번째가 A 두번째가 B일때 첫번째 Y햇은 맞은 예측이고 두번째 Y햇은 틀린 예측이다. 그래서 맞은 예측은 값이 작은값이 되고 예측이 틀리면 엄청 큰값을 주기때문에 작게 하라고 벌을 준다

그래서 예시 값들을 정의한 수식에 대입해보면 인증이 된다.
Logistic cost VS cross entropy

많은 형태의 트레이닝 데이터가 있을 경우는 한번 생각을 해봐야겠죠
이전에 로지스틱에서 코스트함수를 다뤘을 때 사실상 이 함수가 Cross-entropy라고 보면 된다.

이것이 왜 같은지는 숙제로 내보겠다. 숙제는 댓글에 잘 나와있음.
Cost function
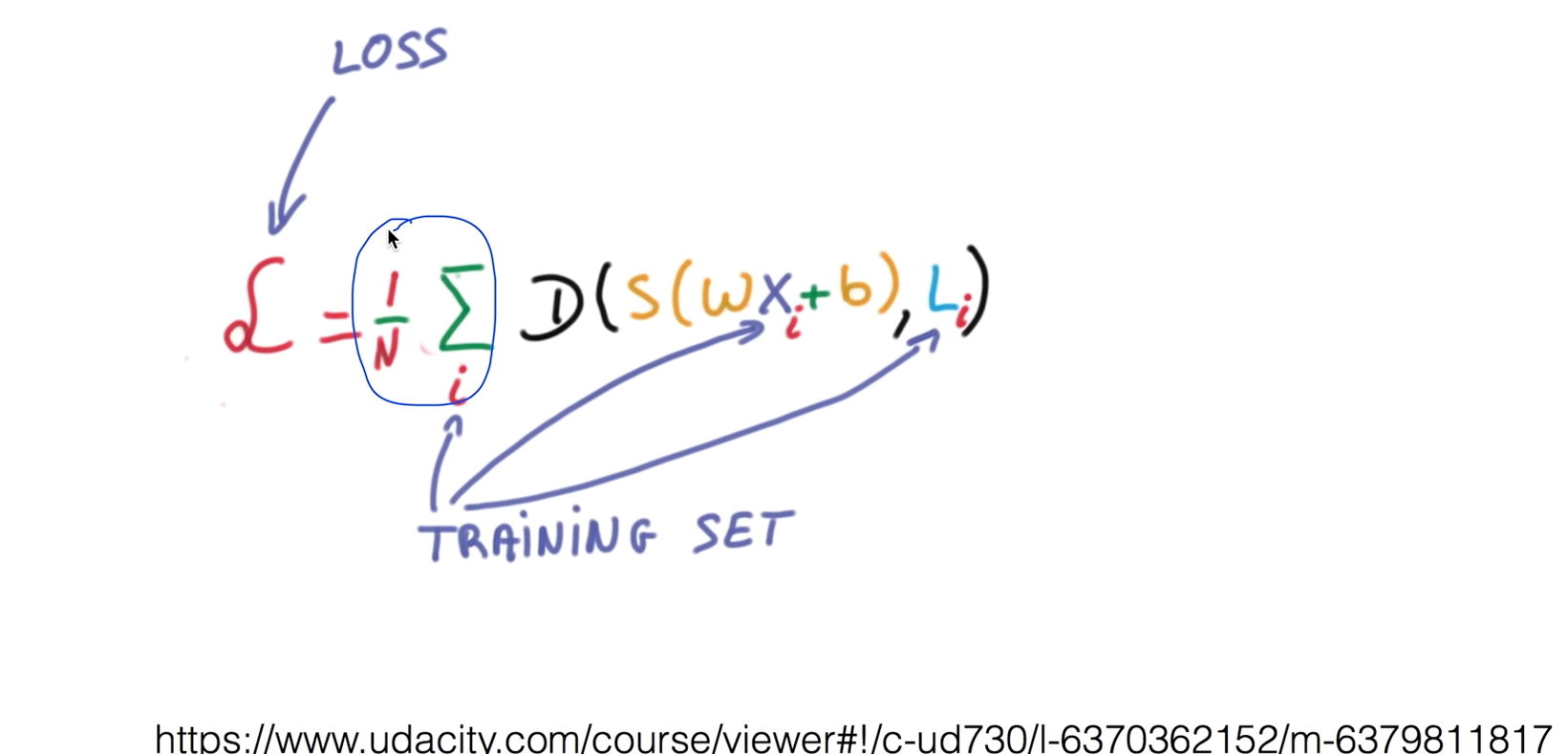
여러개의 트레이닝 셋이 있을때는 전체의 차이를 구한다음 전체로 평균을 내주면 전체의 Cost function을 정의 할 수 있습니다.
Gradient descent

마지막 단계는 코스트 펑션이 주어졌으면 코스트 펑션을 최소화 하는 값을 찾아내는 그레디언트 디센트 알고리즘을 사용하면 됩니다.
ML lab 06-1: TensorFlow로 Softmax Classification의 구현하기
Softmax function
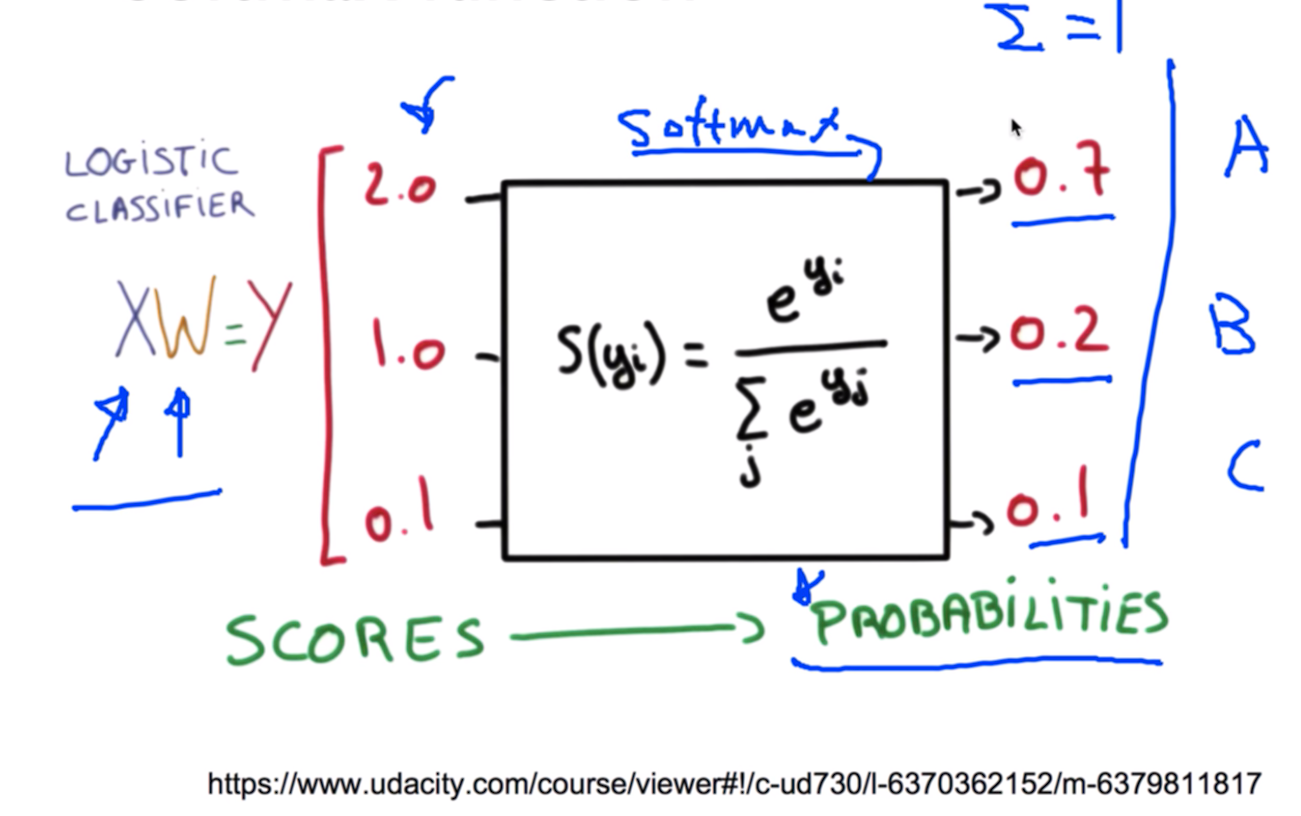
주어진 x값에 학습할 w값을 곱해서 y를 구하는걸로 시작한다.
그런데 이렇게 나오는 값들은 그냥 스코어에 불과하는데 이것을 softmax function 으로 통과시키면 이것이 확률로 나오게 된다. A가 될 확률이 0.7 B가 될 확률이 0.2 C가 될 확률이 0.1 이런식으로 확률로 정의가 가능해진다. 이것이 Softmax function
이것의 특징은 모든 클래스의 레이블의 확률을 더하게 되면 반듯이 1이 되게 된다

이 function 텐서플로우로 어떻게 구현을 하냐? 쉽다 관련 라이브러리가 있어서 쓰기도 쉽다.
Cost function: cross entropy

Test & one-hot encoding
import tensorflow.compat.v1 as tf
tf.disable_v2_behavior()
tf.set_random_seed(777) # for reproducibility
x_data = [[1, 2, 1, 1],
[2, 1, 3, 2],
[3, 1, 3, 4],
[4, 1, 5, 5],
[1, 7, 5, 5],
[1, 2, 5, 6],
[1, 6, 6, 6],
[1, 7, 7, 7]]
y_data = [[0, 0, 1],
[0, 0, 1],
[0, 0, 1],
[0, 1, 0],
[0, 1, 0],
[0, 1, 0],
[1, 0, 0],
[1, 0, 0]]
X = tf.placeholder("float", [None, 4])
Y = tf.placeholder("float", [None, 3])
nb_classes = 3
W = tf.Variable(tf.random_normal([4, nb_classes]), name='weight')
b = tf.Variable(tf.random_normal([nb_classes]), name='bias')
# tf.nn.softmax computes softmax activations
# softmax = exp(logits) / reduce_sum(exp(logits), dim)
hypothesis = tf.nn.softmax(tf.matmul(X, W) + b)
# Cross entropy cost/loss
cost = tf.reduce_mean(-tf.reduce_sum(Y * tf.log(hypothesis), axis=1))
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.1).minimize(cost)
# Launch graph
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for step in range(2001):
_, cost_val = sess.run([optimizer, cost], feed_dict={X: x_data, Y: y_data})
if step % 200 == 0:
print(step, cost_val)
print('--------------')
# Testing & One-hot encoding
a = sess.run(hypothesis, feed_dict={X: [[1, 11, 7, 9]]})
print(a, sess.run(tf.argmax(a, 1)))
print('--------------')
b = sess.run(hypothesis, feed_dict={X: [[1, 3, 4, 3]]})
print(b, sess.run(tf.argmax(b, 1)))
print('--------------')
c = sess.run(hypothesis, feed_dict={X: [[1, 1, 0, 1]]})
print(c, sess.run(tf.argmax(c, 1)))
print('--------------')
all = sess.run(hypothesis, feed_dict={X: [[1, 11, 7, 9], [1, 3, 4, 3], [1, 1, 0, 1]]})
print(all, sess.run(tf.argmax(all, 1)))
ML lab 06-2: TensorFlow로 Fancy Softmax Classification의 구현하기
softmax_cross_entropy_with_logits

Animal classification with softmax_cross_entropy_with_logits
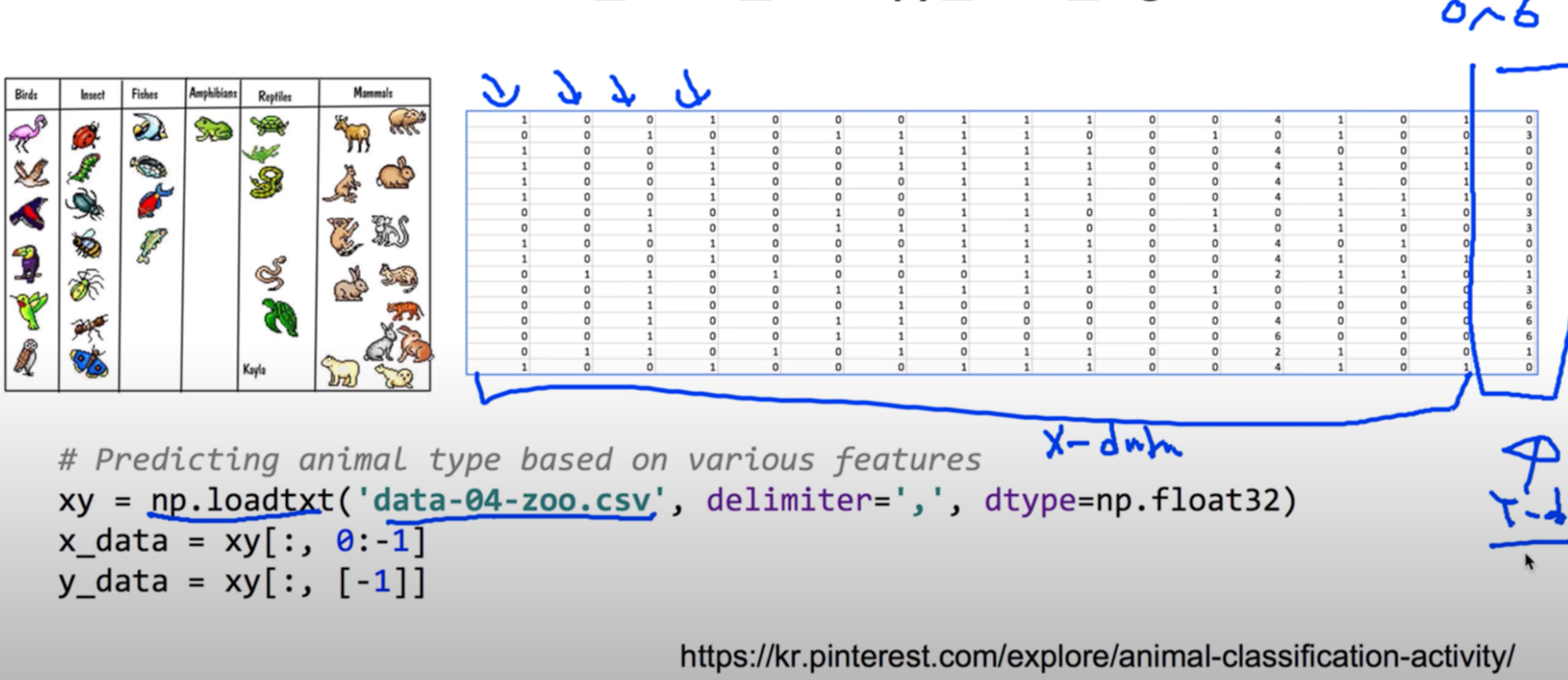
tf.one_hot andreshape

import tensorflow.compat.v1 as tf
tf.disable_v2_behavior()
import numpy as np
tf.set_random_seed(777) # for reproducibility
# Predicting animal type based on various features
xy = np.loadtxt('data-04-zoo.csv', delimiter=',', dtype=np.float32)
x_data = xy[:, 0:-1]
y_data = xy[:, [-1]]
print(x_data.shape, y_data.shape)
'''
(101, 16) (101, 1)
'''
nb_classes = 7 # 0 ~ 6
X = tf.placeholder(tf.float32, [None, 16])
Y = tf.placeholder(tf.int32, [None, 1]) # 0 ~ 6
Y_one_hot = tf.one_hot(Y, nb_classes) # one hot
print("one_hot:", Y_one_hot)
Y_one_hot = tf.reshape(Y_one_hot, [-1, nb_classes])
print("reshape one_hot:", Y_one_hot)
'''
one_hot: Tensor("one_hot:0", shape=(?, 1, 7), dtype=float32)
reshape one_hot: Tensor("Reshape:0", shape=(?, 7), dtype=float32)
'''
W = tf.Variable(tf.random_normal([16, nb_classes]), name='weight')
b = tf.Variable(tf.random_normal([nb_classes]), name='bias')
# tf.nn.softmax computes softmax activations
# softmax = exp(logits) / reduce_sum(exp(logits), dim)
logits = tf.matmul(X, W) + b
hypothesis = tf.nn.softmax(logits)
# Cross entropy cost/loss
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits_v2(logits=logits,
labels=tf.stop_gradient([Y_one_hot])))
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.1).minimize(cost)
prediction = tf.argmax(hypothesis, 1)
correct_prediction = tf.equal(prediction, tf.argmax(Y_one_hot, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
# Launch graph
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for step in range(2001):
_, cost_val, acc_val = sess.run([optimizer, cost, accuracy], feed_dict={X: x_data, Y: y_data})
if step % 100 == 0:
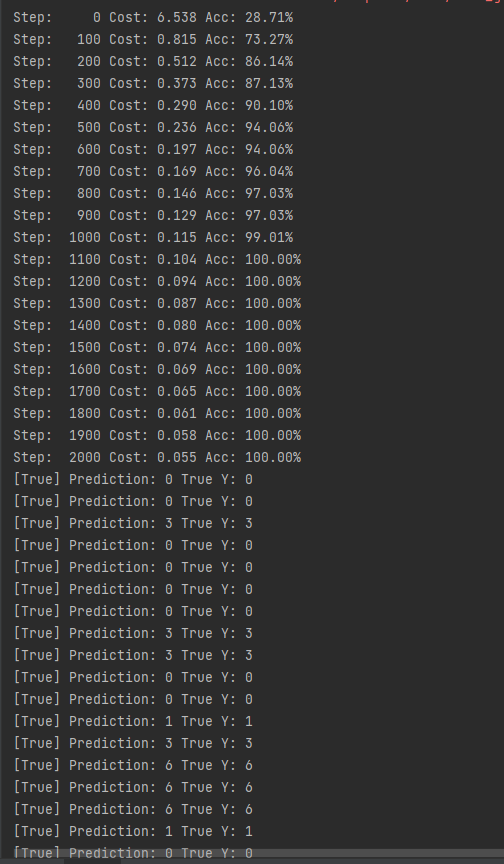
print("Step: {:5}\tCost: {:.3f}\tAcc: {:.2%}".format(step, cost_val, acc_val))
# Let's see if we can predict
pred = sess.run(prediction, feed_dict={X: x_data})
# y_data: (N,1) = flatten => (N, ) matches pred.shape
for p, y in zip(pred, y_data.flatten()):
print("[{}] Prediction: {} True Y: {}".format(p == int(y), p, int(y)))