ML 4) Support Vector machine - 1
ML 포스팅은 한학기동안 머신러닝 스터디를 하며 공부한 내용을 바탕으로 하였으며,

O’Reilly Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow, 2nd Edition을 기반으로 하고 있습니다.
1편) What is Machine Learning?
2편) Linear Regression, Gradient Descent
3편) Regularization, Logistic Regression
4편) SVM-1
5편) Decision Tree
6편) Ensemble
7편) Dimension Reduction
SVM은 다룰 내용이 많아 2번에 걸쳐 포스팅하도록 하겠습니다~!
<알아야할 용어들>
- Decision Boundary
- Margin
- Support Vector
- Kernel
- Polynomial(다항식)
- (RBF : Radial Bias Function) – 방사기저 함수
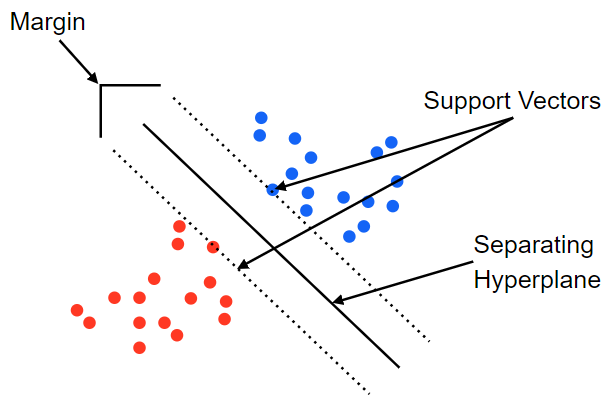
- 서포트 벡터머신이랑 결정 경계, 즉 분류를 위한 기준선을 정의하는 모델
- 분류되지 않은 새로운 점이 나타나면 경계의 어느 쪽에 속하는지 확인해서 분류 수행
- 분류를 실행시에는 Support Vector만 사용하여 계산하기 때문에 적은 계산량
 2차원 벡터들간의 결정 경계(데이터의 2개 속성이 있는 경우) : 선
2차원 벡터들간의 결정 경계(데이터의 2개 속성이 있는 경우) : 선 3차원 벡터들간의 결정 경계(데이터의 feature가 3개인 경우) : Decision boundary는 평면
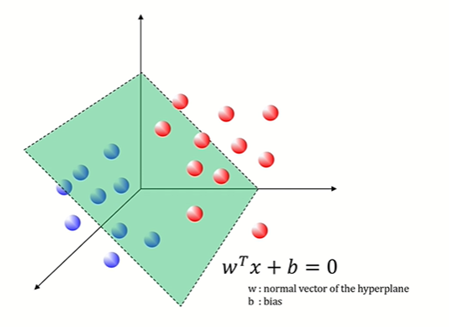
3차원 벡터들간의 결정 경계(데이터의 feature가 3개인 경우) : Decision boundary는 평면
- 속성의 개수가 늘어날수록 시각적으로는 이해할 수 없지만, 고차원의 결정경계가 생성
-> 초평면('Hyperplane') 개념
-> 초평면('Hyperplane') 일반식
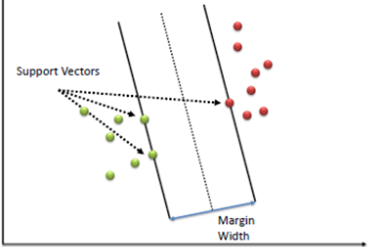
마진(Margin) - Decision boundary와의 간격
마진이 넓을수록 새로운 data에 대해 올바르게 분류할 확률이 높아짐
- 결정 경계(=Decision Boundary)를 어떻게 정의하고 계산해내는가??
- Maximizing margin over the dataset 하는 HyperPlane을 찾아야 함!
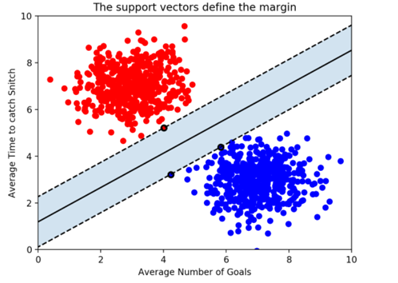
정리) SVM 모델을 만든다는 것은
“어떤 샘플들을 Support Vector로 선택해야 margin이 최대가 되는지"를 구하고, 그 샘플들의 거리를 2등분하는 직선을 구해내는 문제
최적의 Decision Boundary(=Hyperplane)는?
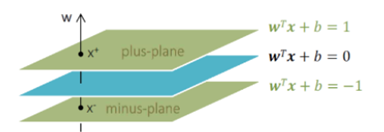 Plus plane, Minus plane 사이의 거리인 마진(margin)을 최대화하는 분류 경계면
Plus plane, Minus plane 사이의 거리인 마진(margin)을 최대화하는 분류 경계면
우리가 찾아야 하는 분류 경계면을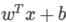 라고 할 때,
라고 할 때,
벡터 W는 이 경계면과 수직인 법선벡터
따라서 다음과 같이 표현 가능
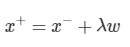 X+와 X-의 관계 : X-를 w방향으로 평행이동시키되, 이동 폭은 λ 로 스케일
X+와 X-의 관계 : X-를 w방향으로 평행이동시키되, 이동 폭은 λ 로 스케일
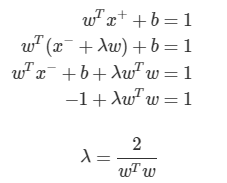

W의 L2 norm이 제곱근을 포함하고 있기 때문에 계산상의 편의를 위해 다음과 같은 형태로 목적함수를 변경
마진을 최대화하는 경계면을 찾는 문제 -> 1) 제곱 2) 역수 3) 최소화하는 문제로
Objective function(목적식)
Plus-plane보다 위에 있는 관측치들은 y=1이고, Wt x + b > 1
Minus-plane보다 아래에 있는 관측치들은 y = -1이고, Wtx + b < -1
제약식
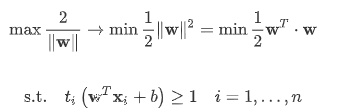
조건부 최적화 문제 (constrained optimization problem)
아래의 조건식에서, 등호가 성립하는 데이터 포인트가 서포트 벡터
n개의 선형 부등식을 가진 2차함수의 최적화 문제는 라그랑제 승수법(lagrange multiplier)이용
라그랑제 승수법?
제약이 있는 최적화 문제에서 목적함수로 제약을 옮김으로써 제약이 없는 문제로 변환하는 것
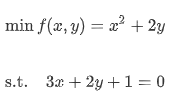 다음의 등식 제약의 조건하에서 f(x,y)를 최소화하는 x,y를 찾는 문제
다음의 등식 제약의 조건하에서 f(x,y)를 최소화하는 x,y를 찾는 문제
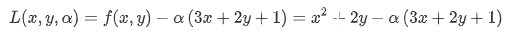
제약이 있는 최적화 문제의 해라면, 모든 partial derivative가 0인 지점이 되는 알파hat이 존재함
L(x,y,a)의 도함수가 모두 0이되는 지점 -> 최적화 문제의 해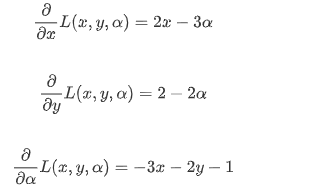
모든 함수값이 0이므로, 각각의 값 도출 가능
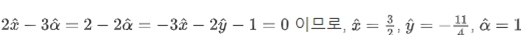
위에서 SVM 문제로 돌아가, 목적식과 제약식을 라그랑지안 문제식으로
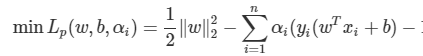
앞서 살펴본 예제는 등식 제약 조건부 최적화 문제
SVM은 부등식 제약 최적화 문제(3x + 2y + 1>= 0)
- KTT 조건 (Karush-Kuhn-Tucker 조건)을 이용한 풀이
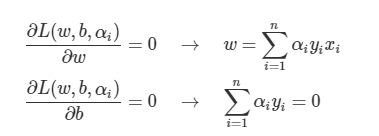 위의 식을 L에 넣어서 정리
위의 식을 L에 넣어서 정리
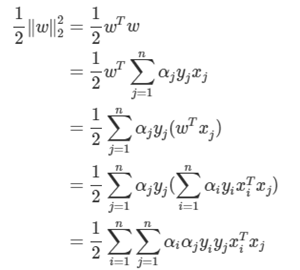
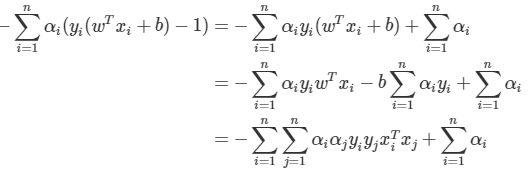
지금까지 도출한 결과를 토대로 Lp 정리
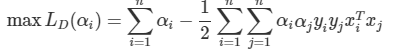
SVM의 해
최종으로 찾고자 한 마진을 최대화하는 분류경계면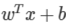 -> w와 b를 찾으면 SVM의 해를 구할 수 있음.
-> w와 b를 찾으면 SVM의 해를 구할 수 있음.
KTT조건을 탐색하는 과정에서 도출된 w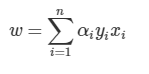
KTT조건을 만족시키는 함수가 최적값을 갖는다면 1), 2) 둘중 하나는 반드시 0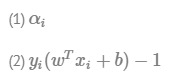
1)의 경우 알파i가 0인 관측치들은 decision boundary 형성에 영향을 미치지 못함. 즉, 마진 결정에 필요없음!
따라서 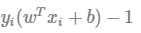 가 0인 조건을 이용해 Plus-plane, minus-plane위에 있는 벡터 즉, 서포트 벡터를 구할 수 있음
가 0인 조건을 이용해 Plus-plane, minus-plane위에 있는 벡터 즉, 서포트 벡터를 구할 수 있음
새로운 데이터에 대해 분류를 수행할 때 해당 관측치를 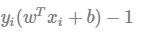 에 넣어서 0보다 크면 1, 0보다 작으면 -1 범주로 예측
에 넣어서 0보다 크면 1, 0보다 작으면 -1 범주로 예측
정리끝.... 힘들다.....
SVM Classification_Scale problem
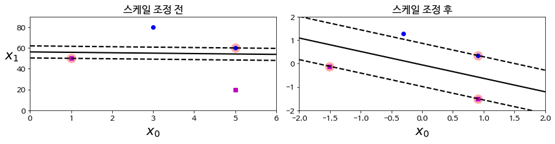 SVM은 특성의 스케일에 민감하기 때문에 모델 학습전 스케일링이 필수
SVM은 특성의 스케일에 민감하기 때문에 모델 학습전 스케일링이 필수
SVM Classification_하드마진 분류 vs 소프트마진 분류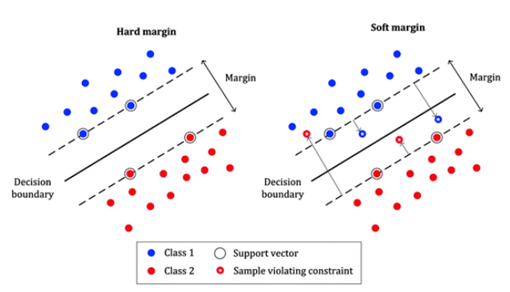 하드마진 분류 -> 선형적으로 완벽하게 분리가 가능한 경우
하드마진 분류 -> 선형적으로 완벽하게 분리가 가능한 경우
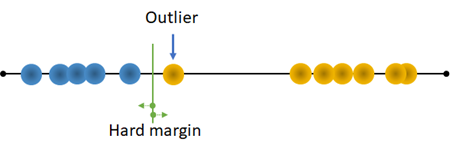 이상치에 민감한 단점
이상치에 민감한 단점
소프트마진 분류 -> 선형적으로 완벽하게 분리가 불가능한 경우
마진의 폭을 최대한 크게 유지하는 것과, 마진의 오류(샘플이 boundary 반대쪽에 있는 경우)를 고려해야 함
이를 조절하는 하이퍼 파라미터 C
: C값이 커질수록 마진오류를 최소화
SVM Classification_ Scikit-learn 장단점과 매개변수
매우 강력한 모델이며 데이터의 특성(저차원, 고차원)에 상관없이 사용가능한 모델
샘플의 수가 많은 경우에는 제한적 분류 결과에 대한 분석이 어려움
- 픽셀의 컬러 강도 같은 비슷한 단위의 특성 분류의 경우에는 매우 잘 작동함
데이터의 전처리와 매개변수의 조정 및 설정에 신경을 많이 써야하며, 높은 이해가 요구됨.
- 전처리가 필요없는 트리 기반 랜덤포레스트, 그래디언트 부스팅이 대체 가능
SVM Classification_ Scikit-learn 라이브러리로 SVM 코드 구현
class sklearn.svm.SVC(*, C=1.0, kernel='rbf', degree=3, gamma='scale', coef0=0.0, shrinking=True, probability=False,
tol=0.001, cache_size=200, class_weight=None, verbose=False, max_iter=- 1, decision_function_shape='ovr',
break_ties=False, random_state=None)
>>> import numpy as np
>>> from sklearn.pipeline import make_pipeline
>>> from sklearn.preprocessing import StandardScaler
>>> X = np.array([[-1, -1], [-2, -1], [1, 1], [2, 1]])
>>> y = np.array([1, 1, 2, 2])
>>> from sklearn.svm import SVC
>>> clf = make_pipeline(StandardScaler(), SVC(gamma='auto'))
>>> clf.fit(X, y)
Pipeline(steps=[('standardscaler', StandardScaler()),
('svc', SVC(gamma='auto'))])
print(clf.predict([[-0.8, -1]]))다음 포스팅에서는 RBF 커널을 이용한 비선형 SVM 분류모델과 SVM 회귀모델에 대해서 다뤄보도록 하겠습니다.
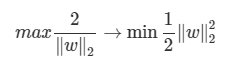
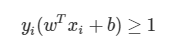

너무 유익하네요~! 잘 보고 갑니다^^