ML 5) Decision tree
ML 포스팅은 한학기동안 머신러닝 스터디를 하며 공부한 내용을 바탕으로 하였으며,
O’Reilly Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow, 2nd Edition을 기반으로 하고 있습니다.
1편) What is Machine Learning?
2편) Linear Regression, Gradient Descent
3편) Regularization, Logistic Regression
4편) SVM
5편) Decision Tree
6편) Ensemble
7편) Dimension Reduction
원래 순서대로 로지스틱 회귀와 SVM을 다뤄야 하지만, 로지스틱 회귀같은 경우에는 이론적인 이해가 부족하다고 느껴, 추후에 작성해야겠다고 마음먹은 찰나에.. 학회에서 Decision Tree 발제를 할 기회가 있어서 이참에 빠르게 ML 5편 포스팅을 이어가보도록 하겠습니다..!!
오늘 포스팅은
1) 분류 task에서의 평가지표
2) decision tree - entropy, recursive partitioning, prunning
3) decision 코드 및 grid search를 통한 하이퍼파라미터 튜닝
의 순서대로 다룰 예정입니다.
1) 분류 task에서의 평가지표
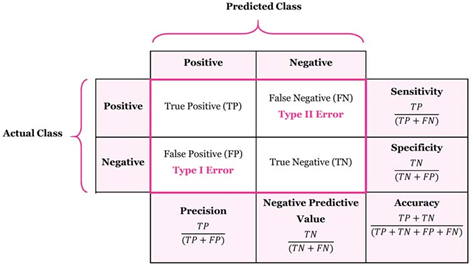
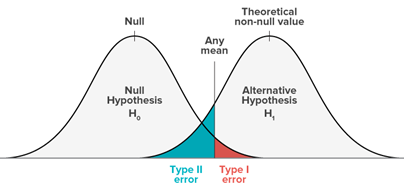
True Positive(TP) : 실제 True -> 예측 True (정답)
False Positive(FP) : 실제 False -> 예측 True (오답)
False Negative(FN) : 실제 True -> 예측 False (오답)
True Negative(TN) : 실제 False -> 예측 False (정답)
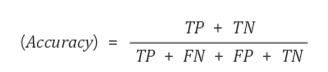
Accuracy : 총 관측치 중 올바르게 예측한 비율
Accuracy Paradox : 5번의 사기사례를 단 한번도 예측하지 못함에도, 95%의 accuracy를 보이는 문
Target 값의 실제 분포가 Imbalance한 경우 신뢰도가 떨어짐
정밀도 : 모델이 True 라고 예측한 것 중 실제 True의 비율
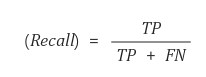
재현율 : 실제 True인 것 중에서 모델이 True라고 예측한 비율
Recall과 Precision은 Trade-off 관계
결정임계값(decision Threshold)에 따라서, 정밀도를 올리면 재현율이 내려가고, 반대로 재현율을 올리면 정밀도가 내려가는 관계
F1-score : Precision과 Recall의 조화평균. 두 지표를 균형있게 반영함
ROC curve : FPR과 TPR을 각각 x,y축으로 놓은 그래프
- TPR : True Positive Rate (=민감도, true accept rate)
1인 케이스에 대해 1로 잘 예측한 비율 - FPR : False Positive Rate (=1-특이도, false accept rate)
0인 케이스에 대해 1로 잘못 예측한 비율
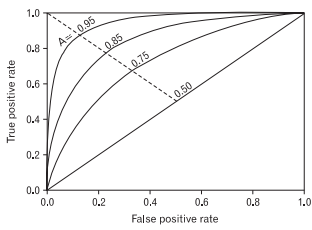
y축을 재현율(Recall) x축은 FPR(1-specificity)로 하는 그래프
ROC-AUC : ROC curve의 아랫 면적 0.5~1.0 사이의 값 1에 가까울수록 좋은 성능을 나타냄
2) decision tree - entropy, recursive partitioning, prunning
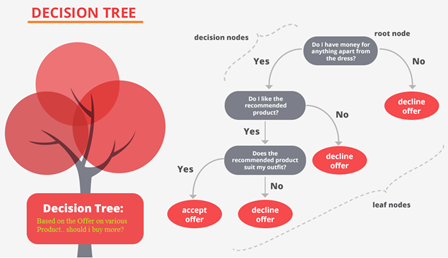
Decision Tree (의사결정나무) : 분류와 회귀가 모두 가능한 지도학습 모델
특정 질문(즉, 기준)에 따라 데이터를 구분하는 모델
한번의 분기 때마다 변수의 영역을 2개로 구분하며, 각각의 기준, 정답이 담긴 박스를 노드라고 부름
맨 처음 분류 기준(첫, 질문) : Root Node
맨 마지막 노드 : Terminal Node / Leaf Node
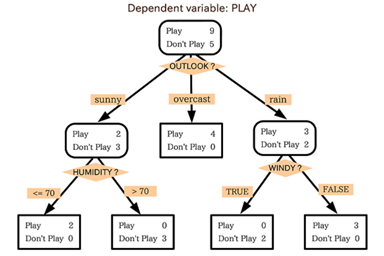
운동경기가 열릴지 열릴지 않을지 예측하기 위한 Decision Tree 모델
종속변수
Y : PLAY
독립변수
X1 : OUTLOOK(날씨) X2 : HUMIDITY (습도) X3 : WINDY(바람)
Homogeneity : 순도, 분류가 잘 된 상태를 의미
Impurity (= uncertainty) : 불순도, 불확실성, 다른 범주의 데이터가 섞여 있는 상태를 의미
순도를 나타내는 지표
1) Entropy 2) Gini index
엔트로피
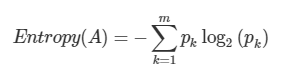
불순도(Impurity)를 수치적으로 나타낸 척도 엔트로피가 높다는 것은 불순도가 높다(=데이터가 올바르게 분류 X)는 뜻이고, 엔트로피가 낮다(=데이터가 올바르게 분류 O)는 것은 불순도가 낮다는 뜻.
엔트로피가 1 ? 한 범주 안에 서로 다른 데이터가 정확히 반반 있다 경우
엔트로피가 0 ? 한 범주 안에 하나의 데이터만 있다는 의미
<분기 전>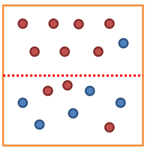
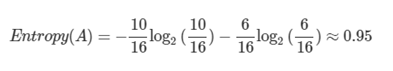<분기 후>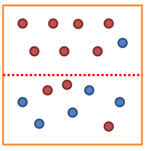
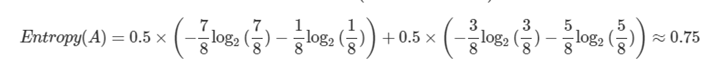
순도가 증가하고 / 불확실성이 감소 한다면?
- Imformation gain이 발생
- Information gain = entropy(parent) - [weighted average] entropy(children)
- 분기 후 엔트로피가 0.95에서 0.75으로 줄었다면? Information gain = 0.75
Process of Decision Tree
재귀적 분기(recursive partitioning)
입력변수 영역을 information gain을 최대화 하는 방향으로, 반복하며 분기하는 과정
Information gain 최대화 = Homogeneity 증가 = Impurity 감소 = Entropy 감소하는 방향으로
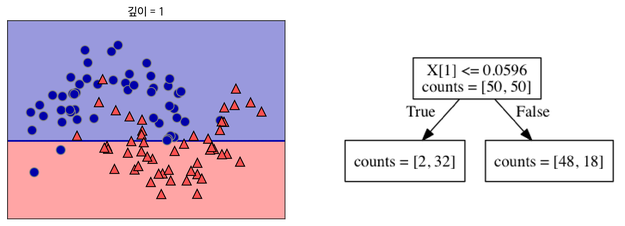
1) 데이터를 가장 잘 구분할 수 있는 질문을 기준으로 분기
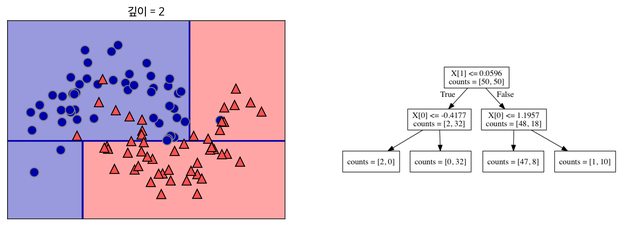
2) 나뉜 각 범주에서 다시 데이터를 가장 잘 구분할 수 있는 질문을 기준으로 분기
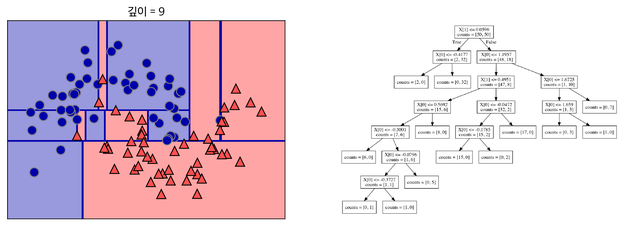
3) 분기를 지나치게 많이 한다면, train data에 과적합(overfitting)될 수 있음.
가지치기(pruning)
재귀적 분기가 끝난 후에는 모든 terminal node의 순도가 100% 인 상태 (Full tree)
과적합(overfitting)을 방지해주기 위해 적절한 수준에서 terminal node를 결합해주어야 함!
3) decision 코드 및 grid search를 통한 하이퍼파라미터 튜닝
# GridSearch는 모델 학습시에 최적의 parameter 값을 찾도록 도와주는 도구
# 꼭 Decision Tree가 아니더라도, sklearn에서 지원하는 대부분의 알고리즘에 적용 가능함
# GridSearch를 불러와주고, 새로운 tree 객체 생성
from sklearn.model_selection import GridSearchCV
grid_dt = DecisionTreeClassifier()
# 테스트 하고 싶은 parameter 값들을 parameter 별로 sequence 구조의 데이터(list, numpy array, etc...)에 넣어줍니다.
# 이 때 변수 이름은 꼭 모델 parameter 이름과 동일할 필요 X
criterion = ['gini', 'entropy']
max_depth = [3,4,5,6]
max_leaf = [16,20,24,28]
#위의 세 parameter를 하나로 묶기 위해서 다음과 같은 Dictionary 형태로
#여기서 key 값은 str 형태로, 정확하게 모델 parameter 이름과 동일해야 함
parameter_grid = {'criterion': criterion,
'max_depth': max_depth,
'max_leaf_nodes': max_leaf}
gs = GridSearchCV(estimator= grid_dt, param_grid= parameter_grid, scoring= 'f1')
# estimator는 우리가 사용하고자 하는 알고리즘 객체입니다. 위에서 할당한 grid_dt로
# scoring에는 str 형태의 인자가 들어가며. 'f1', 'roc_auc' ,'accuracy' 모두 사용 가능
gs.fit(X_train, y_train)
print('GridSearch 최적 parameter: {}'.format(gs.best_params_),
'GridSearch 최고 Validation Score: {:.3f}'.format(gs.best_score_), sep = '\n')GridSearch 최적 parameter: {'criterion': 'gini', 'max_depth': 4, 'max_leaf_nodes': 20}
GridSearch 최고 Validation Score: 0.799
의 결과를 얻을 수 있다!
