
- 본 문서에서는 반도체 8대 공정 중 두 번째 프로세스인 산화 공정에 대해서 배우게 됩니다.
- 산화 공정을 지배하는 요소는 산화물 절연체 라는 점을 염두하고 이야기를 시작합시다.
1. 개요
1.1. Oxide의 종류와 두께
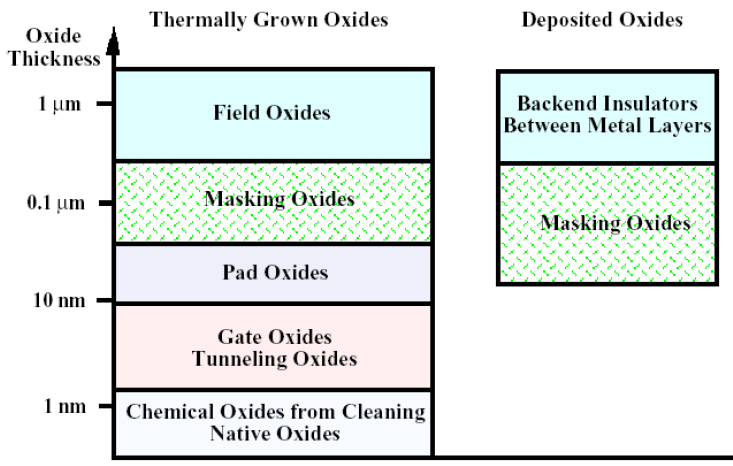
- 우리는 <2. CMOS 구조와 전체 반도체 공정> 문서에서 pad oxide, gate oxide로 를 사용한다는 사실을 배웠습니다.
- 는 와 잘 결합할 수 있고 우수한 절연특성을 가진다는 두 가지 장점 덕분에 반도체 산업에서 아주 잘 사용됩니다.
- Oxide는 열산화공정 (Thermal Oxidation)을 통해 두께가 두꺼워지는데 (=성장하는데) 용도에 따라 부르는 이름도 다르고 두께도 다르다는 점을 알고 넘어가시 바랍니다.
- Native Oxides: 열과 관련된 공정들을 거치면서 의도치 않게 성장하는 아주 얇은 층입니다. 주기적으로 제거해줄 필요가 있습니다.
- Gate Oxides & Tunneling Oxides: Gate 단자 밑에 증착되는 절연막을 의미합니다.
- Pad Oxides: 산화공정 초기에 를 보호하기 위해 웨이퍼 전체에 CVD로 증착시키는 oxide를 의미합니다. 공정이 진행되면서 gate oxide만 남기고 제거됩니다.
- Masking Oxides: 이온 주입 시 PR이 dophants를 제대로 막아주지 못 할 경우 사용합니다.
- Field Oxides: PMD, IMD#n과 같은 두꺼운 막을 의미합니다.
- 공정이 미세화되어가면서 oxide의 두께를 물리적으로 측정하는 것이 점점 어려워집니다. 따라서 절연체의 캐패시턴스 (Capacitance)를 측정한 뒤 공식으로 간접적으로 두께를 추정하는 방식을 사용합니다. 이렇게 측정한 두께를 라고 합니다.
1.2. 연속적인 산화 과정
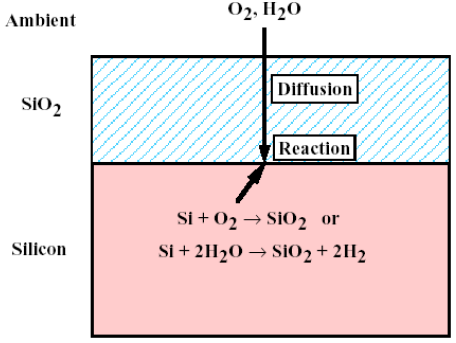
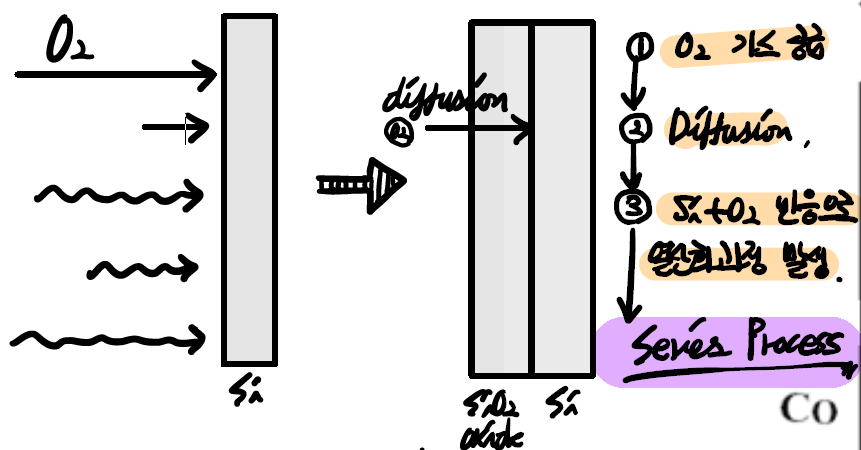
- 산화 공정에서의 oxide 확산과정은 위와 같이 세 가지 연속적인 (serial)공정으로 이뤄집니다.
- 외부 (Ambient)로부터 산화제 ()가 로 주입됩니다.
- 내부로 산화제가 아래로 확산 (Diffusion)되며 계면 (interface)에서 반응 (reaction)이 일어나게 됩니다. 확산은 에너지가 큰 쪽에서 작은 쪽으로 일어나는 현상입니다. 당연히 외부의 농도가 내부보다 높기 때문에 자연스럽게 확산이 일어납니다.
- 같은 반응에 의해 와 산화제가 반응하면서 추가적인 가 생성되면서 성장하게 됩니다.
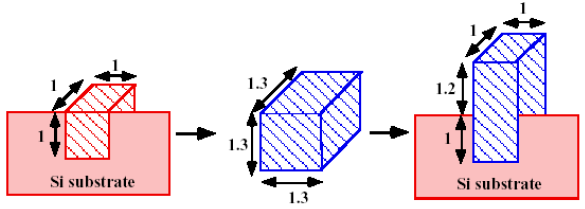
- 성장은 위와 같이 일어나게 됩니다. 단위 체적의 가 로 성장할 때는 길이가 1.3배 팽창하게 됩니다.
- 그러나 의 조밀한 원자구조 때문에 좌우로는 성장하기 어렵기 때문에 결과적으로 위로 2.2배 팽창합니다.
- 가 성장할 때 위쪽 방향, 아래쪽 방향으로 1.2 : 1 비율로 성장하게 됩니다.
1.3. C-V measurement
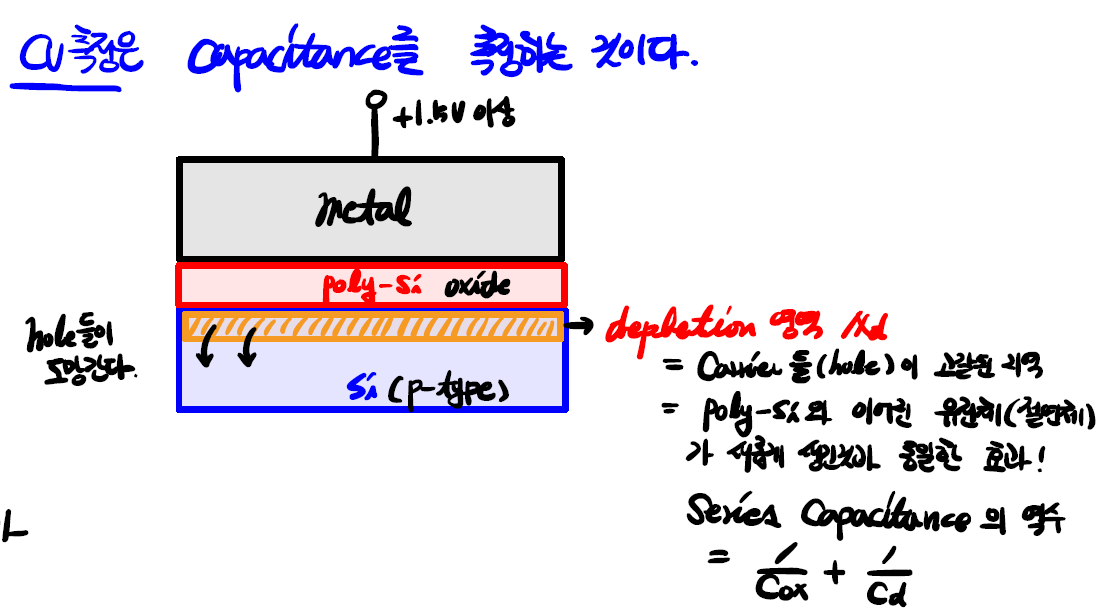
- 정상적으로 CMOS를 만들고 나면 chip 짜투리에 아주 작게
test pattern을 만듭니다. 이 부분에서 chip 내부 oxide의 capacitance를 측정하는데 이때 사용하는 방법이 C-V 측정입니다. - Gate에 양전압이 인가되면 계면의 hole들이 아래쪽으로 도망가므로 공핍층 (depletion layer)이 생긴다는 것을 이전에 설명했습니다. 또한 앞서 oxide의 얇은 두께를 간접적으로 측정하기 위해 capacitance를 사용한다고 설명했습니다.
- CV 측정은 이 공핍층이 최대 두께로 생성되는 때의 캐패시턴스를 측정해서 ① oxide의 두께를 간접적으로 추정하고 ② 문턱 전압도 측정할 수 있는 도구로 사용됩니다.
-
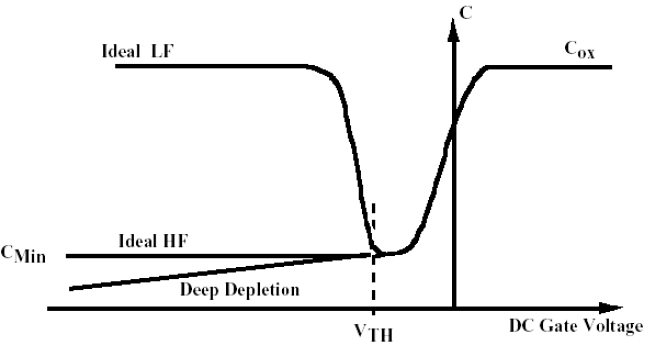
위 그림은 n-type의 wafer 기판에 대한 CV 그래프를 보여주고 있습니다.
-
이 기판은 PMOS이고 음의 전압이 인가되면 계면을 기준으로 공핍층이 생성 및 팽창되기 시작합니다. 공핍층이 팽창하면 capacitance는 문턱전압까지 계속 감소하게 됩니다.
-
그보다 더 크게 음전압을 걸어주면 인가되는 전압의 특성에 따라 두 가지 경우 중 하나의 그래프를 따라가게 됩니다.
-
LFCV (Low Frequency CV) :
인가되는 전압의 주파수가 낮아 캐리어 (전자, hole)들이 생성과 재결합을 반복하며 결국 다시 원래의 capacitance를 회복하게 되는 경우입니다.
-
HFCV (High Frequency CV) & Deep depletion :
인가되는 전압의 주파수가 매우 높아 캐피어들이 반응하지 못하고 공핍층이 계속해서 확대되는 경우입니다. 생성 및 확대되는 공핍층이 절연체 역할을 하기 때문에 capacitance가 계속해서 감소하게 됩니다.
-
1.4. Oxide에서 발견되는 4가지 전하결함
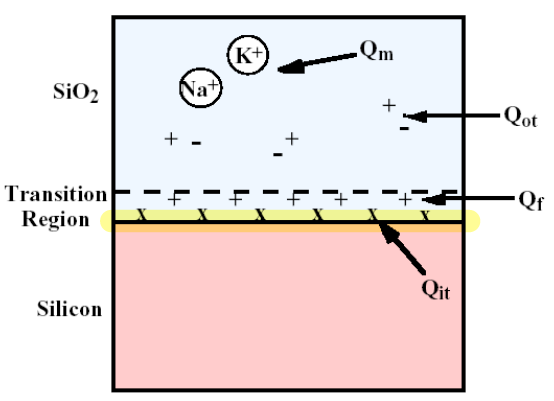
- oxide와 사이의 계면 인근에서 발견되는 4가지 전하결함이 있습니다. 간단하게 알아보고 넘어갑시다.
- : 공급되는 산화제 ()가 부족하면 반응이 정상적으로 일어나지 않고 가 생성되지 못합니다. 이렇게 비정상적으로 생성된 부산물은 전기적으로 양성을 띄는 이온 형태로 존재합니다. 이러한 이온들이 계면에 계속해서 쌓이게 된다면 전기적 potential에 영향을 미칠 것이고 결국 의도치않게 문턱전압을 낮추는 결과를 만듭니다.
- : 는 와 친화력이 좋지만 그래도 이형의 물질이기 때문에 계면에서 생기는 전자 결함을 막을 수 없습니다. 계면에서 의 원자구조가 손상되어 양이온 상태로 존재하게 되는데 이 역시 소자의 동작특성을 저해하기 떄문에 문턱전압을 바꿔버리는 결과를 낳습니다.
- : 추후에 다룰 'cleaning' 과정에서 더 자세히 다루겠지만 cleaning을 제대로 하지 못한다면 외부의 알칼리계 금속 불순물 (주로 )이 oxide 내부로 들어가서 문턱전압을 바꿔버립니다.
- : Gate oxide 자체적인 결함입니다.
2. Growth Model
이 파트에서는 의 세 가지 성장 모델에 대해서 배워볼 것입니다. 성장 모델이란 다음과 같은 의문점에서 시작해서 출발한 개념입니다.
"내가 oxide를 어느정도 두께로 성장시키기 위해서 열산화공정을 몇 시간 해줘야 하는지 알 수 있을까?"
세 가지 중 가장 기초가 되는 Deal and Grove 모델이 가장 중요하니 반드시 알아둡시다.
2.1. Deal and Grove Model
-
앞서 우리는 oxide의 성장 과정이 3가지 serial한 과정으로 일어난다는 것을 배웠습니다.
-
Serial한 과정에서 가장 중요한 점은 가장 느린 공정이 전체 속도를 지배한다는 점입니다. 즉 bottleneck에 의한 critical path가 전체 공정에 소요되는 시간을 결정하는 것이지요.
-
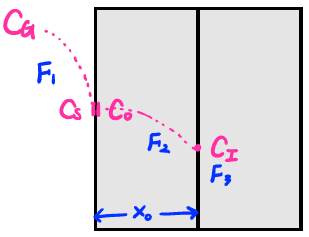
바깥의 산화제 농도를 , 바깥쪽 계면에서의 산화제 농도를 , 안쪽 계면에서의 산화제 농도를 , 계면에서의 산화제 농도를 라고 합시다.
-
단위 시간동안 단위면적을 지나간 산화제 분자의 개수를 Flux라고 합니다. 위 그림의 세 영역에서의 flux를 왼쪽부터 이라고 합시다.
- Gasphane Diffusion : 외부에서 로 들어오는 산화제 flux. 에 비례합니다. (이 공식은 헨리의 법칙을 따르며 이때 는 헨리상수라고 부릅니다.)
- Solid State Diffusion : 내부에서 확산되는 산화제의 flux. 에 비례합니다. (이때 는 확산상수라고 부르고 는 의 두께입니다.)
- Surface Reaction : 계면에서의 flux 반응식입니다. 에 비례합니다. (이때 는 비례상수 라고 부릅니다.)
-
일반적으로 은 굉장히 빠른 속도로 이뤄지기 때문에 가장 느린 공정이 될 확률이 매우 적습니다. 따라서 가장 느린 bottle neck process는 또는 둘 중 하나일 것입니다.
-
자, 고속도로를 한 번 생각해봅시다. 시간이 충분히 지나 고속도로에 병목현상이 생기게 되면 가장 느린 구간이 전체 고속도로의 진행 속도를 지배하게 됩니다. 따라서 해당 현상이 생기게 된 이후부터는 느린 구간의 속도가 전체 진행 속도가 됩니다. 이 상태를
non-transient state또는steady state라고 부릅니다. 이때부터는 입니다. -
따라서 우리는 steady state를 가정하고 방정식을 풀게 됩니다. 솔직히 우리에게 수식 유도과정은 그렇게 중요하지 않습니다. 우리는 현상과 과정을 이해하고 결과를 적절하게 잘 사용하면 되는 공학도니까요.
-
결과적으로 우리는 라는 식을 얻을 수 있습니다. 식이 너무 복잡하므로좌항의 분모를 각각 B와 B/A로 치환해봅시다. 그러면 로 나타낼 수 있고 이것이 Deal and Grove 모델의 방정식입니다. 잘 따라오셨습니다.
- 상수 B를
Parabolic rate constant라고 부르며 2번 process (Solid state diffusion)과 연관이 있는 상수입니다. - 상수 B/A를
Linear rate constant라고 부르며 3번 process (Surface reaction)과 연관이 있는 상수입니다. - 변수 를
Incubation time이라고 부르며 아무것도 없는 상태에서 초기에 있는 두께의 oxide를 생성하는 데 소요되는 시간을 의미합니다.
- 상수 B를
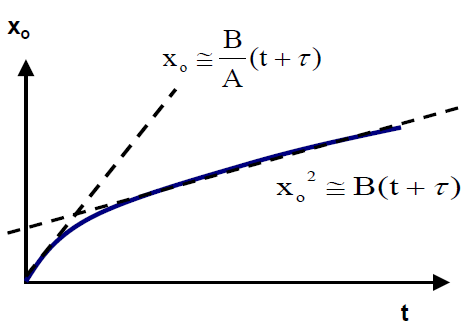
- Deal and Grove 모델은 이미 실험적으로 위와 같은 그래프 양상을 보인다는 것이 알려졌습니다.
- 가 작을 때는 B/A, 즉 3번 process가 전체 속도를 결정하게 됩니다. 따라서 위 그래프에서도 직선 (linear)그래프를 따라가는 것을 확인하실 수 있습니다.
- 가 작을 때는 B, 즉 2번 process가 전체 속도를 결정하기 때문에 곡선 (parabolic)그래프를 따라가는 것을 확인하실 수 있습니다.

-
Deal and Grove 모델은 확산 (Diffusion)을 전제로 해석한 모델이므로 기초적인 동역학을 따르게 됩니다. 동역학의 기초 식 중 아레니우스 관계식 (Arrenius Relationship)이라는 것이 있습니다. Deal and Grove 모델, 그 중에서도 우리가 방금 배운 B 상수와 B/A 상수는 아레니우스 관계식 ()를 따라 위와 같이 나타낼 수 있습니다.
- 위 식에서 는 모두
Activation Energy라고 부릅니다. 본래 에너지 차이가 존재하면 reaction은 자발적으로 자연스럽게 나타나야 합니다. 그러나 실제 산화제의 확산은 자연적으로 발생하지 않습니다. 자연적으로 확산이 발생하기 위해서는 자연상태의 원자 결합이 깨져야하고 내부에 원자가 들어갈 수 있는 공간 (Vacancy)이 존재**해야 합니다. - 이때 자연상태의 결합을 깨기 위해서 필요한 외력이 바로
activation energy입니다. - 에서 는 볼츠만 상수를 의미하고 는 절대온도를 의미합니다. 상온 (25도)에서 는 입니다. 여력이 된다면 이 값은 외워두시길 권장합니다. 자주 쓰이거든요.
- 위 식에서 는 모두
-
실험적으로 이미 상수 B와 B/A의 값은 결정되어 있습니다. 그림의 아래 표는 외부의 상태 (Ambient 또는 분위기 라고 합니다)에 따라 값이 결정되어 있습니다. 저희는 그저 이 값을 적재적소에 대입해서 쓰면 됩니다. 사용하는 방법은 간단한 예제를 들어서 이후 소개해드리겠습니다.
-
한 가지 알아두셔야 할 점은 이 값들이 (111)방향의 를 전제로 결정된 식이라는 점입니다.
-
한 가지 또 새로운 개념입니다. 알아두고 갑시다.
-
웨이퍼의 방향 - 밀러 지수 (Miller indices)
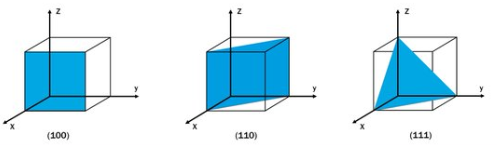
- 단결정 실리콘 재료에서 결정 방향(crystal orientation)은 Miller indices(밀러 지수)로 나타낼 수 있습니다.
- 실리콘 ingot을 위 그림처럼 좌표축에 어떻게 교차시키면서 자르냐에 따라 웨이퍼의 실리콘 단면 방향이 결정됩니다.
-
-
그러므로 만일 (100) 방향의 웨이퍼에 대한 B 상수, B/A 상수의 값을 구하고 싶다면 상단의 (111) 기준에 대한 표의 값에서 만 로 나눠주면 됩니다. (111)면이 (100)면보다 이 촘촘하게 결합이 되어있기 때문에 (100)면일 경우 가 더 낮아지게 됩니다.
Q1. 왜 (111) → (100) 면으로 바뀔 때 B/A 상수의 농도 값만 영향을 받나요?
A1. B/A 상수는 surface reaction과 연관이 있습니다. 따라서 의 단면 방향이 바뀌게 되면 surface reaction에 직접적으로 영향을 줄 수 밖에 없습니다. 반면 B 상수는 와 연관이 있기 때문에 의 단면 방향이 바뀌는 것과는 아무런 상관이 없기 때문에 값만 영향을 받습니다.
Q2. 왜 ambient에 따라 은 차이가 크고 는 차이가 별로 없나요?
A2. 은 B상수에 대한 activation energy 이므로 와 연관이 있습니다. 보다 가 더 activation energy가 낮다는 것은 더 확산이 잘 이뤄진다는 의미입니다. 왜냐하면 단순 원자량으로만 따져도 가 보다 무겁기 때문에 결합을 끊기가 상대적으로 더 어렵기 때문입니다. 그래서 같은 실리콘 결합의 빈자리 (vacency)라도 가 더 확산이 잘 됩니다
는 B/A 상수에 대한 activation energy 이고 surface reaction과 연관이 있습니다. 이 에너지는 확산보다 원자 결합을 깨는 데에 대다수 에너지를 사용합니다. 따라서 ambient 영향에 다소 둔합니다.
2.2. 2D Model
이 부분에 대한 내용은 공부가 부족해서 다루지 않습니다. 추후 채워넣겠습니다.
- Kao 박사에 의해 10년 전에 만들어진 Deal and Grove 모델에서 고려하지 않은 점들을 추가로 다룬 성장 모델입니다.
2.3. Complete process Simulation of Oxidation
이 부분에 대한 내용은 공부가 부족해서 다루지 않습니다. 추후 채워넣겠습니다.
- 2D 모델보다 더 나아가서 VLSI 제작의 거의 모든 요소를 고려하여 컴퓨팅 시뮬레이션으로 oxide 성장을 예측하는 모델입니다.
2.4. 예제를 풀어봅시다.
Q. A (111) silicon wafer is covered by an film 0.3μm thick. What is the time required to increase the thickness by 0.5μm by oxidation in at 1,200ºC?
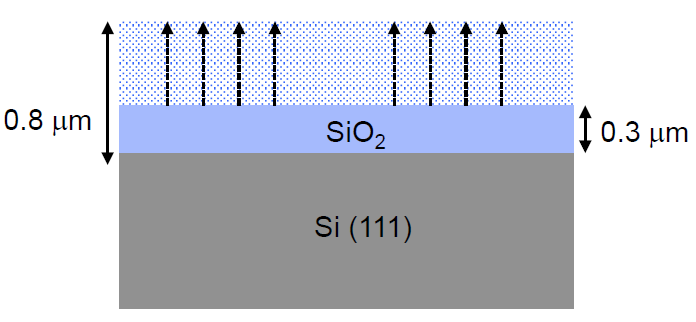
- 가 ambient 이므로 표를 참고하면 입니다.
- 위 값들을 토대로 계산해보면 입니다.
- Incubation time을 계산하기 위해 초기 두께 0.3μm이고 t = 0을 대입하면 입니다.
- 두께 0.5μm 가 추가되면 0.8μm이므로 대입하면 입니다.
- 결과적으로 두께 0.5μm를 추가로 성장시키기 위해 필요한 시간은 약 0.66 시간이라는 것을 계산할 수 있습니다.
이번 문서에서는 같은 oxide의 산화 공정과 성장 모델에 대한 내용을 배워봤습니다. 많은 내용을 담고 있어서 복잡하셨으리라 생각합니다. 그래도 예제까지 잘 따라와주셔서 감사합니다.
다음 문서에서는 포토 과정에 대해서 배울 것입니다. 다음 토픽 (포토 과정)과 다다음 토픽 (식각 과정)은 이번 문서보다는 훨씬 가벼운 정도로 훑고 지나갈 예정입니다. 읽어주셔서 감사합니다!

