Optimization Algorithm

신경망 학습의 목적은 손실 함수(Cost)의 값을 최대한 낮추는 매개변수를 찾는 것입니다
즉, 매개변수의 최적값을 찾는 행위를 최적화(Optimization)라고 합니다
하지만 매개변수의 공간은 매우 넓고 문제마다 다양하며 복잡하므로 정해진 수식을 통해 순식간에 최솟값을 구하는 방법은 불가능합니다.
더욱이 심층 신경망에서의 Hidden layer가 넓고 깊어질수록 매개변수의 수는 이에 비례하여 많아지기 때문에 최적값을 찾는 행위는 더욱 힘들게 됩니다.
이를 해결하기 위해 Cost함수에서 매개변수의 기울기(미분)을 사용하여 해당 매개변수가 기울어진 방향으로 매개변수의 가중치를 수정하는 방법을 사용합니다
이러한 방식의 시작이 되는 SGD(Stochastic Gradient Descent)및 이로부터 파생되는 최적화 알고리즘을 알아보고자 합니다.

1. SGD (Stochastic Gradient Descent)
   $W <- W - η\frac{∂L}{∂W}$
   $η (Learning Rate)$
   위 수식을 간단한 Python 코드로 나타내면 아래와 같습니다.
   
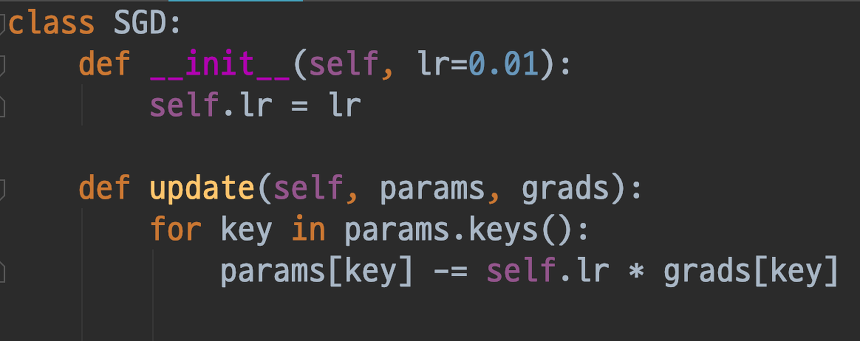
   SGD는 이렇듯 기울어진 방향으로 정해진 일정 거리만 가겠다는 단순한 방식입니다.
   이렇게 간단하고 구현도 쉽지만 문제에 따라서는 비효율적일 때가 있어 최솟값 수렴이 늦어지거나 되지 않는 경우가 있습니다.
   
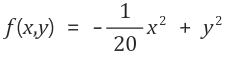
   위와 같은 함수의 등고선은 y축 방향의 기울기는 크고 x축 방향의 기울기는 완만한 볼록함수(convex function) 모양이 되는데 최솟값이 되는 지점은 (0,0) 지점이지만 각 지점에서의 기울기가 가르키는 방향은 (0,0) 방향이 아닌 y축의 가파른 기울기를 가르키게 됩니다.
   
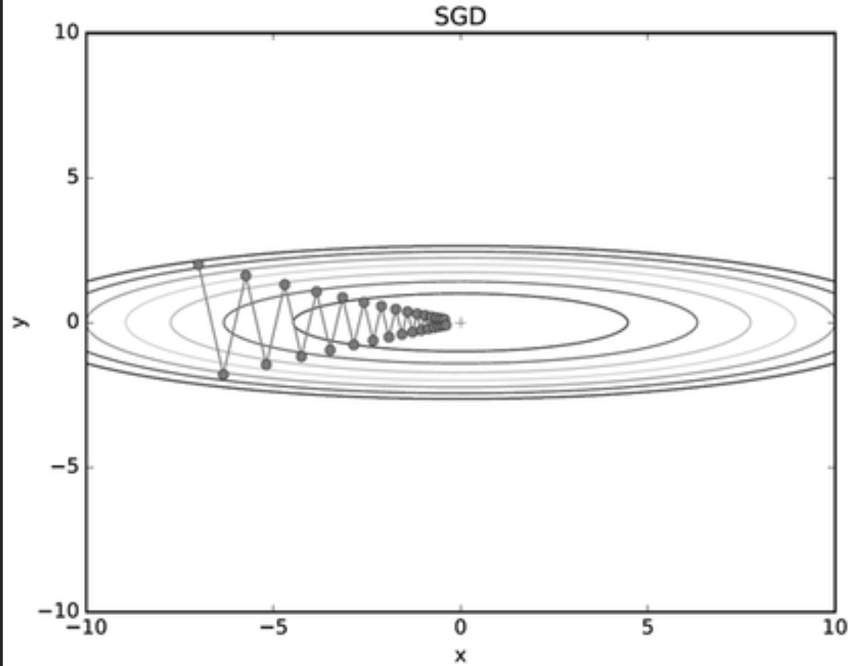
   결국 학습을 진행하면서 최적의 매개변수를 찾는 과정이 매우 비효율적으로 이루어지게 됩니다.
   즉 SGD의 단점은 비등방성 함수, 방향에 따라 기울기가 달라지는 함수에서는 탐색 경로가 비효율적이라는 점이 단점입니다.
   이러한 점에서 단순한 기울어진 방향으로 나아가는 방법보다 더 나은 방식을 고려해야 합니다.

2. Momentum
   Momentum은 '운동량'을 뜻하는 단어로, Gradient Descent를 통해 이동하는 과정에 일종의 '관성'을 주는 방식입니다.
   현재 계산된 Gradient와는 별개로 과거에 이동했던 방식을 기억하면서 그 방향으로 일정 정도를 추가적으로 이동하는 방식입니다.
   SGD가 좌우로 진동하는 현상이 발생하는 문제에서도 Momentum은 자주 이동하는 방향에 관성이 걸리게 되어 최솟값으로의 이동에 힘이 실리게 되므로 상대적으로 SGD에 비해 빠른 수렴이 가능합니다.
   수식과 간단한 Python 코드는 아래와 같습니다.
   
   
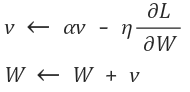
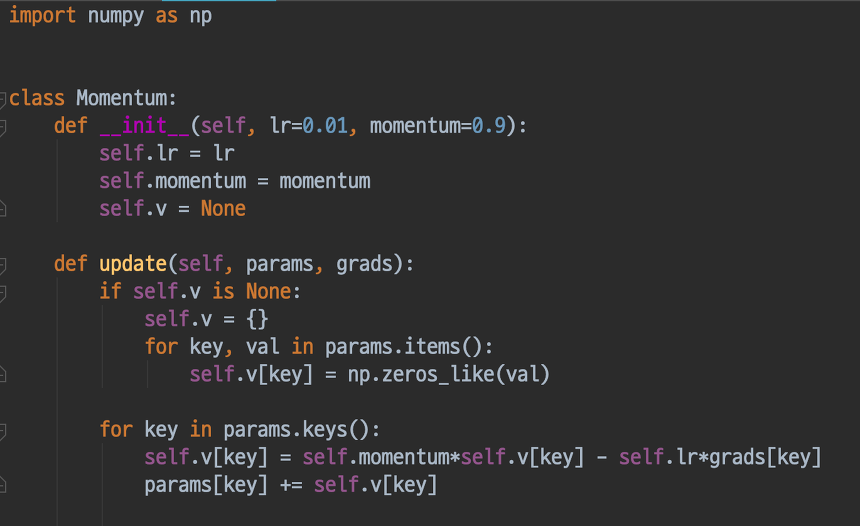
   v라는 변수는 물리에서 말하는 속도(velocity)에 해당합니다.
   αv항은 물체가 아무런 힘을 받지 않을 때 서서히 하강시키는 역할을 합니다.
   (α=0.9 등의 값으로 설정)
   
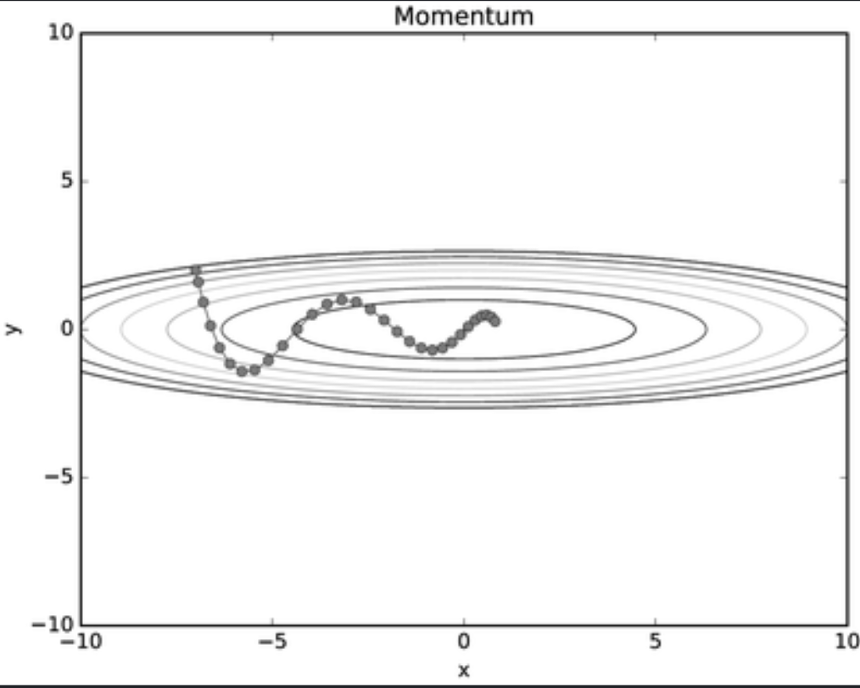
   동일한 문제에서 x의 힘은 아주 작지만 변하지 않아서 한 방향으로 일정하게 가속하지만 y축의 힘은 크지만 위아래로 번갈아 받아서 상충하여 방향 및 속도는 일정하지 않습니다.

3. AdaGrad
   신경망 학습에서는 학습률 값이 중요합니다.
   너무 작으면 최솟값으로 이동하는 정도가 지나치게 작아져 학습 시간이 너무 길어지고, 반대로 너무 크면 발산하여 학습이 제대로 이루어지지 않습니다.
   이러한 학습률을 정하는 효과적 기술로 학습률 감소(Learning Rate Decay)가 있는데 이는 학습을 진행하면서 처음에는 크게 학습하다가 조금씩 작게 학습하면서 학습률을 점차 줄여가는 방법입니다.
   가장 간단한 방식은 매개변수 전체의 학습률 값을 일괄적으로 낮추는 방식이지만 이를 더욱 발전시킨 것이 각각의 매개변수에 맞춤형 학습률을 제공하는 방식인 'AdaGrad'입니다.
   AdaGrad는 개별 매개변수에 적응적으로(Adaptive) 학습률을 조정하면서 학습을 진행하는데 지금까지 많이 변화하지 않은 변수들은 step size를 크게 하고 지금까지 많이 변화했던 변수들은 step size를 작게 하자는 컨셉입니다
   자주 등장하거나 변화를 많이 한 변수들의 경우 optimum에 가까이 있을 확률이 높기 때문에 작은 크기로 이동하면서 세밀한 값을 조정하고 적게 변화한 변수들은 optimum값에 도달하기 위해서는 많이 이동해야할 확률이 높기 때문에 먼저 빠르게 loss값을 줄이는 방향으로 이동하려는 방식입니다.
   특히 word2vec와 같이 word representation을 학습시킬 경우 단어의 등장 확률에 따라 variable의 사용 비율이 확연하게 차이나기 때문에 Adagrad와 같은 학습 방식을 이용하면 훨씬 더 좋은 성능을 거둘 수 있을 것입니다.
   수식 및 Python 코드는 아래와 같습니다.
   
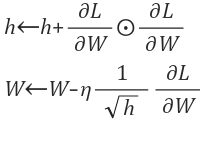
   h는 기존 기울기 값을 제곱하여 계속 더해줍니다 (기울기 행렬의 원소별 곱셈)
   그리고 매개변수를 갱신할 때 1/sqrt(h)를 곱해 학습률을 조정합니다.
   이로 인해 매개변수의 원소 중에서 크게 갱신된 원소는 학습률이 낮아지게 됩니다
   AdaGrad는 과거의 기울기를 제곱하여 계속 더해가므로 학습을 진행할수록 갱신 강도가 약해집니다.
   실제로 무한히 계속 학습한다면 어느 순간 갱신량이 0이 되어 전혀 갱신되지 않게 됩니다.
   이를 개선한 기법으로 RMSProp이라는 방법이 있는데 과거의 모든 기울기를 균일하게 더해가는 것이 아니라, 먼 과거의 기울기는 서서히 잊고 새로운 기울기 정보를 크게 반영합니다.
   즉 지수이동평균이라 하여 과거 기울기의 반영 규모를 기하급수적으로 감소시킵니다.
   
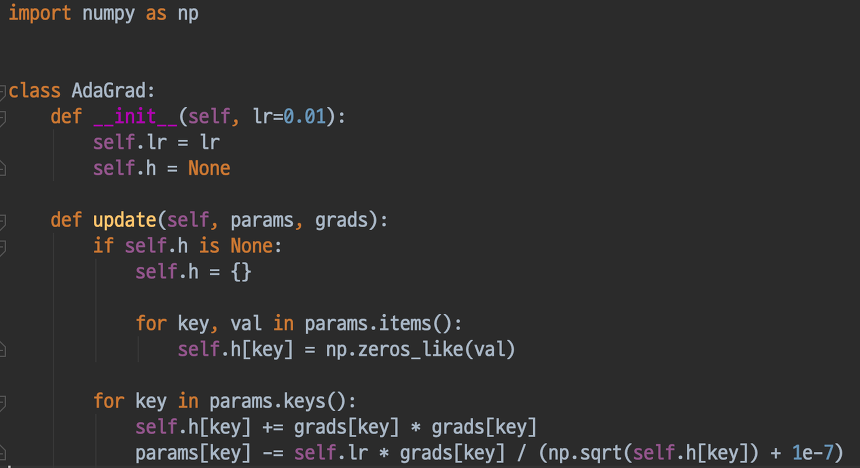
   마지막 줄의 1e-7을 더하는 부분은 self.h[key]에 0이 담겨 있다해도 0으로 나누는 사태를 막아주며 대부분의 딥러닝 프레임워크에서도 이 값을 인수로 설정이 가능합니다.
   
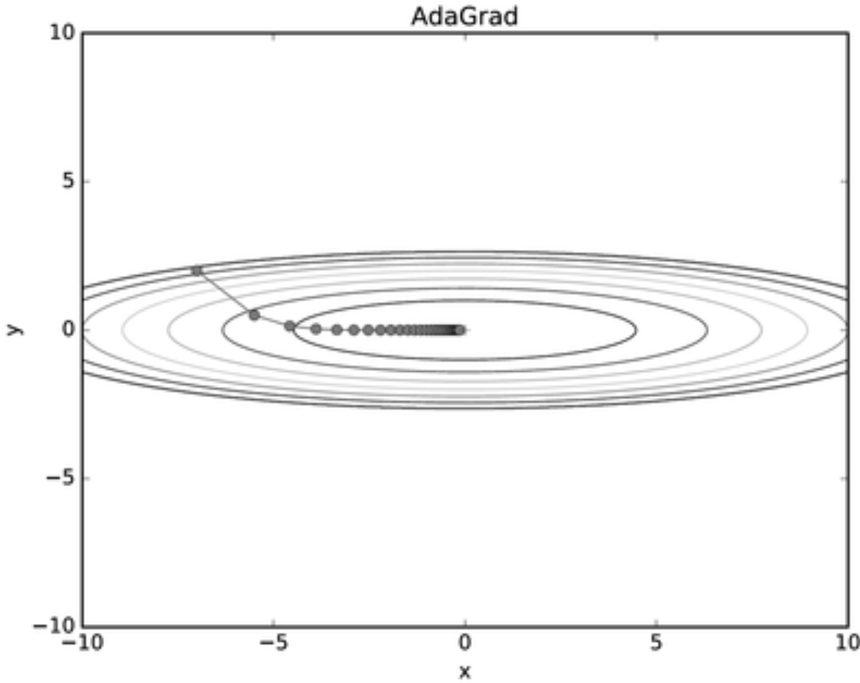
   위 등고선을 보면 y축 방향은 기울기가 커서 처음에는 크게 움직이지만 그 움직임에 비례해 갱신 정도도 큰 폭으로 작아지도록 조정됩니다.
   그래서 y축 방향으로 갱신 강도가 빠르게 약해지고 좌우반동 움직임이 크게 줄어듭니다.

4. Adam
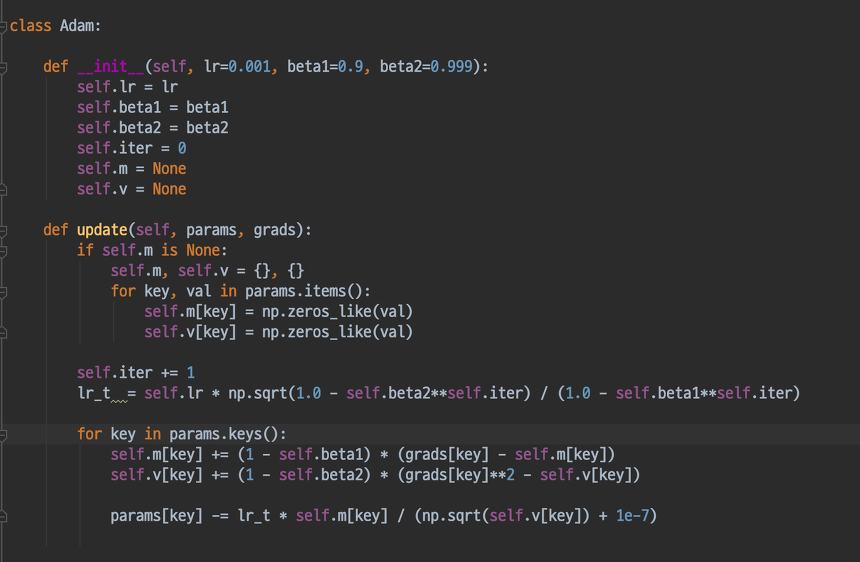
   Momentum과 매개변수마다 갱신 정도를 조정하는 AdaGrad, RMSProp 방식을 융합한 기법으로서, Momentum 방식처럼 지금까지 계산해온 기울기의 지수 평균을 저장하며 RMSProp과 유사하게 기울기의 제곱값의 지수평균을 저장합니다.
   간단한 Python 코드는 아래와 같습니다.
   
   

Summary

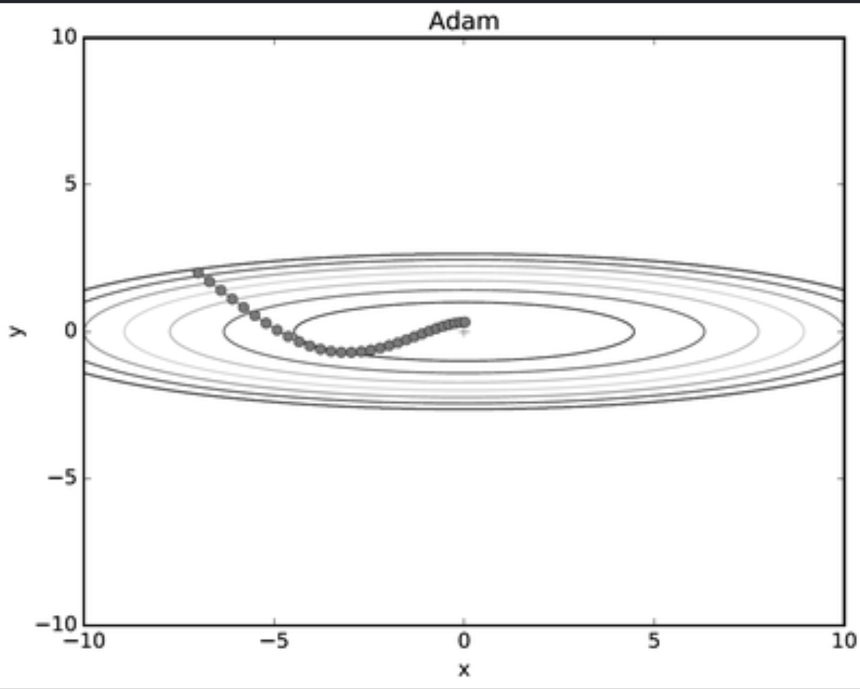
예시로 사용한 문제에 대해서는 지금까지는 AdaGrad가 가장 나았지만 실제로는 풀어야 할 문제가 무엇이느냐에 따라 달라지게되며 Optimizer별 수렴 과정을 시각화한 이미지는 아래와 같습니다.



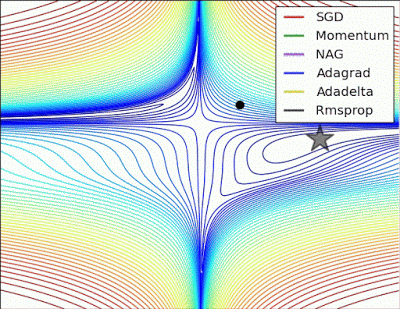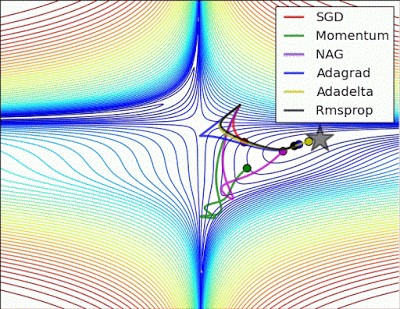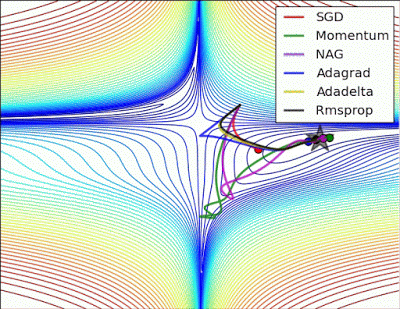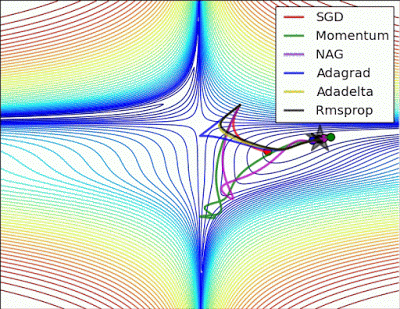
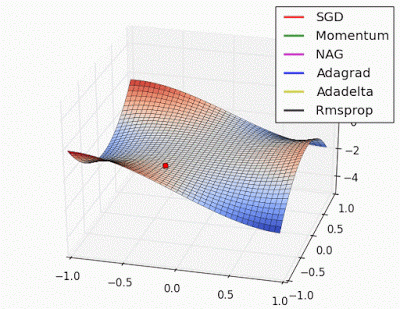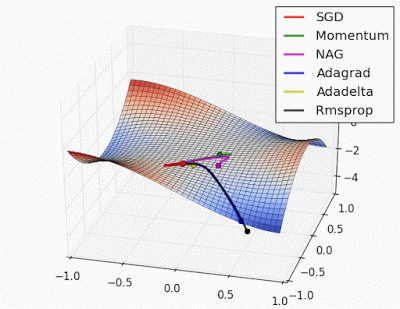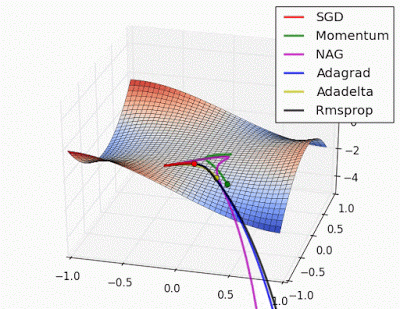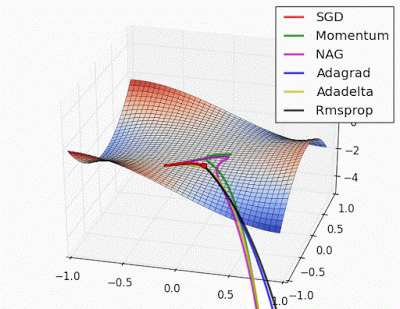
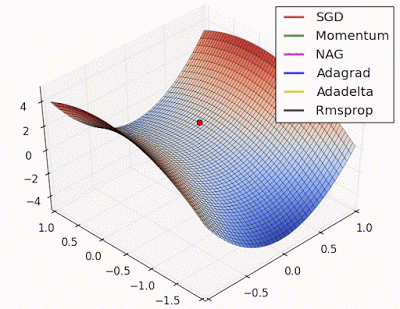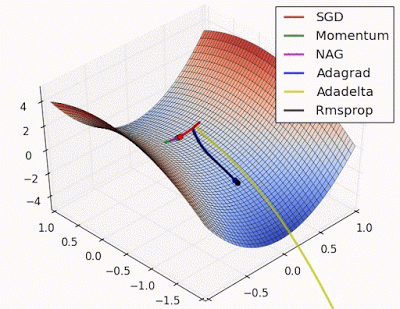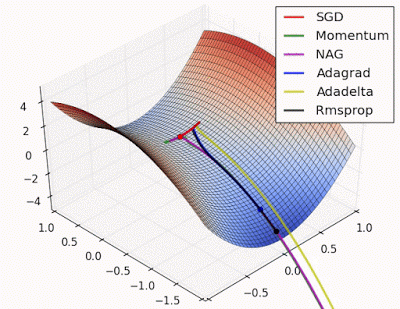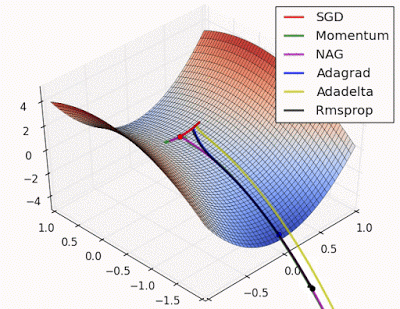
학습률 등의 하이퍼파라미터를 어떻게 설정하느냐에 따라서도 결과가 달라집니다.
즉 각각의 장단이 있어 효율적인 문제와 서툰 문제가 있습니다.
Tensorflow 등의 프레임워크에서도 한 줄만 변화시키면 쉽게 Optimizer를 바꿀 수 있으므로 다양한 시도를 통해 해결하고자하는 문제마다 최적화된 optimizer 설정이 필요합니다.