X라는 입력 데이터 집합에서
한 쪽은 [1,2,3..]과 같은 분포에 비해 다른 쪽은 [9000, 10000] 등의 차이가 편차가 큰 다른 범위 분포를 갖고 있다면, 비용 함수는 고른 모양이 아닌 한 쪽으로 매우 치우쳐버리게 되고 아무리 Learning Rate를 좋게 설정함에도 불구하고 학습 도중 밖으로 발산해버릴 수 있습니다.
이렇듯 입력데이터의 형태는 학습에 있어 많은 영향을 끼치게 되므로 데이터 전처리는 학습만큼 매우 중요합니다.
데이터를 전처리 (Data Preprocessing)하는 몇 가지 방법을 알아보려고 합니다
1. 평균 차감 (Mean Subtraction)
가장 흔하게 사용하는 전처리 기법으로서
입력 데이터의 모든 Feature 각각에 대해 평균값만큼 차감하는 방법으로 데이터 군집을 모든 차원에 대해 원점으로 이동하는 것을 목표로 하며,
특히 이미지 처리에 있어 계산의 간결성을 위해 모든 픽셀에서 동일한 값을 차감하는 방식으로 구현하며 python 라이브러리 numpy에서 다음과 같이 구현 가능합니다.
2. 정규화 (Normalization)
각 차원의 데이터가 동일한 범위 내의 값을 갖도록 하는 기법입니다.
일반적으로 다음 2가지 중 하나를 선택하여 구현합니다.
(1) 각 데이터값을 평균 만큼 차감하고 표준편차 값으로 나눕니다
이 때, 각 차원에 대해서 개별적으로 연산을 수행합니다
(2) 각 차원의 최소/최대값이 각각 -1/1이 되도록하는 기법입니다.
하지만 이 기법은 Scale이 다른 feature가 거의 동일한 비중으로 학습 결과에 영향을 줄 것이라는 가정하에 사용하는 것이 일반적입니다.
이미지 처리의 경우, 이미 입력 데이터의 각 픽셀값은 0~255사이의 값을 갖고 있는 경우가 대부분이기 때문에 정규화 전처리 기법을 반드시 사용해야하는 것은 아닙니다.
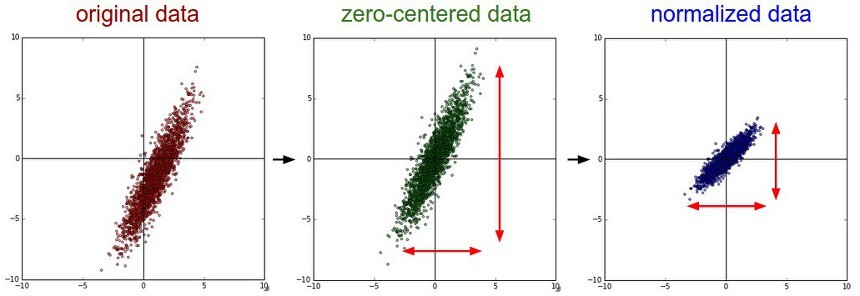
좌측 : 초기 2차원 input data
중간 : 평균차감 기법을 통한 zero-centered data
우측 : 정규화 기법을 통한 동일 범위의 데이터화. 중간 데이터에서 넓게 퍼진 y축의 데이터가 x축의 데이터 분포와 같게 변화됨
3. PCA (Principal Component Analysis)
초기 데이터 차원에서 데이터간의 상관관계 제거 및 Variance가 가능한 큰 값을 갖는 N개의 차원으로 축소시키는 기법입니다.
선형 분류기 혹은 신경망에 학습시킴으로써 좋은 성능 기대 및 트레이닝 시간과 메모리 사용 측면에서도 이점이 생깁니다.
(1) 먼저 평균차감 기법을 사용하여 초기 데이터를 정규화 시킵니다.
그리고 데이터 간의 상관관계를 나타내는 공분산(covariance)을 계산합니다.
cov matrix에서 (i, j)의 값은 X matrix에서 i, j 데이터간의 상관정도(covariance)를 나타내는 값이며 주대각선의 값들은 X matrix 각 row vector의 분산값입니다.
(2) 이어서 U행렬의 column vector는 고유벡터(eigenvector), S는 특이값(singular value)의 1차원 배열입니다.
공분산은 Symmetric, Positive-Semi-Definite의 성질이 있으므로 S벡터의 각 성분은 고유값(engienvalue)의 제곱의 값을 갖습니다.
데이터 X를 고유기저(eigenbasis)에 사상시킴으로써 데이터간의 상관관계를 제거합니다.
(3) U 행렬의 column은 norm은 1이고 서로 직교하는 orthonormal의 성질을 갖고 있기 때문에 기저벡터(base vector)가 됨을 알 수 있습니다.
따라서 고유기저로 사상하는 것은 고유벡터를 새로운 축으로하여 X데이터를 회전하는 것입니다.
Xrot행렬의 공분산을 구하면 대각행렬인 것을 알 수 있는데,
np.linalg.svd의 이점 중 하나는 U행렬의 Column vector는 각 벡터에 상응하는 고유값의 내림차순으로 정렬된다는 점입니다.
따라서 처음 몇 개의 벡터만 사용하여 데이터 차원을 축소하는데 사용할 수 있습니다
(4) 위 연산과 같이 [N*D]크기의 X데이터를 [N*100] 크기의 데이터로 압축할 수 있는데
데이터의 variance가 가능한 큰 값을 갖도록 하는 100개의 차원이 선택되어 리턴됩니다.
4. Whitening
기저벡터 데이터를 고유값으로 나누어 정규화하는 기법입니다.
PCA와 밀접하게 연관된 전처리 과정으로써 서로 작은 상관관계를 지니도록, 동일한 분산을 갖도록하여 입력값을 더 쓸모있게 만드는 작업입니다.
만약 데이터가 multivariate gaussian 분포라면 화이트닝된 데이터는 평균이 0, 공분산은 단위행렬을 갖는 정규분포를 갖게 됩니다.
식에서 분모가 0이 되는 것을 방지하기 위해 1e-5(또는 임의의 작은 상수)를 더해줍니다.
하지만 화이트닝 기법의 단점 중 하나는 모든 차원의 데이터를 동일하게 늘리게 되는데 특히 분산값이 매우 작아 노이즈로 해석할 수 있는 차원의 데이터까지 포함되어 데이터 내의 노이즈가 과장되는 현상이 나타납니다.
이러한 경우 보통 큰 수를 분모에 더하는 방식으로 노이즈 과장 현상을 완화할 수 있습니다.
좌측 : 초기 2차원 input data
중간 : PCA를 통한 zero-centered 및 공분산 행렬의 고유기저로 회전된 데이터
우측 : 화이트닝된 데이터.
Summary
CNN같은 경우에는 PCA / Whitening기법을 사용하는 경우는 거의 없지만 평균차감 및 정규화를 통한 기법은 흔히 사용하는 전처리 기법입니다.
하지만 이러한 기법을 적용함에 있어 학습 데이터만을 대상으로 식에 필요한 값을 추출해야합니다.
즉, 모든 데이터가 아닌 학습, 검증, 테스트로 나눈 후 학습 데이터만을 대상으로 평균값을 구한 후에 평균차감 전처리를 모든 데이터군에 적용해야 올바른 효과를 볼 수 있습니다.
또한 이외에도 가중치의 초깃값을 정리하는 방식과 이러한 처리에도 네트워크 내부에서 분산이 편중되어 버리므로 매 layer마다 처리를 하는 batch normalization이 있습니다.