신경망 학습에서 특히 중요한 부분 중 하나가 가중치의 초기값입니다.
잘못된 가중치를 설정한 채 학습을 시작한다면 레이어를 거듭할수록 활성화값이 부적절하거나 한 쪽에 편중되기 쉬워 신경망 학습의 성패를 가르는 일이 자주 있습니다.
아래에서는 이러한 초기화 기법들에 대해 알아보겠습니다
1. 0으로 초기화
최종적으로 학습된 신경망에서의 가중치들은 정확히 어떤 값으로 수렴해야 하는지는 알 수 없지만 데이터 정규화 기법을 적절하게 적용한 가중치의 절반은 양수, 절반은 음수 값이라는 가정을 할 수 있을 것입니다.
이에 나아가, 모든 초기 가중치를 0으로 설정함으로써 최상의 학습 결과를 얻을 수 있을 것이라는 가정 또한 합리적일 수 있습니다.
하지만 이런 경우 동일한 값을 받는 모든 뉴런들은 모두 같은 연산결과를 내보내게되고,
가중치를 수정하는 Backpropagation 과정에서 동일한 gradient 값 계산 및 동일한 값으로 업데이트가 되는 현상이 발생합니다.
즉, 가중치를 여러 개 갖는 의미를 사라지게 합니다.
뉴런들의 비대칭성을 야기할 요소가 사라지게 되므로 학습이 올바르게 진행되지 않습니다.
2. 0에 가까운 작은 난수
그렇다면 0에 충분히 가까우면서 모두 동일한 0의 값이 아닌 값을 탐색할 필요가 있습니다
즉, 모든 가중치들을 난수를 이용하여 고유한 값으로 초기화함으로써 각 파라미터 값이 서로 다른 값으로 업데이트 되고 결과적으로 전체 신경망 내에서 서로 다른 특성을 보이는 다양한 부분으로 분화되도록 도모합니다.
W = 0.01 * np.random.randn(D, H)
위와 같이 numpy 라이브러리의 randn 등의 함수를 사용하여
평균 0, 표준편차 1인 정규분포로 부터 난수를 얻어 가중치를 초기화할 수 있습니다.
정규분포가 아닌 균일분포(uniform distribution)로 부터 추출된 값은 학습된 최종 성능에 미치는 영향이 미미한 것으로 알려져 있습니다.
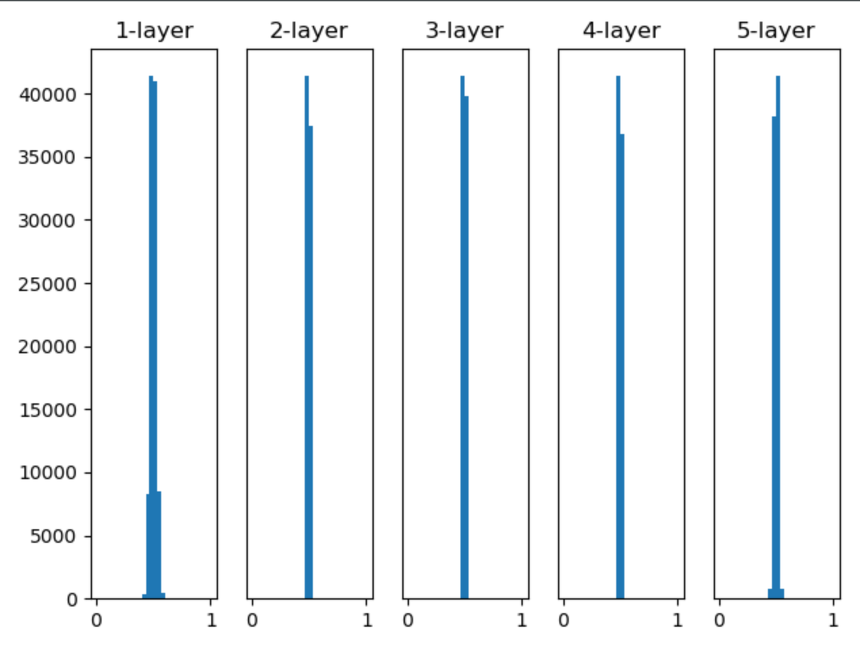
아래는 해당 초기화 방식의 각 층별 활성화 값을 시각화한 내용입니다.
활성화 값이 0.5에 치우쳐져 있는데 이는 모두 0으로 초기화하는 방식과 비슷하게 신경망의 표현력 관점에서 문제가 됩니다.
층과 층 사이에 적당하게 다양한 데이터가 흘러야 신경망 학습이 효율적으로 이뤄지기 때문입니다.
또한 해당 방식으로 나온 결과가 입력 데이터 수에 비례해서 분산이 너무 커지는 단점을 갖고 있습니다.
3. 분산보정
가중치 벡터를 입력 데이터 수(fan-in)의 제곱근 값으로 나누는 연산을 통해 뉴런 출력의 분산이 1로 정규화 할 수 있습니다.
이 방법은 근사적으로 동일한 출력분포 및 신경망의 수렴률 또한 향상시키는 것으로 알려져있습니다.
위 방식은 이와 유사한 내용의 연구로
Understanding the difficulty of training deep feedforward neural networks by Glorot et al 논문에서 설명하는 내용이며 'Xavier Initialization'이라고 부르는 방식입니다.
앞 계층의 노드가 n개라면 표준편차가 1/sqrt(n)인 분포를 사용하면 된다는 결론을 이끌었습니다.
Xavier Initialization은 활성화 함수가 선형인 것을 전제로 이끈 결과입니다.
Sigmoid, Tanh함수는 좌우 대칭이라 중앙 부근이 선형인 함수로 볼 수 있으므로 주로 사용하는 방식입니다.
해당 결과를 보면 층이 깊어지면서 형태는 다소 일그러지지만 앞선 방식보다는 확실히 넓게 분포됨을 알 수 있습니다.
이러한 일그러짐은 sigmoid함수가 아닌 tanh함수를 사용하면 개선됩니다.
W = tf.get_variable("W", shape=[fan_in, fan_out], initializar=tf.contrib.layers.xavier_initializer())
Tensorflow의 내장되어있는 함수를 사용해서 해당 방식의 초기화 또한 가능합니다.
하지만 평균이 0이라고 가정하는 것은 일반적으로 모든 상황에서 가정할 수 있는 것은 아닙니다.
ReLU 유닛의 경우만 하더라도 0보다 큰 평균값을 갖기 때문입니다.
위는 동일한 주제의 더 최근 연구로서
Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification by He et al 논문의
'He Initialization'이라는 초기화방식입니다.
해당 논문에서는 뉴런의 분산은 '2.0/n'이 되야 한다고 결론을 내리고 있으며 특히 ReLU 뉴런이 사용되는 신경망에서 권장되고 있는 방식입니다.
아마도 ReLU의 음의 영역이 0이라서 더 넓게 분포시키기 위함이 아닐까 싶습니다.
<std=0.01 정규분포>
std=0.01의 경우는 각 층의 활성화값이 아주 작은 값들입니다.
이는 역전파때 가중치의 기울기 역시 작아진다는 뜻이므로 학습이 거의 이루어지지 않을 것입니다.
xavier의 경우 층이 깊어지면서 치우침이 조금씩 커집니다.
이는 층이 깊어질수록 활성화값들의 치우침도 커지고 '기울기 소실'문제를 발생시킵니다.
마지막 He의 경우 모든 층에서 균일하게 분포됨을 알 수 있습니다.
이는 역전파 때도 적절한 값이 나올 것으로 알 수 있습니다.
4. 희소 초기화 (Sparse Initialization)
보정되지 않은 분산을 위한 또 다른 방법은 모든 가중치 행렬을 0으로 초기화 하는 것입니다.
이 때, 대칭성을 깨기 위해서 모든 뉴런을 고정된 숫자의 아래 단계 뉴런들과 무작위로 연결합니다.
연결하는 뉴런의 수는 대략 10개 정도입니다
5. Bias 초기화
가중치에 랜덤한 값을 설정함으로써 대칭성 문제는 해결되기 때문에 주로 bias는 0의 값으로 초기화합니다.
ReLU 연산의 비선형성에 의해서 몇몇 경우에는 0.01과 같은 작은 상수값을 사용하기도 하는데
이는 ReLU연산이 초기부터 발화되고 따라서 Gradient값이 유의미한 값을 갖고 신경망을 통해서 전달되는 것을 보장할 수 있기 때문입니다.
Summay
Sigmoid, Tanh 유닛 사용시 'Xavier Initialization' 방식을,
ReLU유닛 사용시 'He Initialization' 방식을 사용하여 변수 초기화 하는 방식이 일반적입니다.
다음은 최근에 또한 많이 사용되며 효과를 보고 있는 입력에 따른 활성화의 분포가 아닌 각 층이 활성화를 적당히 퍼트리도록 강제하는 방식인 Batch Normalization에 대해 알아보겠습니다.