논문 제목
Global Filter Networks for Image Classification (NeurIPS 2021 & TPAMI 2023)
URL: https://arxiv.org/abs/2107.00645 (NeurIPS 2021)
URL: https://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=10091201 (TPAMI 2023)
Github: https://github.com/raoyongming/GFNet
인용수 : 656회 (25.8.5 기준)

Abstract

• 비전 태스크를 위한 self-attention 및 MLP 모델의 최근 발전은 더 적은 inductive biases으로 우수한 성능을 달성할 수 있는 큰 잠재력을 보여줬음.
• 일반적으로 raw data로부터 spatial locations간의 상호작용을 학습하는 데 기반함.
• 하지만 이런 Transformer 구조는 이미지 크기가 커짐에 따라 이차복잡도-O(N^2)로 증가하여 고해상도 특징이 요구될 때 모델의 scale up에 부담으로 작용.
• 본 논문에서는 개념적으로는 간단하지만 연산적으로 효율적인 아키텍처인 Global Filter Network (GFNet)를 제시.
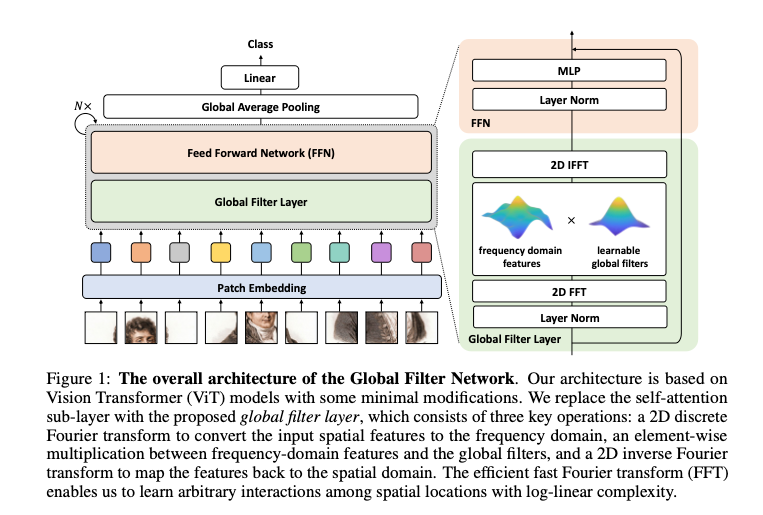
• 해당 네트워크는 주파수 영역에서 log-linear complexity로 long term spatial dependency를 학습. 트랜스포머의 셀프어텐션을 2D discrete Fourier transform, Learnable Global Filter와 2D inverse Fourier transform으로 구성됨.

Related Work

Vision transformers

이미지 분류에 트랜스포머를 도입하여 CNN 대비 경쟁력 있는 성능을 달성한 후 트랜스포머는 다양한 비전 태스크에서 잠재력을 보이기 시작했음. 최근에는 트랜스포머를 개선하려는 많은 연구들이 있었으며 더 나은 훈련 전략을 찾거나 더 나은 아키텍처를 설계 또는 두 가지 모두를 제안했음.

하지만 대부분의 트랜스포머 아키텍처 수정은 CNN과 유사한 추가적인 귀납적 편향을 도입함. 본 연구에서는 표준 트랜스포머 아키텍처에만 집중하면서 무거운 셀프 어텐션 레이어($O(L^2)$)를 CNN과 관련된 귀납적 편향을 도입하지 않으면서도 다른 공간적 상호작용을 모델링할 수 있는 효율적인 연산으로 대체하는 것이 목표라고함.

MLP-like models

최근에는 비전 트랜스포머에서 셀프 어텐션의 중요성에 의문을 제기하고 트랜스포머의 셀프 어텐션 레이어를 MLP로 대체할 것을 제안하는 여러 연구들이 있었다.

그러나 여러 연구들의 모델들은 모두 공간적으로 토큰을 믹싱하기 위해 MLP를 포함하며 이는 두 가지 단점이 있음.
1. 트랜스포머의 셀프 어텐션처럼 Spatial MLP는 여전히 토큰 길이에 대해 제곱의 연산 복잡도를 요구함.
2. 트랜스포머와 달리 공간 MLP의 가중치는 크기가 정적이여서 MLP 모델은 더 높은 해상도로 확장하기 어려움.
하지만 제안된 GFNet은 Log-Linear 복잡도를 가지며 어떤 해상도로든 쉽게 확장될 수 있다고함.

Applications of Fourier transform in vision

푸리에 변환은 수십 년 동안 디지털 이미지 처리에서 중요한 도구였음. 비전 분야에서 CNN의 획기적인 발전과 함께 비전 태스크를 위한 딥러닝 방법에 푸리에 변환을 통합하기 시작한 다양한 연구들이 있었음.
이산 푸리에 변환을 사용하여 이미지를 주파수 영역으로 변환하고, 특정 태스크에서 성능을 향상시키기 위해 주파수 정보를 활용하기도하며, 고속 푸리에 변환(FFT)을 통해 CNN을 가속화하기 위해 convolution theorem를 이용하기도 했음.

매우 최근의 연구들은 편미분 방정식을 풀거나 NLP 태스크를 해결하기 위해 푸리에 변환을 활용하여 딥러닝 모델을 개발하려고 시도하기도 했음.

해당 연구에서는 디지털 이미지 처리의 주파수 필터에서 영감을 받아서 푸리에 영역에서 토큰들 간에 전역적으로 정보를 교환하기 위해 학습 가능한 필터를 사용할 것을 제안했음. 또한 FFT의 특징을 활용하여 연산 비용과 파라미터 수를 줄임.

Method

Preliminaries: discrete Fourier transform

우선 Discrete Fourier Transform(DFT)은 디지털 신호 처리 분야에서 중요한 역할을 하며 GFNet의 핵심 구성 요소임.

먼저 1차원 DFT를 고려해보면 N개의 복소수 시퀀스 $x[n], (0≤n≤N−1)$가 주어질 때 1차원 DFT는 아래 식을 통해 시퀀스를 주파수 대역으로 변환함.

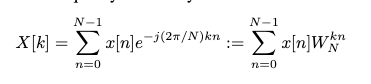
여기서 j는 허수 단위이고 $W_{N}=e^{-j(2\pi/N)}$임.
DFT 공식은 시간 영역과 주파수 영역 모두에서 샘플링함으로써 연속 신호에 대한 푸리에 변환으로부터 유도될 수 있음.

$X[k]$는 길이 N의 구간에서 반복되므로, 연속적인 N개의 지점(k=0,1,...,N−1)에서 $X[k]$가 주어지면 IDFT를 통해 원본 신호 $x[n]$을 복원할 수 있다.

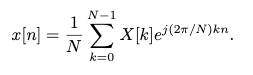
실수 입력 $x[n]$에 대해 DFT는 conjugate symmetric이라는 것을 증명할 수 있다고함. 즉 $X[N-k]=X^{*}[k]$임. 그 역도 마찬가지로 성립함.

conjugate symmetric한 $X[k]$에 IDFT를 수행하면 실수 이산 신호가 복원될 수 있다. 이는 DFT의 절반 즉 ${X[k]:0\le k\le\lceil N/2\rceil}$이 $x[n]$의 주파수 특성에 대한 모든 정보를 포함한다는 것을 의미함.

DFT는 주로 두 가지 이유로 현대 신호 처리 알고리즘에서 널리 사용됩니다
1. DFT의 입력과 출력이 모두 이산적이어서 컴퓨터로 쉽게 처리할 수 있음
2. DFT를 계산하기 위한 효율적인 알고리즘이 존재.

고속 푸리에 변환(FFT)은 $W_{N}^{kn}$의 대칭성과 주기성 속성을 활용하여 DFT 계산 복잡도를 $\mathcal{O}(N^{2})$에서 $\mathcal{O}(N \log N)$으로 줄임. DFT와 유사한 형태를 가진 IDFT 또한 IFFT를 사용하여 효율적으로 계산 가능.

앞서 설명한 이산 푸리에 변환은 2D 신호로 확장할 수 있음.
2D 신호 $x[m,n]$ (0≤m≤M−1,0≤n≤N−1)이 주어졌을 때, $x[m,n]$의 2D DFT는 다음과 같다.

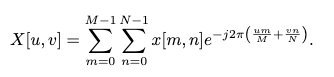
2D DFT는 두 차원에 대해 번갈아 가며 1차원 DFT를 수행한다. 1차원 DFT와 유사하게 실수 입력 $x[m,n]$의 2D DFT는 conjugate symmetric 속성 $X[M-u,N-v]= X^{*}[u,v]$를 만족함. FT 알고리즘은 2D DFT에도 적용되어 연산 효율성을 향상시킬 수 있음.

Global Filter Networks

Overall architecture

ViT의 발전으로 self-attention 기반 모델이 컨볼루션과 관련된 inductive biases 없이도 경쟁력 있는 성능을 달성할 수 있음을 보여줬음. 이로 인해 토큰 간의 정보를 혼합하기 위해 셀프 어텐션 이외의 접근 방식을 활용하는 연구가 진행되었음.
제안된 GFNet는 이러한 연구 흐름을 따르며 계산량이 많은 셀프 어텐션 레이어를 더 간단하고 효율적인 것으로 대체하는 것을 목표로 함.

모델은 H×W 크기의 패치들을 입력으로 받아서 flatten된 패치들을 차원 D를 갖는 L=HW개의 토큰으로 투영함.
GFNet의 기본 구성 블록은 다음 두 가지로 이루어진다.
1. 공간 정보를 효율적으로 (O(L log L)) 교환할 수 있는 글로벌 필터 레이어
2. FFN.
그리고 마지막 블록의 출력 토큰은 global average pooling 레이어를 거쳐 선linear classifier로 전달됨.

Global filter layer

본 논문에서는 서로 다른 spatial location을 나타내는 토큰들을 혼합할 수 있는 셀프 어텐션 레이어의 대안으로 글로벌 필터 레이어를 제안함.
토큰 $x\in\mathbb{R}^{H\times W\times D}$가 주어지면 먼저 spatial dimension을 따라 2D FFT를 수행하여 주파수 도메인으로 변환함.

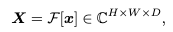
여기서 $\mathcal{F}[\cdot]$는 2D FFT를 나타냅니다. X는 복소수 텐서이며 x의 스펙트럼을 나타냄.

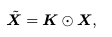
여기서 ⊙는 element-wise multiplication임. 필터 K는 X와 동일한 차원을 가지기 때문에 Global Filter라고 불리며 주파수 도메인에서 임의의 필터를 표현할 수 있다. 마지막으로 inverse FFT를 적용하여 변조된 스펙트럼 $\tilde{X}$를 다시 공간 도메인으로 변환하고 토큰을 업데이트함.

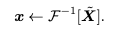
Relationship to other transformer-style models

GFNet은 토큰을 혼합하는 접근법을 따름. 비전 트랜스포머나 순수 MLP 모델과 같은 기존 아키텍처와 비교할 때 GFNet은 다음과 같은 몇 가지 유리한 속성을 가짐.

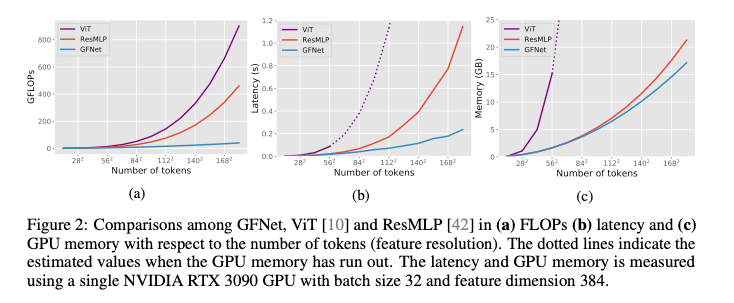
1. GFNet은 더 효율적입니다. 비전 트랜스포머와 MLP 모델의 복잡도는 모두 $O(L^2)$ 입니다. 하지만 글로벌 필터 레이어는 FFT(O(L log L)), 원소별 곱셈(O(L)) 그리고 IFFT(O(L log L))로만 구성되므로 총 계산 복잡도는$\mathcal{O}(LlogL)$이 됨.
2. 순수 MLP 모델은 트랜스포머에 비해 간단하지만 고정된 수의 토큰만 처리할 수 있기 때문에 더 높은 해상도(예: 224×224에서 384×384로)에서 fine-tuning하기 어려움. GFNet은 더 높은 해상도로 쉽게 확장될 수 있음. FFT와 IFFT 모두 학습 가능한 파라미터가 없고 임의의 길이의 시퀀스를 처리할 수 있으므로 더 유연함.

다른 입력에 대해서는 글로벌 필터 K를 목표 크기 $H^{\prime}\times W^{\prime}$에 맞춰 $K^{\prime}\in\mathbb{C}^{H^{\prime}\times W^{\prime}\times D}$로 간단히 interpolate하면 됨. 이러한 보간은 DFT의 속성 때문에 합리적이라고함.

Experiments

GFNet의 효과를 검증하기 위해 ImageNet,CIFAR-10/100, Stanford Cars, Flowers-102를 포함한 다운스트림 전이 학습 데이터셋에서 테스트를 했다고함.

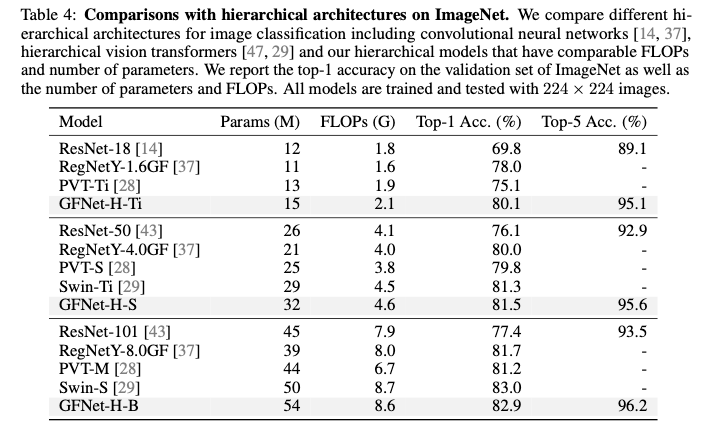
ImageNet Classification

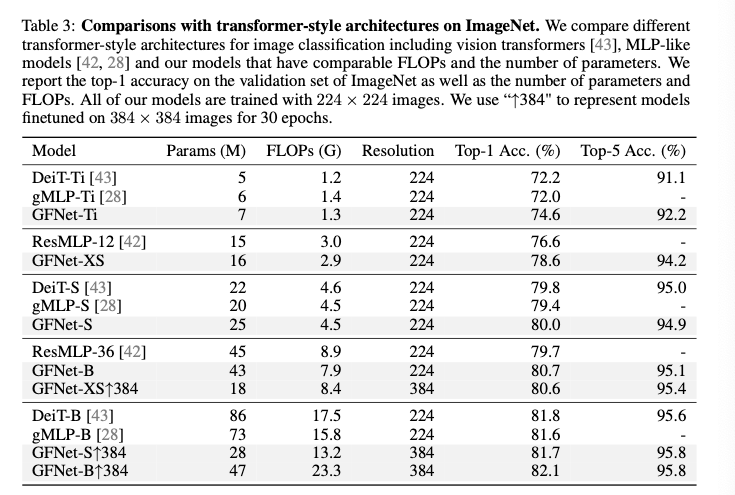
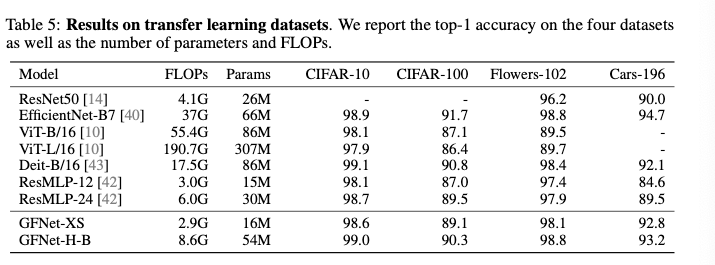
Transfer learning

일반적으로 사용되는 전이 학습 벤치마크 데이터셋에서 GFNet을 평가했다고함.

Analysis and visualization

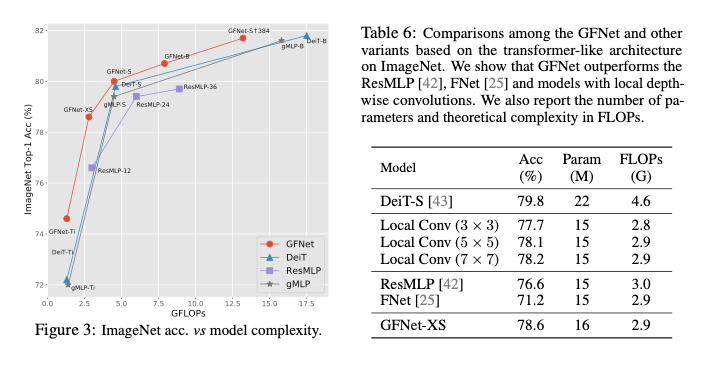
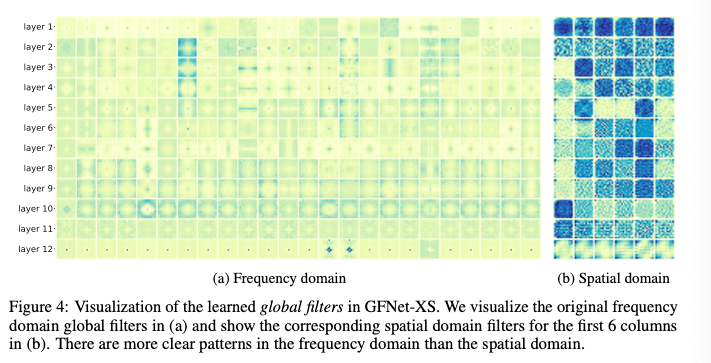
GFNet의 핵심 연산은 주파수 도메인 특징과 글로벌 필터 간의 원소별 곱셈이다. 따라서 시각화하고 해석하기가 쉬움. 그림 4에서 주파수 도메인 필터와 그에 해당하는 공간 도메인 필터를 시각화하였음. 학습된 글로벌 필터는 주파수 도메인에서 더 명확한 패턴을 가지며 레이어마다 다른 특성을 보임. 마지막 레이어의 필터는 특히 저주파수 구성 요소에 집중함. 그에 해당하는 공간 도메인 필터는 사람이 해석하기에는 덜 명확함.

Conclusion

이미지 분류를 위한, 개념적으로는 간단하면서도 계산적으로 효율적인 아키텍처인 GFNet를 제시했음. 해당 모델은 비전 트랜스포머의 셀프 어텐션 sub-layer를 2D FFT/IFFT와 주파수 도메인에서의 학습 가능한 글로벌 필터 집합으로 대체하였음. log-linear 복잡도를 가진 토큰 혼합 연산 덕분에 제안 아키텍처는 매우 효율적임. 실험 결과는 GFNet이 정확도/복잡도 트레이드오프 측면에서 비전 트랜스포머, MLP-like 모델, CNN에 대한 매우 경쟁력 있는 대안이 될 수 있음을 입증했음.