[25-1 Winter Session 6] Continuous-time Markov Chains

ESC·2025년 6월 4일

25_Winter Stochastic Process

2025-Winter

목록 보기

6/7

7.1 Introduction

마르코프 체인(Markov Chain)을 연속 시간(Continuous-Time)으로 확장

상태 간 전이 (Transition) + 각 상태에서 머무르는 시간 (Duration) 고려

중요 개념

Markov Property는 기억이 없는 특성(Memorylessness)을 가진다. 즉, 현재 상태만이 미래 상태를 결정하며, 과거 상태는 영향을 주지 않는다.
연속시간 마르코프 체인의 경우, 각 상태에서 머무르는 시간은 지수 분포(Exponential Distribution)를 따른다.
상태의 순서를 보면 이산시간 마르코프 체인(Discrete-Time Markov Chain)과 유사하지만, 머무는 시간을 고려하면 연속시간 마르코프 체인과 차이가 생김.

예제

날씨 예제

💡

Markov Transition Function

연속시간 확률 과정 $X_t$ 가 마르코프 체인이 되려면 다음을 만족해야 합니다.

즉, 미래 상태는 현재 상태에만 의존하며, 과거 상태는 영향을 주지 않는다.

연속시간 마르코프 체인은 보통 시간-동질적(Time-Homogeneous)입니다. 즉, 전이 확률이 시간에 따라 변하지 않는다는 의미입니다. 시작 시점인 s에 의존하지 않는다.

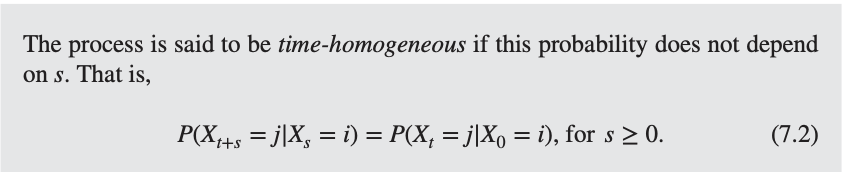
이러한 성질 덕분에 마르코프 과정의 전이 확률을 $P(t)$ 라는 transition function로 표현 가능합니다.

$P_{ij}(t) = P(X_t = j | X_0 = i)$

주의

$P(t)$ vs $\tilde{P}$

$P(t)$ : transition function
- 시간 t가 지났을 때 상태 i에서 상태 j로 도달할 확률을 나타냄
- transition matrix for a discrete-time Markov chain과 비슷한 properties를 갖는다 → Chapman-Kolmogorov Equation
$\tilde{P}$
- 단순한 상태 간 전이 확률을 나타내며, 시간 개념이 없음

💡

Chapman-Kolmogorov Equations

연속시간 마르코프 체인의 전이 확률이 어떻게 시간에 따라 연결되는지를 설명하는 핵심 방정식

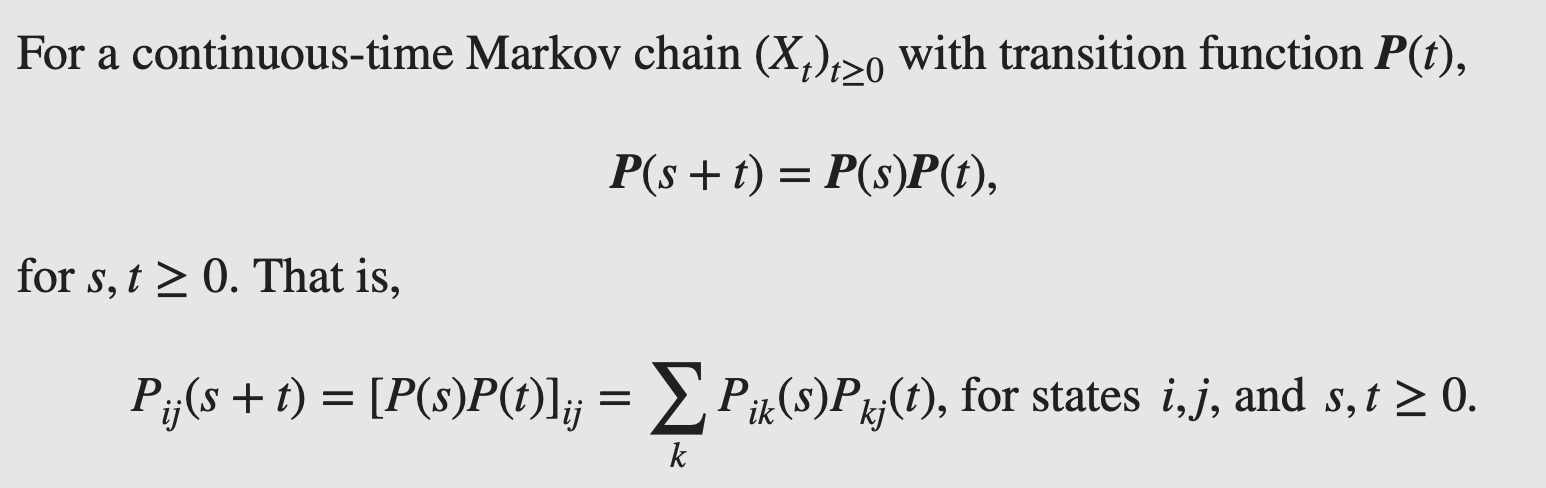
의미: 시간 s 후 상태 i에서 k로 갈 확률과, 다시 k에서 j로 갈 확률을 모두 합하면, 직접 i에서 j로 갈 확률과 동일해야 한다.

증명

Example 7.1 Poisson process

Holding Times and Embedded Chains

Time-homogeneity + Markov Property ⇒ distribution of the length of time that a continuous time chain stays in state i before transitioning to a new state

💡

Holding Times are Exponentially Distributed

$T_i$ : holding time at state i, length of time that a continuous time Markov chain started in i stays in i before transitioning to a new state
$T_i$ ~ Exponential distribution

증명

$q_i$ : 상태 $i$ 에서의 전이율

$E[T_i]=\frac{1}{q_i}$

$0<q_i<\infin$

(1) 흡수 상태 (Absorbing State)

만약 $q_i = 0$ 이라면, 해당 상태에 영원히 머무른다.
즉, 다른 상태로 절대 전이하지 않음 → Absorbing State (흡수 상태).

(2) 폭발 상태 (Explosive State)

만약 $q_i \to \infty$ 라면, 해당 상태에서 즉시 다른 상태로 전이.
즉, 도착하자마자 떠남 → Explosive State (폭발 상태).
이 경우, 무한히 많은 전이가 유한한 시간 내에 일어날 수도 있어서 비정상적인 과정.

일반적인 과정

현재 상태 $i$ 에서 머무르는 시간은 지수 분포 $\text{Exp}(q_i)$ 를 따른다.
평균적으로 $1/q_i$ 단위 시간 동안 머무른다.
다음 상태 $j$ 로 확률 $p_{ij}$ 에 따라 전이한다.
$j$ 에서 다시 머무르고, 다음 상태로 전이하는 과정이 반복됨.

즉, 각 상태에서 평균 $1/q_i$ 시간 동안 머무르고, $p_{ij}$ 확률로 다음 상태로 이동하는 과정이 무한히 반복됨.

Embedded Chain:

연속시간 마르코프 체인의 상태 전이만을 보면, 이산시간 마르코프 체인처럼 보일 수 있다.
이때 얻어지는 이산시간 마르코프 체인을 Embedded Chain (내재된 체인)이라고 부른다.
Embedded Chain의 transition matrix $\tilde{P_{ij}} = p_{ij}$ . diagonal entries: 0

7.2 Alarm clocks and transition rates

연속시간 마르코프 체인은 각 상태에서 머무르는 시간과 상태 간 전이 확률을 모두 고려해야 함.
이를 쉽게 이해하는 방법이 Exponential Alarm Clock (지수 알람 시계) 모델.

Exponential Alarm Clock

각 상태 i에서 전이할 수 있는 상태 j마다 독립적인 알람 시계가 있음.
알람 시계 (i,j)는 지수 분포를 따르는 랜덤한 시간 후에 울림.
처음 울리는 알람 시계가 다음 상태를 결정.

현재 상태 i에 도착하면, 모든 가능한 전이 (i,j)에 대해 독립적인 지수 분포 시계가 동시에 시작됨.
이 시계들은 서로 다른 속도 $q_{ij}$ 를 가지며, 각 시계는 $\text{Exp}(q_{ij})$ 분포를 따름.
가장 먼저 울리는 시계가 다음 상태를 결정.
상태가 j로 바뀌면, 다시 새로운 시계들이 동시에 시작됨.
이 과정이 계속 반복되면서 연속시간 마르코프 체인이 진행됨.

$q_{ij}$ : transition rates of the continuous time process. i→j로 가는 속도

여기서 transition rate로 알 수 있는 것: Holding Time parameters & Embedded chain transition probabilities

$q_i$

첫번째 알람이 울렸다고 하자. time of the first alarm: minimum of independent exponential random variables with parameters $q_{i1}, q_{i2}$
이 최소값은 지수 분포 $\text{Exp}(q_i)$ 를 따름

💡

여기서 $q_i = \sum_{k} q_{ik}$

즉, 상태 i에서 떠나는 총 속도는 가능한 모든 전이율의 합.

$p_{ij}$

상태 i에서 떠날 때, 다음 상태가 j일 확률은 알람 시계 (i,j)가 가장 먼저 울릴 확률과 같음.

⁍

내재된 체인(Embedded Chain)의 전이 확률은 전체 전이율 중에서 특정 전이율이 차지하는 비율.

Example 7.4

Example 7.5

7.3 Infinitesimal Generator

개요

연속시간 마르코프 체인(CTMC)에서 transition function $P(t)$ 의 변화율 = rate of change을 분석하는 것이 중요함.
이 변화율을 나타내는 행렬이 Q (무한소 생성자, Infinitesimal Generator)이다.
Q 행렬은 상태 간 전이율을 담고 있으며, 전이 확률과 직접적인 관계가 있음.

$P(t) → Q$ 유도하기

$P_{ij}(t)$

$P_{ij}(t) = P(X_t = j | X_0 = i)$ : 상태 i에서 시작하여 t 시간 후에 상태 j로 이동할 확률.
초기 상태에서 즉시 전이할 확률은 다음과 같음:

⁍

Instantaneous transition rate of hitting j if $X_t=i$

$Q$

$Q_{ii} = -q_i$
$Q_{ij} = q_{ij}$
not stochastic matrix (diag entries are negative, entries can be greater than 1, rows sum to 0)

Example 7.6

Example 7.7

$p_{ij}$ 와 $Q$ 의 관계

Embedded Chain의 전이 확률 $p_{ij}$ 은 $Q$ 를 통해 유도할 수 있음
상태 i를 떠날 때 다음 상태가 j일 확률 $(j \neq i)$

⁍

$\lim_{h\to 0^+} P(X_h = j | X_0 = i, X_h \neq i)$

조건부 분포 성질을 이용해 변형

\lim_{h\to 0^+} \frac{P(X_h = j, X_h \neq i | X_0 = i)}{P(X_h \neq i | X_0 = i)}

\lim_{h\to 0^+} \frac{P(X_h = j | X_0 = i)}{P(X_h \neq i | X_0 = i)}

💡

Instantaneous Rates, Holding Times, Transition probabilities

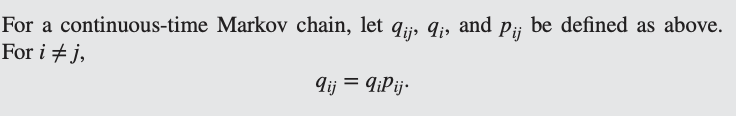
Forward, Backward Equations

$Q$ 로부터 $P(t)$ compute하기

P(t)을 시간에 따라 분석하려면,미분 방정식을 이용해야 한다.

💡

Kolmogorov Forward, Backward Equations

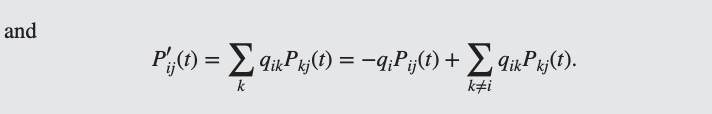
Forward: 미래의 상태 확률이 현재 상태 확률과 Q에 의해 결정됨.

Backward: 현재 상태 확률이 미래 상태 확률과 Q에 의해 결정됨.

7.4 Long Term Behavior

Reminder - Discrete Markov Chain

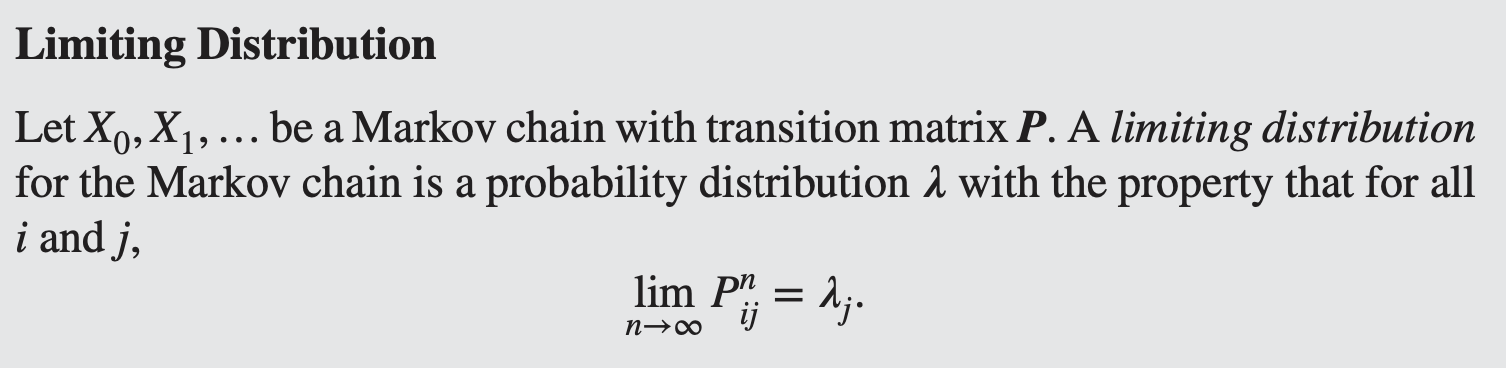
충분히 많은 단계가 지나면 ( $n \to \infty$), 어떤 상태 i에서 시작하더라도 상태 j에 있을 확률이 $\lambda_j$라는 값으로 수렴한다. 초기 상태에 의존하지 않는 장기적인 행동을 의미

Let $X_0, X_1, \dots$be a Markov chain with transition matrix $P$. 

A **limiting distribution** for the Markov chain is a probability distribution $\lambda$ with the property that for all i and j,

$$
⁍
$$

Limiting & Stationary Distribution

continuous-time markov chain에서도 discrete time markov chain과 비슷하게 limiting and stationary distribution이 정의된다.

💡

Limiting distribution

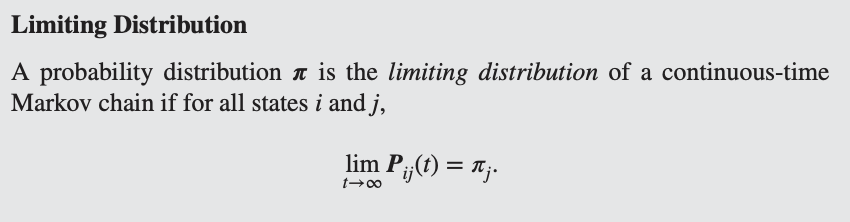
초기 상태 i가 무엇이든 간에 시간 t가 충분히 크면 상태 j에 있을 확률이 특정 값 $\pi_j$ 로 수렴해야 한다.

A probability distribution $\pi$ is the limiting distribution of a continuous-time Markov chain if for all states $i$ and $j$ ,

\lim_{t \to \infty} P_{ij}(t) = \pi_j

💡

Stationary distribution

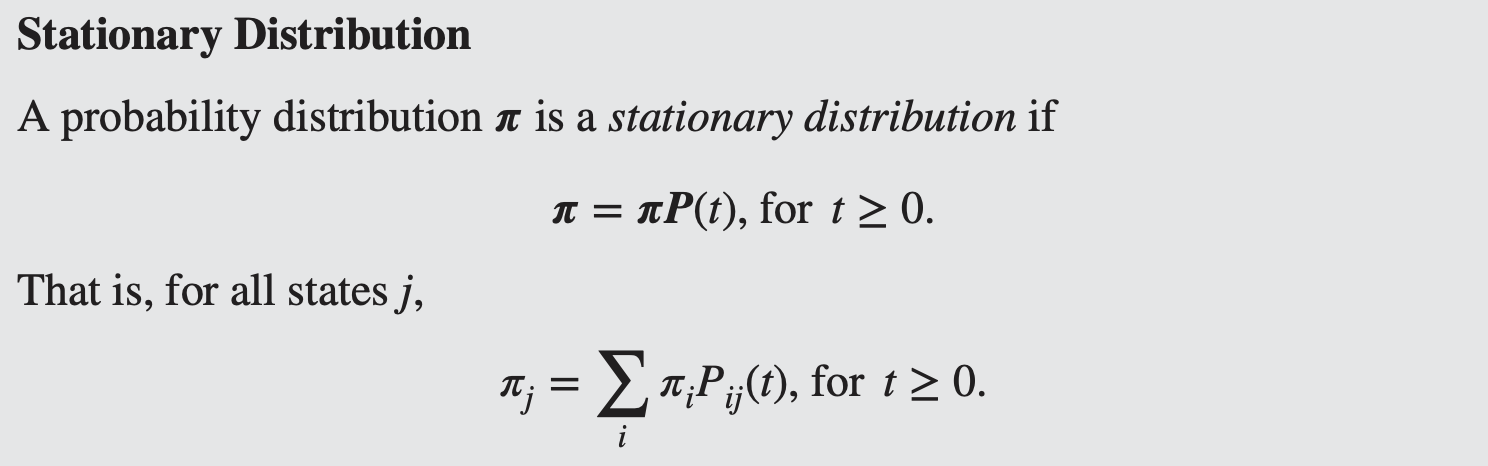
이는 특정 상태 j에 있을 확률이, 다른 모든 상태 i에서 j로 이동할 확률들의 가중합으로 나타낼 수 있어야 한다는 의미다.

limiting & stationary distribution의 관계

limiting distribution is a stationary distribution
however, converse is not necessarily true. 어떤 마르코프 연쇄에서는 정상 분포는 존재하지만, 시간이 무한히 지나도 극한 분포로 수렴하지 않을 수도 있다.

연속시간 마르코프 연쇄에서도 이산시간 마르코프 연쇄와 동일한 개념이 사용된다

accessibility: 상태 i에서 상태 j로 확률적으로 도달할 수 있는가
communication: 상태 i에서 상태 j로 도달할 수 있고, j에서 다시 i로도 도달할 수 있는가?
본질적으로 모든 state가 aperiodic
- CTMC는 시간이 연속적이므로, 특정 주기로 상태가 반복되는 구조를 갖지 않는다.
- 이산시간 마르코프 연쇄에서는 특정 시간 단계에서만 상태가 반복될 수 있지만, 연속시간에서는 임의의 시간 t에서 전이(transition)가 발생할 수 있기 때문에 주기성(periodicity)이 존재하지 않는다.
  💡
  Lemma 7.1이 그 핵심적인 이론적 근거가 된다
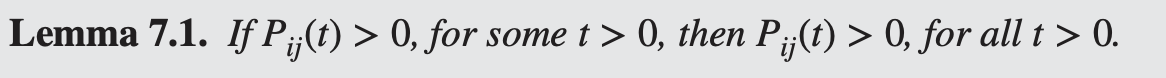
연속시간 마르코프 연쇄(CTMC)에서 한 상태에서 다른 상태로 도달할 확률 $P_{ij}(t)$ 이 한 번이라도 양수이면, 이후 모든 $t > 0$ 에 대해 양수임을 의미. 특정 ij

직관적인 인해
- 만약 $P_{ij}(t) > 0$ 인 t가 존재한다면, i에서 j로 가는 경로가 존재한다는 의미다. embedded chain에서 일정한 시간 내에 i에서 j로 도달할 수 있는 가능성이 있다는 의미
- 그러면 그 경로를 여러 번 반복할 수 있으며, 이후의 어떤 t에서도 도달 가능성이 0이 될 수 없다.
- 결과적으로 $P_{ij}(t)$ 가 한 번이라도 양수이면, 이후 모든 t>0에서도 양수가 된다.
- 즉, 이산시간 마르코프 연쇄에서 주기성이 발생하는 이유는 특정한 시간 간격에서만 상태로 돌아올 수 있기 때문이다. 그러나 연속시간 마르코프 연쇄에서는 한 번이라도 두 상태 간의 전이가 가능하면, 이후 모든 t>0에서 전이가 가능하다. 따라서 특정한 시간 간격(주기)으로만 상태가 반복되는 구조가 존재할 수 없다. 결과적으로 모든 상태가 본질적으로 비주기적(aperiodic)임을 보장할 수 있다.
irreducibility: 모든 상태가 서로 도달 가능
- 연속시간 마르코프 연쇄가 irreducible하려면, 모든 상태 $i, j$ 에 대해 어떤 $t > 0$ 에 대해 $P_{ij}(t) > 0$ 이어야 한다. 즉, 어느 상태에서든지 다른 상태로 이동할 가능성이 있다면 irreducible이라고 본다.
- 연속시간 마르코프 연쇄에서 모든 holding time parameter( $=q_i$ )이 유한하다면, 다음 두 가지 경우 중 하나가 성립한다.
1. 연쇄가 불기약(irreducible)하며, 모든 상태가 서로 연결됨 (모든 $q_i >0$ )
  
  → 즉, $P_{ij}(t) > 0$ for all i,j and t>0
  
  → 따라서 어떤 상태에서든 다른 상태로 이동할 확률이 항상 존재한다.
2. 흡수 상태(absorbing state)가 하나 이상 존재하는 경우 ( $q_i=0$ )
  
  → 이 경우 특정 상태로 이동하면 다시는 빠져나올 수 없다

Fundamental Limit Theorem

💡

Fundamental Limit Theorem

ergodic markov chain 복습

사실상 ergodic markov chain의 continuous time 버전

Let $(X_t)_{t \geq 0}$ be a finite, irreducible, continuous-time Markov chain with transition function $P(t)$ . Then, there exists a unique stationary distribution $\pi$ , which is the limiting distribution. That is, for all $j$ ,

$\lim_{t \to \infty} P_{ij}(t) = \pi_j, \quad \text{for all initial } i$

Equivalently,

$\lim_{t \to \infty} P(t) = \Pi$

where $\Pi$ is a matrix all of whose rows are equal to $\pi$ .

Stationary Distribution and Generator Matrix의 관계

💡

Stationary Distribution and Generator Matrix

증명

이해

즉, $\pi_j$ 는 시스템이 상태 j에 머무르는 평균적인 비율이다.
이는 이산시간 마르코프 연쇄에서 정상 분포가 "각 상태로의 전이 비율"을 나타내는 것과 유사하다.

(2) 왜 $\pi Q = 0$ 인가?

Q는 각 상태에서 다른 상태로 이동하는 속도를 나타내는 행렬이다.
정상 상태에서는 각 상태에서 나가는 전이율과 들어오는 전이율이 같아야 하므로 $\pi Q = 0$ 이 성립한다.
즉, πQ 방정식은 시스템이 균형 상태에 도달했을 때, 순수한 변화가 없다는 것을 의미한다.

→ 설명

예제 Example 7.14

Eat, play, sleep

Absorbing state & mean time until absorption

absorbing state가 존재하는 경우, 시스템이 흡수 상태로 도달하는 데 걸리는 평균 시간을 구하는 방법을 설명

transient state에서 시작해서 gets absorbed and never returns to that state할 확률이 있음.

$a_i$ : expected time until absorption

예시: absorbing continuous-time Markov chain on {1,…,k}. 이때 one absorbing state

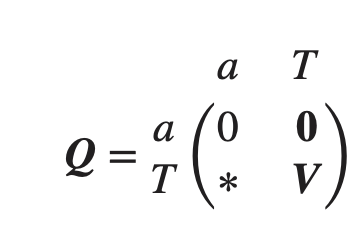
a: 흡수 상태에서 나가는 확률은 없으므로 0.
∗: transient state에서 absorbing state로 이동하는 속도
V: transient → transient 로 이동하는 속도
- (k-1) x (k-1) matrix

💡

Mean time until absorption

V는 transient 상태들 사이에서 전이율을 나타내므로, 이 행렬의 역행렬을 취하면 각 상태에서 보내는 평균 시간이 된다. 음수 부호는 전이율이 음수로 표현되기 때문

증명

예시

이 예제는 연속시간 마르코프 체인(CTMC) 을 이용하여 질병의 진행 과정을 모델링하는 방법을 설명합니다.

1. 모델 개요

다중 상태 마르코프 모델(multistate Markov model) 은 환자가 병의 여러 단계(상태)를 거쳐 진행하거나 회복하는 과정을 설명하는 데 사용됩니다.
특히, 환자가 특정 말기 상태(terminal state) 에 도달할 수 있으며, 이 상태는 흡수 상태(absorbing state) 로 간주됩니다.