[Week 2] Gradient Descent & Newton's Method

_*세션 교재: Convex Optimization - Boyd and Vandenberghe. ch.9.

1. Unconstrained Minimization Problems

이번 포스트는 아래와 같은 optimization problem을 푸는 방법에 대해 다룬다.

이때 우리는 $f : \mathbf{R^n} \rightarrow \mathbf{R}$ 가 convex이고, twice continuously differentiable (따라서 $\mathbf{dom}f$가 열려있다)인 상황에 관심이 있으며, 해를 구할 수 있는 상황, 즉 최적점인 $x^*$가 유일하게 존재함을 가정한다. 이 최적점을 $p^*= \mathbf{inf}_x~f(x)$로 표기한다.

$f$가 모든 점에서 미분 가능하고 convex하므로 $x^*$가 optimal point일 필요충분조건은 다음과 같다.

즉 주어진 제약조건이 없는 최소화 문제를 푼다는 것은 위의 식을 푸는 (미분값이 0이 되는 점을 찾는) 것과 같으며 대부분의 경우 minimizing sequence $x^{(0)}, \ x^{(1)},... \in \mathbf{dom}~f$들을 연속적으로 계산하는, 아래와 같은 iterative algorithm을 사용한다. 이러한 알고리즘은 설정된 tolerance인 $\epsilon >0$에 대해 $f(x^{(k)})-p^* \leq 0$이 만족될 때까지 $x^{(k)}$를 갱신한다.

포스트를 통해 다룰 방법론은 적절한 시작점 $x^{(0)}$을 찾는 것을 목표로 한다. 당연히 $x^{(0)}\in \mathbf{dom}~f$을 만족해야한다. 다른 말로 sublevel set인 $S=\{x\ |\ f(x)\leq f(x^{(0)})\}$가 닫혀있어야 한다. 이때 $\mathbf{dom}~f=R^n$ 또는 $f(x)~\rightarrow \infin~\ \mathsf{as}~\ x~\rightarrow~\mathbf{bd \ dom}~f$인 모든 연속 함수 $f$는 이를 만족한다.

수식으로 보면 어려워보일지 몰라도, 생각해보면 (다른 모든 점들과 마찬가지로) initial point가 domain 내에 속해야한다는 당연한 소리이다. Optimization problem에 따른 initial point의 각기 다른 조건과 관련된 두 가지 예시를 통해 이를 받아들여보자.

위와 같은 최소화 문제를 풀기 위해 목적 함수를 $x$에 대해 미분한 결과는 다음과 같다.

이는 일반적으로 analytical solution을 갖지 않으므로, iterative algorithm을 사용할 필요가 있다. 이때 $\mathbf{dom}~f=R^n$이므로, 해당 문제에 대해서는 어떤 점이라도 initial point인 $x^{(0)}$로 선택될 수 있다. 이번에는 조금 다른 최소화 문제를 생각해보자.

이 문제의 domain이 open set인 $\mathbf{dom}\ f= \{ x \ | \ a_i^Tx<b_i, \ i=1, ..., m \}$으로 주어졌을 때, 목적 함수 $f$를 $a_i^Tx \leq b_i$에 대한 logarithmic barrier라고 부르며 그 해를 (존재할 경우) inequalities에 대한 analytic center라 한다. 이때 initial point $x^{(0)}$는 반드시 $a_i^Tx<b_i, \ i=1, ..., m$을 만족해야 한다.

---

2. Strong convexity and implications

우리는 포스트의 전반에서 objective function이 strongly convex인 상황을 가정한다. 달리 말하면, 모든 $x \in S$에 대해 $\nabla^2f(x)\succeq mI$를 만족하는 어떤 $m>0$가 존재해야 한다. Strong convexity에 의해 몇 가지 흥미로운 결과가 도출된다.

위는 함수 $f$의 2차 테일러 근사이다. Strong convexity를 가정했으므로, 가장 마지막 항의 최솟값은 $(m/2)||y-x||^2_2$이다 (위의 부등식에 대입해보면 이 관계를 쉽게 도출 가능하다).

즉 위와 같은 부등식이 성립하며, 우리는 이를 suboptimality인 $f(x)-p^*$의 bound를 구하는데 사용할 수 있다. 부등식의 우변은 $y$에 대한 convex quadratic function으로, $y$에 대한 gradient를 0으로 두고 이 식의 값을 최소화하는 $y$값을 구하면 $\tilde{y}=x-(1/m) \nabla f(x)$이다. 따라서 아래와 같은 부등식의 전개가 가능하다.

해당 식은 모든 $y \in S$에 대해 성립하므로 $p^* \geq f(x)-\frac{1}{2m}||\nabla f(x)||_2^2$ 가 만족된다. 즉, 우리는 $f(x)-p^*\leq \frac{1}{2m}||\nabla f(x)||_2^2$ 를 일종의 stopping condition으로 사용할 수 있다.

이번에는 $\nabla^2f(x)$의 upperbound에 대해 생각해보자. $S$의 sublevel sets가 bounded 되어 있음은 곧 $S$가 bounded임을 의미하며, 따라서 $\nabla^2f(x)$의 maximum eigenvalue가 $S$에 바인딩된다. 정리하자면, 아래를 만족하는 어떤 상수 $M$이 존재한다.

그렇다면 위에서 정리한 것과 마찬가지로 아래의 부등식을 도출할 수 있고, 양변을 $y$에 대해 최소화한 결과는 다음과 같다.

두 개의 결과를 통합적으로 생각해보도록 하자. Strong convexity에 의해 우리는 두 개의 부등식을 도출하였고, 모든 $x \in S$에 대해 $mI\preceq \nabla^2 f(x) \preceq MI$를 만족하는 $m, M$이 존재함을 밝혔다. 이때 $\nabla^2 f(x)$는 positive definite하며, $m, M$ 각각은 $f$의 Hessian Matrix가 갖는 가장 작은 eigenvalue와 가장 큰 eigenvalue가 될 수 있다.

따라서 $\kappa=M/m$은 matrix $\nabla^2 f(x)$의 condition number에 대한 upper bound이다 (여기서 condition number란, 가장 큰 eigenvalue와 가장 작은 eigenvalue 사이의 비율이다). 이 condition number는 descent method의 수렴 속도와 관련이 있다.

이를 기하적으로 해석해보면, 우리는 convex set $C \subseteq \mathbf{R}^n$의 direction q ($||q||_2=1$)에 대한 width를 $W(C,q) = sup_{\{z\in C\}}q^Tz-inf_{\{z\in C\}}q^Tz$로 정의한다. 그리고 $C$의 minimum width와 maximum width는 각각 다음과 같다.

그리고 convex set $C$의 condition number가 어떻게 정의되는지를 보자.

둘을 연결지어 생각하면 condition number는 곧 maximum width와 minimum width 사이의 비율이 되고 (정확이 말하자면 제곱의), 따라서 set의 등방성 또는 이심률을 보여주는 지표로 사용될 수 있다. 좀 더 쉽게 얘기하면 condition number가 작을수록 set이 원에 가까운 형태를 띌 것임을 알 수 있다.

---

3. Descent methods

이제 minimizing sequence $x^{(k)}, \ k=1, ...,$ 을 계산하는 구체적인 알고리즘들에 대해 알아보자.

$\Delta x$는 step 또는 search direction으로, 어느 방향으로 이동할 지 결정하며 $t^{(k)} \geq 0$은 step size 또는 step length로 얼마만큼 이동할 지 결정한다 (물론 이 값은 $|| \Delta x^{(k)}||=1$이 아닌 이상 $||x^{(k+1)}-x^{(k)} ||$와 일치하지는 않는다). 단일 iteration에 대해서는 이를 대신하여 $x^+=x+t\Delta x,~x:=x+t\Delta x$의 노테이션을 사용하기도 한다.

여기서 descent methods란 $x^{(k)}$가 optimal일 때를 제외하고는 위의 관계를 만족하는, 즉 $k+1$번째 값이 $k$번째 값보다 무조건 작아지게끔 값을 업데이트 해가는 방법이다. 이는 모든 $k$에 대해 $x^{(k)} \in \mathbf{dom} \ f$가 성립함을 보장하며, convexity에 의해 $\nabla f(x^{(k)})^T(y-x^{(k)})\geq 0$가 $f(y) \geq f(x^{(k)})$를 의미함을 고려했을 때 descent method의 search direction은 아래를 만족해야 한다.

이를 만족하는 search direction을 descent direction이라고 부른다. 다음은 General Descent Method의 기본적인 진행 순서이다. 첫째, descent direction $\Delta x$를 정하고, 둘째, step size $t$를 고르는 작업이 설정한 stopping criterion을 만족할 때까지 반복된다.

Algorithm General descent method
$\mathbf{given}$ a starting point $x \in \mathbf{dom} \ f$
$\mathbf{repeat}$
1. Determine a descent direction $\Delta x$
2. Line search. Choose a step size $t>0$
3. Update. $x := x+t \Delta x$
$\mathbf{until}$ stopping criterion is satisfied ($||\Delta f(x)||_2\leq \eta$, for example)

여기서 두 번째 단계인 Line search는 Descent Method에서 step size $t$를 설정하는 방법 중 하나로, line인 $\{ x+t \Delta x \ | \ t \in R_+\}$의 어디에 다음 iterate가 위치할지를 $t$가 결정하기 때문에 이렇게 이름 붙여졌다. Step size가 너무 크면 최적점으로 수렴하지 않을 수 있고, 반대로 너무 작으면 최적점에 수렴하는 속도가 느려지므로, 이러한 방법을 이용하여 적절한 step size를 찾는 것이 중요하다.

(1) Exact line search

첫 번째 방법인 Exact line search는 $\{ x+t \Delta x \ | \ t \geq 0 \}$ 위에서 $f$를 최소화하는 $t$를 찾아 이를 step size로 설정한다.

다만 이러한 방식은 매 스텝마다 위의 $\argmin$ 값을 구해야 하기 때문에 효율적이지는 못하다.

(2) Backtracking line search

이런 비효율성을 완화하기 위해, 실제로 사용되는 대부분의 line search는 ‘대략적으로’ 혹은 ‘적당히’ $f$를 줄이는 것을 목표로 한다. 이를 실현하는 방법 중 하나인 backtracking line search는 매우 간단하며 상당히 효율적이다.

Algorithm Backtracking line search
$\mathbf{given}$ a descent direction $\Delta x$ for $f$ at $x \in \mathbf{dom} \ f, \alpha\in(0,0.5),~\beta\in(0,1)$.
$t:=1$
$\mathbf{while}$ $f(x+t\Delta x)>f(x)+\alpha t \nabla f(x)^T\Delta x,~~t:=\beta t$

해당 알고리즘이 ‘backtracking’이라고 불리는 것은, 하나의 step을 가보고 ($t:=1$), 해당 step에서 너무 많이 이동했다면 step size를 줄여서 ($t:= \beta t$) 다시 이동하는 과정을 반복하며 $t$를 찾기 때문이다.

---

4. Gradient Descent methods

지금까지는 제약이 없는 최적화 문제를 풀기 위한 iterative method의 기본적인 아이디어와 그 필요성 등 기초적인 내용들을 다뤄보았다. 이제부터 본격적으로 이 방법론 중 하나인 Gradient Descent Methods에 대해 이야기 해보도록 하자.

우선 머릿속에 $y=x^2$라는 가장 간단한 형태의 이차함수 그래프를 떠올려보라. 우리는 시작점 $x_0$을 optimal point인 $x=0$을 기준으로 왼쪽에 잡게 될수도, 오른쪽에 잡을 수도 있다. 만약 전자처럼 $x$가 커질수록 함숫값이 작아지는 중이라면, 즉 기울기의 부호가 음수라면 최솟값에 도달하기 위해서는 양의 방향으로 $x$를 옮겨야 한다. 반대로 후자의 경우처럼 $x$가 커질수록 함숫값이 커지는, 기울기의 부호가 양수인 경우라면 음의 방향으로 $x$를 옮기면 된다. 이러한 논리를 수식으로 표현해보면 ‘$x_{i+1}=x_i -$ (이동 거리)$\times$(기울기의 부호)’와 같이 표현될 수 있다.

그렇다면 이동 거리는 어떻게 구해야 할까? 중요한 사실이 하나 있다. Gradient는 극솟값에 가까울수록 그 값이 작아진다. 따라서 이동거리를 gradient의 크기와 비례하게 설정하여 사용한다면, 현재 $x_k$값이 극솟값에서 멀 때는 많이 이동하고, 가까울 때는 조금씩 이동할 수 있게 된다. 그렇기에 이동거리로 gradient의 값을 직접 이용하되, 이동거리를 사용자가 적절하게 조절할 수 있게끔 step size인 $\alpha$값을 추가해주면 된다. 결과적으로 ‘$x^{(k+1)}=x^{(k)}+\alpha_k \nabla f(x_i)$’라는 식이 도출되는 것이다.

정리하자면 가장 자연스러운 search direction은 negative gradient인 $\Delta x = - \nabla f(x)$이다. 이를 기반으로한 알고리즘을 gradient algorithm, 또는 gradient descent algorithm이라고 부른다. 이 컨셉을 참고 교재의 표현에 맞게 정리해보자.

Algorithm General descent method
$\mathbf{given}$ a starting point $x \in \mathbf{dom} \ f$
$\mathbf{repeat}$
1. $\Delta x := - \nabla f(x)$
2. Line search. Choose a step size $t$ via exact or backtracking line search
3. Update. $x := x+t \Delta x$

위에서도 잠시 언급됐지만, 일반적으로 stopping criterion은 $|| \nabla f(x)||_2 \leq \epsilon$의 형태를 띈다. 대부분의 경우 update 이후보다는 step 1 직후에 만족 여부가 확인된다.

---

5. Convergence analysis for exact line search

이번에는 gradient method를 위한 simple convergence analysis를 살펴보자. 본격적인 증명에 앞서 거쳐야 할 몇 가지 준비사항이 있다. 우선 표현의 단순화를 위해 $x^{(k+1)}=x^{(k)}+t^{(k)}\Delta x^{(k)}$는 $x^+=x+t\Delta x$로 대체한다. 이때 $f$는 $S$에서 strongly convex하기 때문에 모든 $x \in S$에 대해 $mI\leq \nabla^2 f(x) \leq MI$를 만족하는 positive constant $m$과 $M$이 존재한다. 또, 포스트의 앞 부분에서 $\nabla ^2f$의 upperbound에 대해 논할 때 $f(y)\leq f(x)+\nabla f(x)^T(y-x)+\frac{M}{2}||y-x||_2^2$ 라는 식을 도출했었고, 약간의 식 조작을 거쳐 $p^*\leq f(x)-\frac{1}{2M}||\nabla f(x)||_2^2$를 얻었다. 이 ‘준비물’들을 아래와 같이 넘버링한다.

이제 함수 $\tilde f(t) = f(x-t\nabla f(x))$를 정의하자. 첫번째로, $(2)$식의 $y$자리에 $x-t \nabla f(x)$를 대입하면 아래와 같이 정리된다. 복습하자면 exact line search에서 $t=\argmin_{t>0}~f(x+t\Delta x)$ 였고, gradient descent에서 $\Delta x=-\nabla f(x)$이다. 이를 통해 $\tilde{f}$의 quadratic upper bound를 구할 수 있다.

위 식의 우변은 simple quadratic으로 $t=1/M$에서 최솟값을 갖고, 그때의 minimum value는 $f(x)-(1/(2M)) || \nabla f(x)||^2_2$ 이다. 이때 $t_{exact}$가 $f(x)$를 최소화하는 step length라면, exact line search를 통해 찾은 가장 최적의 $t_{exact}$를 대입 : 즉 새로운 $x^+$를 가장 잘 업데이트 해도 위의 식이 성립한다. 이를 정리해보자.

아래는 바로 위 식의 양변에서 optimal value $p^*$를 빼주고, 우변의 $f(x)-p^*$를 식 $(3)$을 이용해 정리해주는 과정이다.

이때 $c=(1- \frac{m}{M})$로 두고 $k^{th}$ iteration에 대해 생각하면 아래의 식이 나온다.

당연히 $c$는 1보다 작으므로 우변이 결국 수렴함을 알 수 있고, $\frac{m}{M}$의 값은 앞서 다룬 condition number와 관련이 있을 것이다. Condition number의 upperbound는 $\frac{M}{m}$이고, $\frac{M}{m}$이 작으면 그 역수인 $\frac{m}{M}$은 커져 $c=1-\frac{m}{M}$은 작아진다. 따라서, condition number가 작을수록 optimal point로 더 빠르게 수렴함을 당연하게 받아들일 수 있다. 본 포스트에서는 다루지 않지만, 비슷한 흐름을 통해 backtracking line search의 convergence 역시 보일 수 있다.

---

6. Steepest descent method

$f(x+v)$ around $x$의 1차 테일러 근사는 아래와 같다.

이때, 우변의 $\nabla f(x)^Tv$는 $f$에 대한 $x$에서의 $v$ 방향 directional derivative이다 (directional derivative의 개념에 대한 내용은 다른 포스트인 Subgradient(2)의 하단에서 확인할 수 있다). 아주 작은 step $v$에 대해서 위의 식이 성립하므로 $v$의 크기를 적절히 제한하고 방향을 결정해야 한다. 만약 이 ‘방향 도함수’ 값이 음수라면, step $v$는 descent direction이 된다.

이제 $|| \cdot ||$를 $\mathbf{R}^n$의 norm이라고 하자. 우리는 Normalized steepest descent direction을 아래와 같이 정의한다.

이때의 $v$는 $f(x)$의 1차 근사식을 가장 빨리 감소시키는 방향이다. 즉 $\nabla f(x)^Tv$을 최소화하는 $v$를 찾아 search direction으로 정하는 것이며, $||v||=1$로 제한을 주어 $\argmin$의 값이 $- \infin$이 되지 않도록 신경써준다. Euclidean norm, quadratic norm과 같이 기준이 되는 norm은 별도로 설정해준다.

Algorithm Steepest descent method
$\mathbf{given}$ a starting point $x \in \mathbf{dom} \ f$
$\mathbf{repeat}$
1. Compute steepest descent direction $\Delta x_{sd}$
2. Line search. Choose $t$ via exact or backtracking line search
3. Update. $x := x+t \Delta x_{sd}$
$\mathbf{until}$ stopping criterion is satisfied

이때 Steepest descent direction인 $\Delta x_{sd}$는 $|| \nabla f(x) ||_* \Delta x_{nsd}$이다. 예를 들어 norm을 Euclidean norm으로 설정할 경우 Steepest descent direction이 단순히 negative gradient가 되기 때문에 ($\Delta x_{sd} = -\nabla f(x)$) 앞서 다룬 gradient method와 동일해진다.

이번에는 위와 같이 정의되는 Quadratic norm의 경우에 대해 생각해보자. 이러한 경우 $\Delta x_{nsd} = \argmin\{\nabla f(x)^T v~|~||v||p = (v^Tpv)^{1/2}=||p^{1/2}v||_2=1\}$로 정리된다. Duality 포스트에서 다룬 KKT condition을 이용하여 최적화 문제를 변형시켜주면 $\nabla f(x)+\lambda(2Pv)=0$이 도출되고, 따라서 $v\propto -P^{-1}\nabla f(x)$의 관계를 얻을 수 있다.

Quadratic norm $|| \cdot ||_ \mathbf{p}$에서의 Steepest descent method 결과가 갖는 의미에 대해 조금 더 생각해보자. $\bar{u}=P^{1/2} u$, 즉 $||u||_P=||\bar{u}||_2$인 상황을 정의한다면, original problem $f$에 대한 minimization을 equivalent한 problem인 $\bar{f}: \mathbf{R}^n \rightarrow \mathbf{R}$의 minimization으로 변환할 수 있다.

이때 $\bar{f}$에 gradient method를 적용하면 $\bar{x}$에서의 search direction은 아래와 같아진다.

위의 gradient search direction은 다음의 direction과 일치한다.

정리하자면 이는 $\bar{x}=P^{1/2}x$을 통해 좌표변환을 수행한 후 gradient method를 적용한 결과와 같다.

위는 알고리즘을 수행한 결과이다. 첫번째 그림은 condition number가 작아져 수렴 속도 역시 빨라진 상황을, 두번째 그림은 condition number가 커져서 수렴 속도가 느려진 상황을 나타낸다. 이처럼 Quadratic norm을 정의하는 행렬 P를 잘 선택하면, condition number를 줄여 convergence 속도를 빠르게 할 수 있다.

---

7. The Newton step

이번에는 또 다른 iterative method인 Newton’s Method에 대해 알아보자. $x \in \mathbf{dom}f$에 대해 Newton step은 다음과 같이 계산된다.

Hessian인 $\nabla^2f(x)$의 Positive definiteness는 $\nabla f(x)=0$이 아닌 한 다음이 만족됨을 보장한다.

따라서 gradient descent와 마찬가지로 Newton step은 descent direction이며, 둘의 iteration 식을 비교해보면 아래와 같다.

Gradient Descent

$x^{(k)}=x^{(k-1)}-t_k \cdot\nabla f(x^{(k-1)}),~k=1,2,3,...$

Newton’s Method

$x^{(k)}=x^{(k-1)}-(\nabla^2f(x^{(k-1)})^{-1}\nabla f(x^{(k-1)}),~k=1,2,3,..$

이 Newton step이 도출되는 과정과 그에 대한 해석을 몇 가지 살펴보도록 하자.

(1) Minimizer of second-order approximation

$\hat{f}$에 대한 second-order Taylor approximation은 위와 같은 convex quadratic function이며, $v= \Delta x_\mathsf{nt}$에서 최소화된다. 즉 second-order approximation을 최소화하기 위해서 $x$에 더해져야 하는 것은 Newton step인 $\Delta x_\mathsf{nt}$이다.

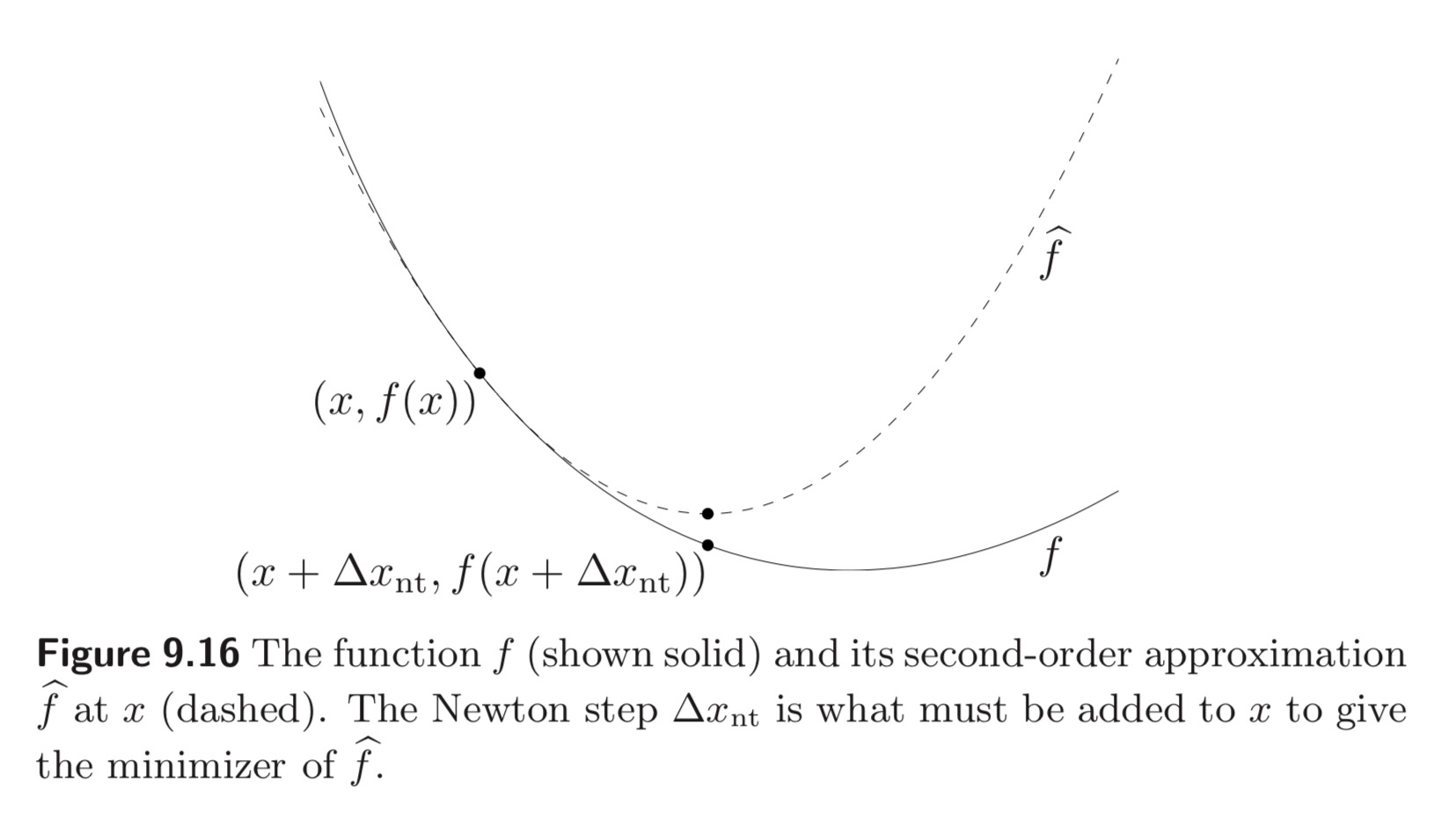
이와 같은 해석은 Newton step에 대한 인사이트를 제공한다. 만약 함수 $f$가 quadratic이라면, $x+ \Delta x_\mathsf{nt}$는 $f$의 exact minimizer이다. 그리고 $f$가 nearly quadratic이면 $x+ \Delta x_ \mathsf{nt}$는 $f$의 minimizer인 $x^*$의 아주 좋은 estimate가 된다. Twice differentiable한 함수 $f$에 대해서 $x$가 $x^*$의 근처에 있다면 이러한 $x$에서 quadratic model의 정확도가 높을 것이고, 따라서 $x+ \Delta x_\mathsf{nt}$가 좋은 추정값이 된다.

(2) Solution of linearized optimality condition

$x$의 근처에서 optimality condition인 $\nabla f(x^*)=0$을 linearize하면 $v$에 대한 선형 방정식인 아래의 식을 얻을 수 있으며, 그 해는 $\Delta x_\mathsf{nt}$이다.

따라서 Newton step $\Delta x_\mathsf{nt}$는 ($x$가 $x^$ 근처에 있어 optimality condition이 성립해야 할 때*) linearized optimality condition이 성립하기 위해서 $x$에 더해져야 하는 값이다.

(3) Steepest descent direction in Hessian norm

마지막으로 Newton step은 Hessian $\nabla ^2 f(x)$에 의해 정의된 quadratic norm이 아래와 같이 주어졌을 때 $x$에서의 steepest descent direction이다.

이는 Newton step이 (특히 $x^$ 근처의 $x$에서) 매우 좋은 search direction* 이라는 사실에 대한 또 다른 직관을 제공할 수 있다.

이러한 Newton step의 중요한 특징은 linear한 (또는 affine) 좌표 변환에 독립적이라는 사실이다. Nonsingular matrix $T \in \mathbf{R}^{n\times n}$에 대해 $\bar{f}(y)=f(Ty)$를 정의하자. 그렇다면 $x=Ty$에 대해 아래의 관계식을 도출할 수 있다.

따라서 $\bar{f}$에 대한 $y$에서의 Newton step은 다음과 같다.

이때 $\Delta x_ \mathsf{nt}$는 $f$의 $x$에서의 Newton step이며, 따라서 $f$와 $\bar{f}$의 관계는 아래와 같이 정리된다.

다음으로 현재 위치한 $x$가 optimal point인 $x^*$와 얼마나 가까운지를 나타내는 지표로서 Newton decrement를 사용할 수 있고, 이는 stopping criterion으로 기능하기도 한다.

$\hat{f}$의 quadratic approximation인 $f(x)-\inf_y~\hat f(y)=\frac{1}{2}\lambda(x)^2$을 이용하면 $\lambda^2/2$가 $f(x)-p^*$의 추정값임을 보일 수 있다. 또한 Newton decrement는 아래의 형태로 표현되기도 한다.

이는 $\lambda$가 Newton step의 quadratic Hessian norm과 동일함을 시사한다. 이와 같은 Newton decrement는 backtracking line search에서도 등장하며, $f$의 $x$에서의 (Newton step 방향으로의) directional derivative으로 해석될 수 있다. 마지막으로 Newton decrement는 Newton step과 마찬가지로 affine invariant ($\bar{f}(y)=f(Ty)$)하다.

---

8. Newton’s method

이전 포스트에서 소개한 general descent method에서 Newton step을 search direction으로 사용할 때, 우리는 이를 Newton’s method (또는 damped Newton method, guarded Newton method) 라고 부른다. 다만 general descent method에서와는 달리 stopping criterion이 update 이후가 아닌 search direction 계산 직후에 확인됨에 유의하자.

Algorithm Newton’s method
$\mathbf{given}$ a starting point $x \in \mathbf{dom} \ f$, tolerance $\epsilon>0$
$\mathbf{repeat}$
1. Compute the Newton step and decrement.
$\Delta x_{nt} := -\nabla^2 f(x)^{-1}\nabla f(x); \quad \lambda^2:=\nabla f(x)^T\nabla^2f(x)^{-1}\nabla f(x)$
2. Stopping criterion. $\mathbf{quit}$ if $\lambda^2/2\leq\epsilon$
3. Line search. Choose step size $t$ by backtracking line search.
4. Update. $x:=x+t\Delta x_{nt}$

Newton’s method의 convergence를 확인하기 전에 몇 가지 기본적인 가정을 하도록 한다.

(1) $f$가 twice continuously differentiable하며, 상수 $m$에 대해 strongly convex하다. 즉, $\nabla^2 f(x) \succeq mI \ \text{for} \ x \in S$가 만족된다.

(2) $f$의 Hessian이 $S$에서 상수 $L$에 대해 Lipschitz continuous하다. 즉, $||\nabla^2f(x)-\nabla^2f(y)||_2\leq L||x-y||_2 \ \text{for all} \ x, y \in S$가 만족된다.

*이때의 $L$은 $f$가 quadratic function을 통해 얼마나 잘 approximated 되는지를 측정한다. 즉 $L$이 작다는 것은 function $f$가 quadratic한 형태에 가까움을 의미한다.

이제 Convergence proof에 대한 간단한 idea와 outline만을 제시하고자 한다. 우리는 우선 아래를 만족하는 $0< \eta \le m^2/L$와 $\gamma>0$이 존재한다는 사실을 보여야 한다.

• 만약 $||\nabla f(x)||_2\geq \eta$라면, $f(x^{(k+1)})-f(x^{(k)})\leq-\gamma$이 만족
• $||\nabla f(x)||_2<\eta$라면, backtracking line search는 $t^{(k)}=1$을 선택하며 $\frac{L}{2m^2}||\nabla f(x^{(k+1)})||_2\leq(\frac{L}{2m^2}||\nabla f(x^{(k)})||_2)^2$이 성립

첫 번째 조건의 식은 gradient의 값이 $\eta$보다 같거나 크면 다음 iteration에서의 값이 최소 $-\gamma$만큼 감소한다는 것을 의미한다. 두 번째 조건의 경우 해당 조건이 한 번 만족이 되면 이후의 iteration에 대해서는 recursive하게 만족되므로, full Newton step $t=1$이 선택됨을 의미한다. 이를 통해 stopping criterion을 $f(x)-p^*\leq \frac{1}{2m}||\nabla f(x)||_2^2$로 설정할 수 있다. 참고로 첫 번째 조건에 해당하는 단계를 damped Newton phase, 두 번째에 해당하는 단계를 quadratically convergent phase라 칭한다.

*Gradient descent에서는 $f(x^{(k)})-p^*\leq c^k(f(x^{(0)})-p^*)$ 이었다.

Damped Newton phase에서는 대부분의 iteration이 backtracking step을 요구하며, $p^*>-\infin$일 경우 해당 phase는 최대 $(f(x^{(0)})-p^*)/ \gamma$의 iteration 후에 종료된다. Quadratically convergent phase에서는 모든 iteration이 step size로 $t=1$을 사용하며, $||\nabla f(x)||_2$가 0으로 quadratically 수렴한다. ( $\frac{L}{2m^2}||\nabla f(x^{(t)})||_2\leq(\frac{L}{2m^2}||\nabla f(x^{(k)})||_2)^{2^{l-k}}\leq(\frac{1}{2})^{2^{l-k}},\ l\leq k$)

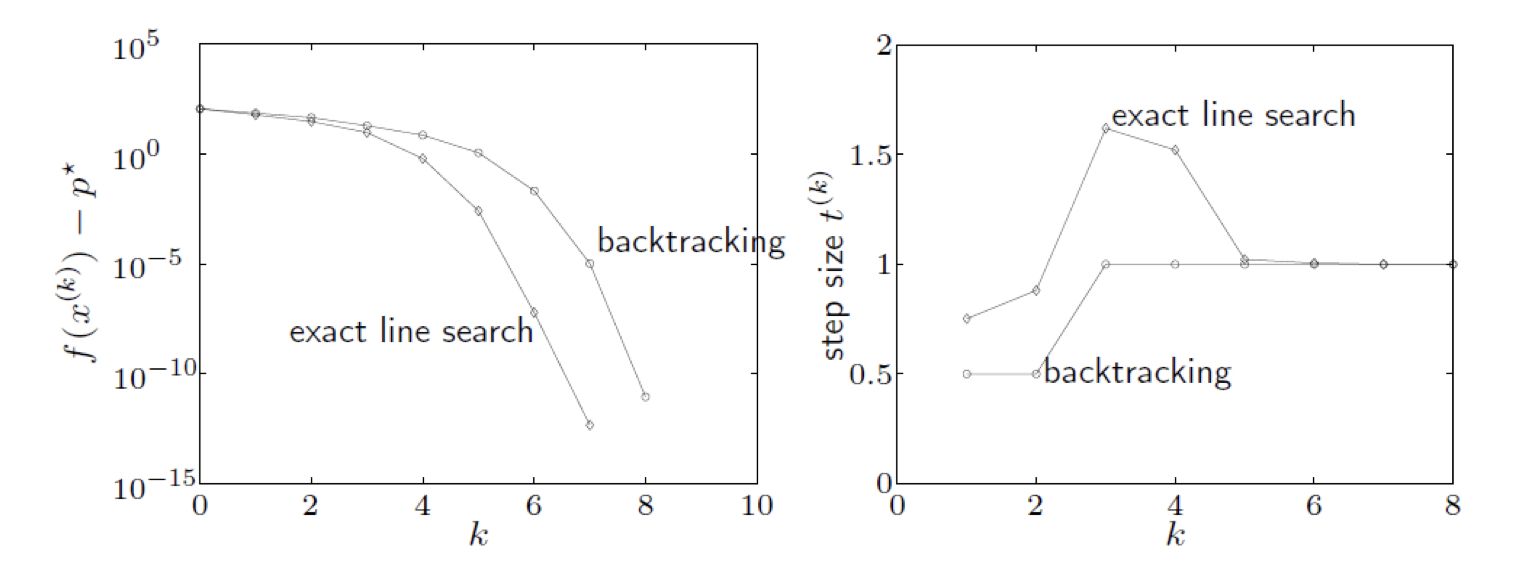
예시를 살펴보았을 때, 두 개의 line search 방법을 사용한 Newton’s method가 전부 빠르게 수렴함을 관찰할 수 있으며 step size인 $t$의 변화를 plotting 해보면 algorithm의 two phase를 분명하게 확인할 수 있다. 결론적으로, $f(x)-p^* \leq \epsilon$을 만족하기까지의 iteration 횟수는 다음의 required iteration에 bounded above 되어있다.

이때의 $\gamma$, $\epsilon_0$은 $m, L, x^{(0)}$에 의존하는 상수이다. 다만 실제로는 상수 $m, L$이 알려져있지 않은 경우가 대부분이기에 문제가 발생할 수 있다. 이를 보완하기 위해 사용하는 개념을 간단히만 소개하고 포스트를 마무리하도록 하겠다.

---

A. Self concordance

Newton’s method에는 몇 가지 shortcomings가 존재한다.

1. 미지의 상수인 $m, M, L$에 의존: 수렴성, 수렴 속도는 보일 수 있지만 해를 찾는데 얼마만큼의 Newton step이 필요한가 등의 분석이 거의 불가능함

*$m$: strong convexity lower bound, $M$: strong convexity upper bound, $L$: Lipchitz constant

1. Newton’s method 자체는 affine invariant한 반면 Convergence analysis에 있어서는 그렇지 않음: 일반적으로 좌표축의 변화에 따라 $*m, M, L*$의 값이 달라짐

*affine invariant: update의 방향이 좌표계의 affine한 변환에 대해 독립적 (=affine transformation에 대해 변환된 좌표계에서의 수렴 속도가 동일하다)

이와 같은 두 가지 단점을 보완하고자 등장한 개념이 Self-Concordant이며, 해당 개념은 다음의 3가지 이유에서 의미를 갖는다.

1. 추후 다룰 Interior-point methods에 중요한 역할을 하는 logarithmic barrier function들이 self-concordant function에 속함

*Interior-point method: 내부점 방법, KKT Conditions를 조금 수정한 식을 풀어서 점근적으로 최적해를 찾아나가는 방법

1. Self-concordant function들의 Newton’s method analysis에는 미지의 상수가 등장하지 않음
2. Self-concordance는 affine-invariant

Convex function f는 아래의 식을 만족할 때 self-concordant하다.

모든 Linear function과 Convex quadratic function를 포함한 다양한 함수들이 self-concordant함을 간단하게 보일 수 있으며, 우변의 상수 2는 편의상 채택된 것일 뿐, 2의 자리에 다른 positive constant k가 들어간 부등식이 만족되어도 self-concordant 함과 Self-concordance가 affine invariant 하다는 두 개의 성질을 유도할 수 있다.

Self-concordance를 보존하는 연산들은 다음과 같다.

• Scaling: 함수 $f$가 self-concordant 하다면, 1 이상의 상수 $a$에 대해 $af$도 self-concordant 하다.
• Sum: 함수 $f_1$과 $f_2$가 self-concordant 하다면, $f_1+f_2$ 역시 self-concordant 하다.
• Composition with affine function: 함수 f가 self-concordant 하다면, affine function $g$와의 합성 함수 $f(g(x))$역시 self-concordant 하다.
• Composition with logarithm: 다음의 합성은 self-concordance를 보존한다.

교재의 9.6장에는 $g$의 자리에 들어갈 수 있는 다양한 함수들이 소개되어 있다. 이후 교재 9.6장에서는 bound를 다룰 때 strong convexity가 아닌 Newton decrement를 이용하는 방법과 함께, strictly convex한 self-concordant function에 backtracking line seach를 이용한 Newton’s method가 어떻게 적용되는지를 다루고 있다. 이를 통해 궁극적으로는 미지의 상수인 $m, M, L$에 의존하지 않는 iteration bound를 새롭게 도출할 수 있다. 자세한 내용은 교재를 참고하라.