[Week 3] Sub-gradient Method [1]

* 세션 교재: Stanford university - EE364b - Convex Optimization II lecture notes - Stephen Boyd.

지금까지 우리는 제약 조건이 없는 Convex한 목적 함수가 모든 점에서 미분 가능하다는 전제 하에 최적화 문제를 해결하는 알고리즘들을 다루었다. 그러나 많은 현실의 문제들은 이와 같이 ‘수학적으로 예쁜’ 모양을 띄고 있지 않다. 제약 조건이 있을 수도 있고, 미분이 불가능한 점이 있을 수도 있다. 그렇다면 이와 같은 경우에는 어떻게 목적 함수를 최소화 할 수 있을까?

Sub-gradient method는 non-differentiable convex function을 최소화할 수 있게 해주는 알고리즘이다. 이는 목적 함수를 한 번 미분한 값, 즉 gradient를 이용하는 ‘first order method’에 속하며 따라서 일반적인 Gradient method와 매우 유사한 방식으로 작동한다. 그러나 Gradient method와 달리 Sub-gradient method는 다음과 같은 몇 가지 특징을 지닌다.

• Sub-gradient method는 non-differentiable한 f에 바로 적용될 수 있다.
• Step lengths를 line search를 통해 구하지 않는다. 대개 선제적으로 결정된 값이 사용된다.
• Sub-gradient method는 descent method가 아니다. 즉, 함숫값은 증가할 수 있고 때때로 그렇다.

이번 포스트에서는 이와 같은 차이점이 왜 발생하는지를 sub-gradient method의 원리를 중심으로 살펴볼 예정이다. 먼저 Sub-gradient가 무엇이며 이것이 수학적으로 어떤 성질과 의미를 지니는 지 학습하고, Sub-gradient method의 기본적인 작동 원리를 숙지할 것이다.

---

1. Definition

$domf$의 모든 $x$에 대해 모든 $z$가 다음을 만족할 때 vector $g$를 sub-gradient라고 한다. 따라서 어떤 점에서의 sub-gradient를 구하기 위해서는 다음과 같은 부등식을 풀어주면 되겠다.

그러나 이 정의는 다소 딱딱하기 때문에, 기하학적으로 sub-gradient를 이해함으로써 직관적으로 이 개념을 받아들여보겠다.

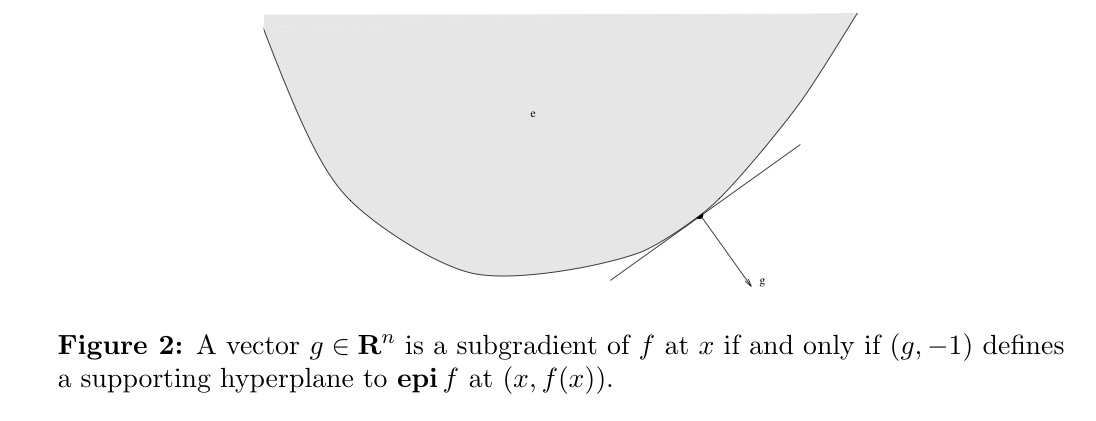
$f$가 convex function이고 $g$가 $f$의 특정 점 $\hat{x}$에서의 sub-gradient일 때, 정의에 의해 $f$의 모든 점 $x$에 대해 $f(x) \geq f(\hat{x}) + g^T(x-\hat{x})$을 만족한다. 이때 epigraph의 정의에 의해, $epi(f)$의 모든 점 $(x, t)$에 대해 $t\geq f(x)$이므로 부등식 $t\geq f(x) \geq f(\hat{x}) + g^T(x-\hat{x})$을 만족하여 $t\geq f(\hat{x}) + g^T(x-\hat{x})$ 의 관계가 성립한다. 이 식은 $g^Tx-t \leq g^T \hat{x} -f(\hat{x})$ 즉, $(g, -1)^T(x, t) \leq -f(\hat{x}) + g^T\hat{x}$ 라는 우변이 상수인 형태로 정리된다.

이것은 앞서 봤던 supporting hyperplane의 형태와 정확하게 일치하므로 $(g, -1)$을 $epi(f)$의 supporting hyperplane으로 이해할 수 있다.

sub-gradient의 존재성에 대해서는 세 가지 케이스로 분류하여 생각할 수 있다.

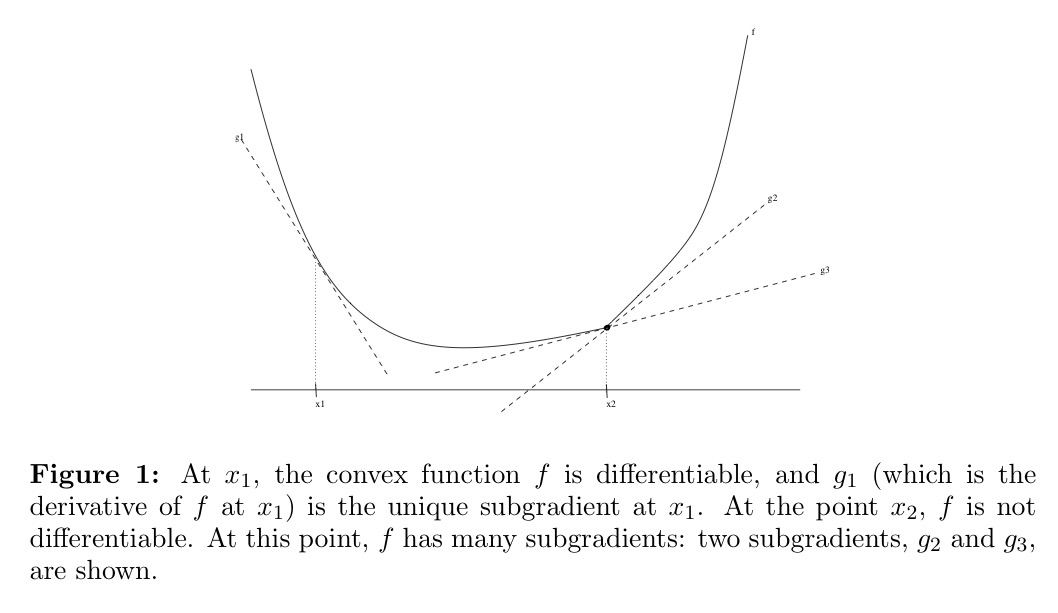
1. Convex한 function에 대해, $x_1$과 같은 미분 가능한 점에서는 sub-gradient가유일하게 존재
2. Convex한 function에 대해, 점 $x_2$와 같이 미분이 불가능한 점에서는 여러개의 sub-gradient가 존재할 수 있음
3. Non-convex한 function에서는 sub-gradient가 반드시 존재하지는 않음

정리하자면 sub-gradient는 미분이 불가능한 점에 대해서도 정의될 수 있다는 점에서 의의를 가지고, 함수의 convexity는 sub-gradient의 존재성을 보장해준다.

다음은 이번 포스트에서 자주 등장할 용어들이다.

• $f$의 어떤 점 $x$에 대해, 해당 점에서의 sub-gradient가 적어도 하나 존재할 경우 $f$는 $x$에서 sub-differentiable
• 해당 점에서의 모든 sub-gradient의 집합을 sub-differential of $f$ at $x$라고 하며 $\partial f(x)$로 표시
• 만약 $domf$의 모든 $x$에 대해 $f$가 sub-differential 하다면 $f$는 sub-differentiable

왼쪽에 있는 절댓값 함수 $f(z)=|z|$의 예시를 통해 sub-gradient의 컨셉을 이해해보자. 직접 식을 통해 계산하거나 $epi(f)$의 supporting hyperplane에 대해 생각하면 된다.

$x<0$과 $x>0$인 모든 부분의 sub-gradient는 각각 -1과 1로 해당 점들에서의 gradient와 정확하게 일치한다. 그러나 미분이 불가능한 점 $x = 0$에 대해서는, sub-gradient의 inequality가 $|z| \geq gz$로 정리되므로 $\partial f(0) = [-1, 1]$이라는 연속적인 구간이 sub-differential로 구해진다. 이것이 오른쪽 그림이다.

---

2. Basic Properties

Sub-gradient와 관련된 몇 가지 중요한 특성들을 받아들일 필요가 있다.

1. 만약 $f$가 $x$에서 미분가능하고 볼록함수라면, $\partial f$는 $\{\triangledown f(x) \}$만을 원소로 갖는다. 즉 sub-gradient가 유일하게 존재하고 그 값은 gradient와 같다.

2. 첫 번째의 역으로, 만약 $\partial f(x) = \{ g\}$이면 $f$는 $x$에서 미분 가능하며, $\triangledown f(x)$가 $g$가 된다. 즉 sub-gradient가 유일하게 존재하면 그 점에서 미분이 가능하고 gradient가 sub-gradient와 같은 값을 갖는다.

3. $\partial f(x)$는 $f$가 convex인지 아닌지와 무관하게 항상 closed convex set이 된다.

4. $f$가 $x$에서 연속이라면 sub-differential $\partial f(x)$는 항상 bounded 되어 있다.

5. $f$가 Convex하다면 $\partial f(x)$는 반드시 하나 이상의 원소를 가진다.
   (proof) $f$가 convex하다면 $epi(f)$ 역시 당연하게 convex하고, 따라서 $epi(f)$와 그 boundary에 있는 점, 즉 $(x, f(x))$에 대해서 Supporting hyperplane theorem을 적용할 수 있다.
   📌 Supporting hyperplane theorem
   Non-empty convex set인 C와 any $x_0 \in bd C$에 대해 $x_0$에서의 supporting hyperplane이 항상 존재한다. 즉 $a^T(x-x_0) \leq 0$을 만족하는 non-zero인 a가 존재한다.
   그렇다면 $epi(f)$의 점 $(z, t)$와 그 boundary point인 $f$$(x, f(x))$에 대해, 다음과 같은 식을 만족하는 non-zero $a$가 항상 존재한다.
   
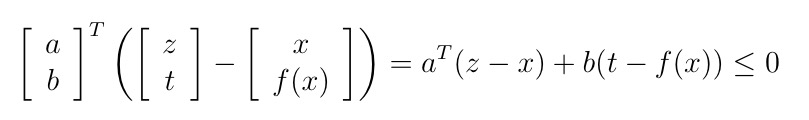
   여기서 어떤 $f(z)$ 값보다 $epi(f(z))$값인 $t$가 무조건 작거나 같으므로, 대신 $f(z)$를 대입해도 부등식은 성립한다.
   만약 b가 0이라면 $a^T(z-x) \leq 0$ 으로 식이 정리될텐데, 해당 부등식이 어떤 고정된 a 값을 갖고 있는 상태에서 모든 z에 대해 성립할 수 있음은 거짓임이 자명하므로 b는 0이 아니어야 한다.
   따라서 양변을 b로 식 정리를 할 수 있고, sub-gradient의 정의를 생각한다면 $-a/b \in \partial f(x)$, 즉 적어도 하나의 원소가 $\partial f(x)$안에 무조건 포함된다는 사실을 알 수 있다.

6. $x^*$가 함수 $f$의 minimizer가 되기 위한 필요 충분 조건은 g=0이 $x^*$에서의 $f$에 대한 sub-gradient 이다. 즉 0이 $\partial f(x^*)$ 안에 들어가 있다면 $x^*$는 $f$의 minimizer이고, 반대로 $x^*$가 $f$의 minimizer가 되기 위해서는 0이 $\partial f(x^*)$ 안에 들어가 있어야 한다.
   (⇒) $f(x) \geq f(x^*)$으로부터 너무 당연하게 $f(x) \geq f(x^*)+0^T(x-x^*)$가 유도된다.
   ($\Leftarrow$) $f(x) \geq f(x^*)+0^T(x-x^*)$는 $f(x) \geq f(x^*)$로 정리된다.
   *$f$가 convex이고 미분 가능하다는 조건이 추가되면 sub-gradient 값이 유일해지고 (따라서 0이 유일한 sub-gradient가 되고) sub-gradient 값과 gradient 값이 같아지는 (따라서 gradient가 0이 되는) 상황이 되므로 이 필요충분조건은 곧 ‘gradient가 0이다’라는 친숙한 문제로 탈바꿈된다.
   → 해당 성질은 다변수함수로 확장될 수 있다. 예컨데 다변수 함수 F(x, y)의 y에 대한 infimum이 x에서 구해질 때 $\partial F(x, y)$ 에는 (g, 0)이 들어 있어야 하며 이때의 g는 $\partial f(x)$이다

Set $\partial f(x)$를 구할 때에 있어서 주로 practical하게 사용되는 sub-gradient method들은 모든 sub-gradient를 요구하는 것이 아니라 하나의 sub-gradient 만을 요구한다. 따라서 이 Set에 들어있는 하나의 원소 g를 구하는 것으로도 충분하며, 이를 ‘weak calculus of sub-gradient’라고 칭한다. 다만 ‘strong calculus’를 통해 Set $\partial f(x)$의 모든 원소, 즉 set 그 자체를 밝혀내는 과정은 이론적인 측면에서 의미를 가질 수 있다.

---

3. Calculus of sub-gradients

Sub-gradient의 정의와 성질을 살펴봤으니 이제는 연산에 대해서도 이야기를 해봐야 한다. 다양한 연산과 관련되어 성립하는 주요한 규칙들을 간단히 살펴보도록 하겠다.

1. Non-negative Scaling
   $\alpha \geq 0$에 대해 $\partial(\alpha f)(x) = \alpha \partial f(x)$이 성립한다
2. Addition
   Convex function $f_1, ..., f_m$에 대해 $f=f_1+... + f_n$일때 $\partial f(x)=\partial f_1(x) +... + \partial f_m(x)$ 이다. 이는 infinite sum이나 integral 등으로 확장될 수 있다.
3. Affine transformation
   $f$가 convex일 때 $h(x)=f(Ax+b)$이면 $\partial g(x)=A^T \partial f(Ax+b)$이다.
4. Pointwise maximum
   $\partial f(x)$는 점 x에서 ‘active’한, 즉 점 x에서 f(x) 값을 갖는 함수들의 subdifferential의 합집합에 대한 Convex Hull이다.
   Why? Sub-differentiable한 Convex function $f_1, ..., f_m$에 대해 $f=max f_i(x)$로 정의될 때, $\partial f_i$들과 $\partial f$는 어떤 관계를 가질까?
   아래와 같은 함수들로 이루어진 pointwise maximum 함수가 있다고 하자. 그림 상에서 함수 $f$는 빨간색 선으로 표현될 것이다.
   
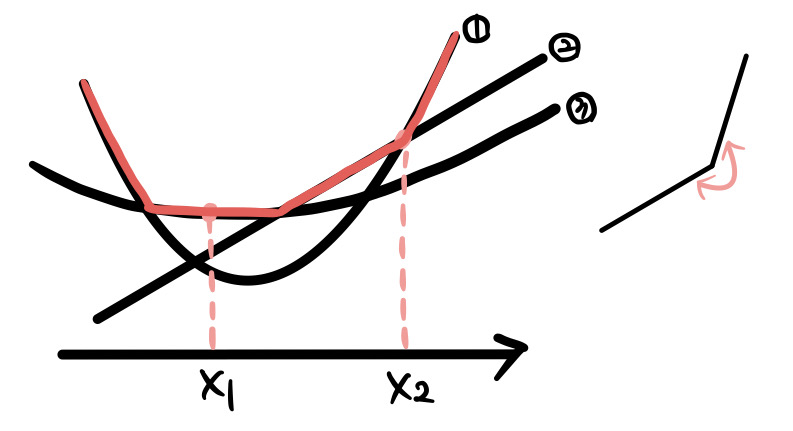
   이때 어떤 한 점, 예를 들어서 $x_1$을 잡았을 때, $x_1$에서의 pointwise maximum을 제공해주는 함수는 3번 함수이다. 이때 이 점에서의 sub-gradient를 생각해보면, 그냥 3번 함수의 $x_1$에서의 sub-gradient가 될 것이다. 해당 점의 최댓값은 3번 함수를 통해서만 얻어질 수 있기 때문이다.
   그러나 $x_2$는 다르다. 이 점은 f의 입장에서 일종의 첨점, 즉 미분이 불가능하여 sub-gradient가 여러 개 존재할 수 있는 점이다. 해당 점의 최댓값은 둘 이상의 함수, 즉 여기서는 1번 함수와 2번 함수를 통해 얻어질 수 있다.
   그렇다면 1번 함수와 2번 함수 각각의 sub-gradient를 $\partial f(x_2)$에 넣어보자. 그림을 그려서 생각해보면 당연히 둘 다 $\partial f(x_2)$에 있다. 즉, $\partial f_1(x_2)$와 $\partial f_2(x_2)$는 모두 $\partial f(x_2)$의 subset이 된다.
   
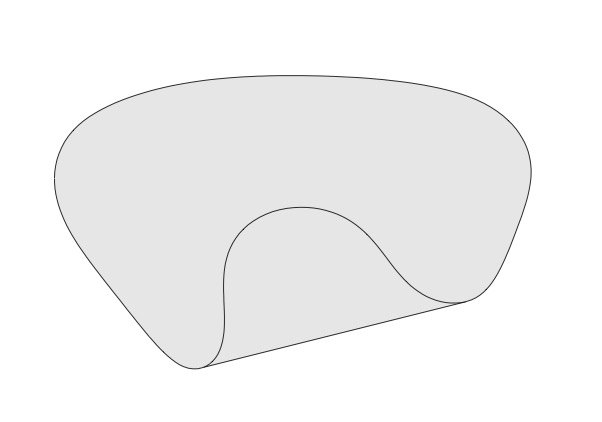
   그렇다면 $\partial f(x_2)$에는 이들만 있을까? 그렇지 않다. 그림에서 이 두 직선 사이에 그려지는 모든 직선들이 의미하는 $g$값이 $\partial f(x_2)$안에 들어가야 한다. 이는 Convex hull의 컨셉과 유사해보이며, 수학적으로도 그렇다.
   $\partial f(x) = Conv(\cup_{i: f_i(x)=f(x)} \partial f_i(x))$
   정리하자면, $\partial f(x_2)$의 모든 원소들은 $\partial f_1(x_2)$와 $\partial f_2(x_2)$ 합집합이 형성하는 Convex Hull의 원소들과 정확하게 일치한다. 따라서 이를 위와 같은 수식으로 일반화 할 수 있다.

---

4. Quasi-gradients

점 $x_0$ 에서의 quasi-gradient는 g는 f가 quasi-convex일 때 다음과 같은 상황에서 정의된다.

Sub-gradient가 $f(x) \geq f(x_0)+g^T(x-x_0)$로 정의됨을 떠올렸을 때 quasi-gradient는 sub-gradient가 어느정도 완화된(?) 형태라고 간주할 수 있겠다.

---

5. Basic Sub-gradient Method

Sub-gradient가 무엇인지에 대한 탐색은 어느정도 마무리된 것 같으니 Sub-gradient method로 넘어가도록 하겠다. 먼저 제약조건이 없는 Convex한 함수를 minimize하는 가장 기본적인 경우에 대해 논해보도록 하겠다. 이를 위해 sub-gradient method는 다음의 간단한 iteration을 사용한다.

$x^{(k)}$: k번째 iterate
$g^{(k)}$: f의 $x^{(k)}$에서의 아무 sub-gradient
$\alpha_k >0$: k번째 step size

*$g$에 대해서는 set notation을 이용하여 $g^{(k)} \in \partial f(x^{(k)})$로 표현할 수 있다. 따라서 만약 해당 점에서 f가 미분 가능하다면, $g^{(k)}$의 선택지는 $\nabla f(x^{(k)})$밖에 없어지므로 step size의 선택 방식을 제외하고는 gradient method와 동일해진다.

Gradient method의 iteration 수식은 $x^{(k+1)} = x^{(k)}+\alpha_k \nabla f(x_i)$로, 이는 gradient 값이 극솟값에 가까울수록 작아진다는 원리를 이용하여 이동거리를 gradient의 크기와 비례하게 설정한 결과물이다. 이를 통해 현재의 $x$값이 극솟값에서 멀 때는 많이 이동하고, 가까울 때는 조금씩 이동할 수 있게 된다.

그러나 이 식에 gradient 대신 sub-gradient를 대입할 경우, k+1번째 iterate의 함수값이 k번째 iterate의 함수값보다 극솟값에 가깝다고 보장해주지 못한다. 즉 object function이 증가하게 될 수도 있다.

(Proof) Sub-gradient method를 sub-gradient ‘descent’ method가 아니다.

$g^k$는 $x^k$에서의 sub-gradient 이므로, sub-gradient의 정의에서 z 자리에 $x^{(k+1)}$을, x 자리에 $x^{(k)}$를 대입하면 식은 다음과 같이 정리된다.

정리하자면 $f(x^{(k+1)})$은 $f(x^{(k)})-\alpha||g^k||^2_2$ 보다 크거나 같은 값을 갖게 되는데, $-\alpha||g^k||^2_2$은 0보다 크거나 같아도 되며 상한이 주어져 있지 않으므로 $f(x^{(k+1)})$은 때때로 $f(x^{(k)})$보다 크거나 같은 어떤 값을 가질 수 있다.

따라서 매 스텝마다 현재의 $f$값과 바로 이전의 $f$값 중 무엇이 더 작은지를 판별해주어야 하고, $k$번의 iteration을 마친 뒤에는 $k$개의 $f$값들을 전부 기억해두었다가 무엇이 가장 작은지를 재차 판별해주어야 한다. 즉, 우리가 찾고자 하는 점에서의 $f$값은 다음과 같은 노테이션을 통해 표현된다.

이와 같은 이유로 Sub-gradient method는 Newton’s method, interior-point method 등의 second-order methods들 보다 매우 느리다*. 그러나 범용성의 측면에서 이점을 갖기 때문에 사용되는 것이다.

그렇다면 step size는 어떻게 정해지는 것일까? Sub-gradient method에 사용되는 step size는 gradient descent에서와는 다르게 미리 설정되어야 한다. 가장 기본적인 몇 가지 예시는 아래와 같다. 전부 옆의 제약을 만족하는 알파를 자율적으로 step size로서 설정하면 된다.

• Constant step size. $\alpha_k = \alpha$는 $k$와 독립인 양의 상수
• Constant step length. $\alpha_k =\gamma/||g^{(k)}||_2, \ where\ \ \gamma>0.$ $||x^{(k+1)}-x^{(k)}||_2=\gamma$
• Square summable but not summable. $\alpha_k \geq0, \ \Sigma_{k=1}^\infin \alpha_k^2 < \infin, \ \Sigma_{k=1}^\infin \alpha_k =\infin$
• Nonsummable diminishing. $\alpha_k \geq0, \ \lim_{k\rightarrow \infin} \alpha_k =0, \ \Sigma_{k=1}^\infin \alpha_k =\infin$
• Nonsummable diminishing step lengths. $\alpha_k =\gamma/||g^{(k)}||_2, \ where\ \ \gamma_k>0,\ \lim_{k\rightarrow \infin} \gamma_k =0, \ \Sigma_{k=1}^\infin \gamma_k =\infin$

기억해야 할 점은 Sub-gradient의 step size는 알고리즘이 돌아가기 전에 결정되어 있으며, 알고리즘이 돌아가는 동안 도출되는 그 어떤 데이터와도 무관하다는 사실이다.

---

6. Convergence Proof

먼저 세 가지 가정을 하도록 하겠다.

1. f에 대한 minimizer인 $x^*$가 존재한다.
2. Sub-gradient들의 norm에는 유계가 있다. (모든 k에 대해 $||g^{(k)}||_2 \leq G$인 G가 존재)
3. Initial point와 optimal set 사이의 거리에 대한 상계가 알려져 있다. ($R \geq ||x^{(1)}-x^*||$)

앞으로 Step size가 어떻게 정의되는 지에 따라 수렴성이 어떻게 달라지는 지 자세하게 살펴볼 것이다. 그 전에 다음과 같은 basic inequality를 정의하도록 하고 이와 같은 부등식이 도출되는 과정을 잠시 보고 돌아오도록 하겠다.

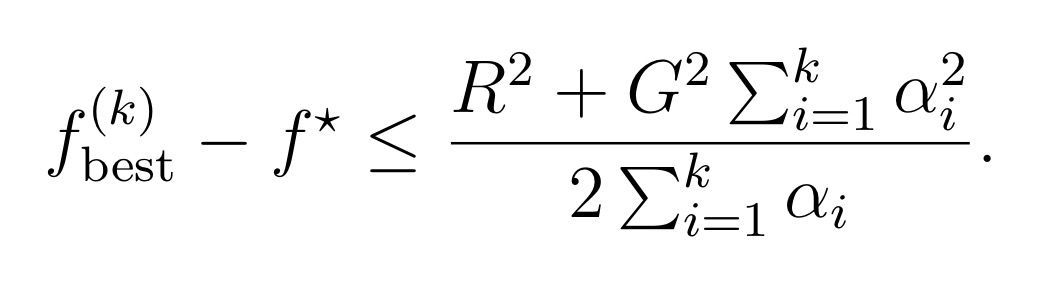
Step 1 : ‘$k$+1번째 point와 optimal set’ 사이의 distance의 제곱과, ‘$k$번째 point와 optimal set’ 사이의 distance의 제곱 사이 관계에 대해 식 a와 같은 부등식을 생각해볼 수 있다.

• 등호 부분은 자명함 (iteration 식 정의를 이용, 제곱 텀을 전개)
• 부등호의 경우 g가 sub-gradient이므로 정의를 이용해서 도출 가능

Step 2 : 다음으로, 식 a의 $k$자리에 1부터 n까지의 숫자를 대입한 식을 펼쳐주고 모든 식의 양변을 더해주겠다. 그러면 값들이 소거되어 식 b와 같이 정리된다.

Step 3 : Norm의 제곱이 무조건 0보다 크거나 같아야 한다는 사실과 세 개의 가정 중 마지막 가정을 사용해서 부등식을 확장시켜주겠다. 결과적으로 식 c가 도출된다.

Step 4 : 하나의 부등식을 추가적으로 생각해주겠다. 당연히 $\alpha_i$i와 각각의 $f(x_i)-f^*$를 곱한 값들의 합보다는, 이들 중 가장 작은 값을 일괄적으로 모든 $\alpha_i$에 곱해 더한 합이 더 작을 것이다. 이때 optimal value와의 차이가 최소화되기 위해서는 $f(x_i)$가 $*k$번 iteration 하는 동안 등장한 모든 함숫값들 중에서 가장 ‘좋은 점’, 즉 극솟값에 가장 가까운 점으로 설정*되어야 한다. 이를 이용해 증명을 전개해나가면 식 d를 얻을 수 있다.

Step 5 : 마지막으로, 2번 가정을 사용하여 general inequality를 도출한다. 이 general inequality는 step size의 정의에 따라 수렴성이 어떻게, 또 왜 보장되는지를 논할 때 사용된다.

예를 들어 Constant step size의 경우, Basic inequality의 우변이 $(R^2+G^2\alpha^2k)/2\alpha k$로 정리되므로 $k$가 무한대로 갈 때 $G^2 \alpha/2$로 수렴한다. 즉 optimal value와 최대 $G^2 \alpha/2$ 내로 차이나는 값에 반드시 도달한다. 나아가 이러한 sub-optimal에 $R^2/(G^2 \alpha^2)$ step 내로 도달하게 됨을 보일 수 있다.

Basic step size rules 각각에 대한 결과는 다음과 같다.

• Constant step size. $\alpha_k = \alpha$, where $\alpha$ is positive constant independent with $k$
• Constant step length. $\alpha_k =\gamma/||g^{(k)}||_2, \ \mathsf{where}\ \ \gamma>0.$ $||x^{(k+1)}-x^{(k)}||_2=\gamma$
• Square summable but not summable. $\alpha_k \geq0, \ \Sigma_{k=1}^\infin \alpha_k^2 < \infin, \ \Sigma_{k=1}^\infin \alpha_k =\infin$
• Nonsummable diminishing. $\alpha_k \geq0, \ \lim_{k\rightarrow \infin} \alpha_k =0, \ \Sigma_{k=1}^\infin \alpha_k =\infin$ → converges.
• Nonsummable diminishing step lengths. $\alpha_k =\gamma/||g^{(k)}||_2, \ where\ \ \gamma_k>0,\ \lim_{k\rightarrow \infin} \gamma_k =0, \ \Sigma_{k=1}^\infin \gamma_k =\infin$ → converges.

따라서, 모든 경우에 대해 수렴성이 보장됨을 확인할 수 있다.