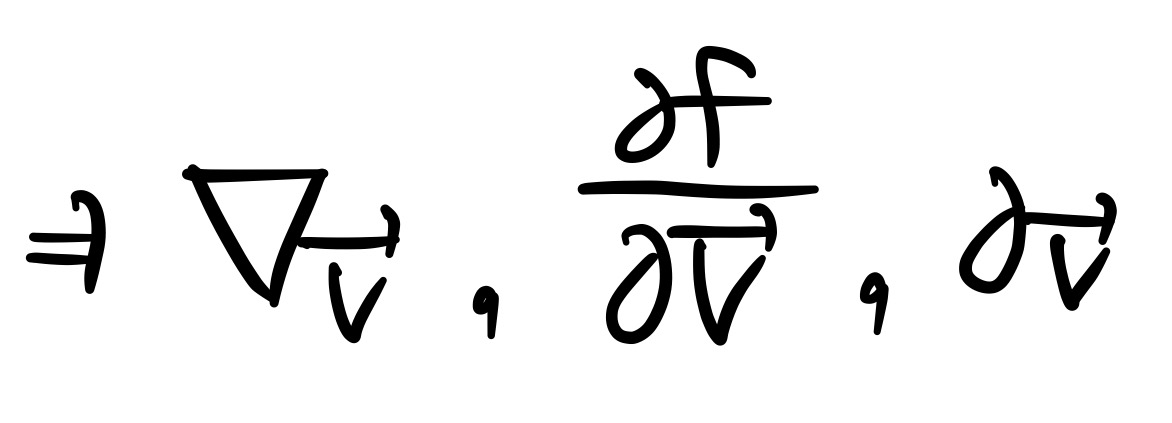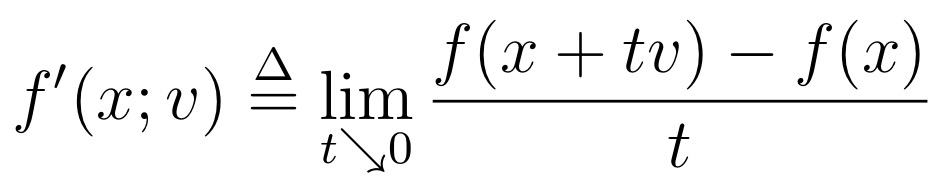[Week 3] Sub-gradient Method [2]

1. Polyak’s Step Length

이번 포스트에서는 먼저 Polyak이 제안한 step length 선택 방법에 대해 알아볼 예정이다. Optimal value인 $f^\star$를 알 때, 아래와 같은 step size를 선택할 수 있다.

어떻게 이러한 step size가 도출되는 것일까? 아래의 식을 보자.

좌변을 $f^*$로 대체하고 $\alpha$에 대해 정리하면 위와 같은 step length가 얻어지는 것을 확인할 수 있다. 나아가 지난 포스트에서 확인했던 식 $2 \sum ^k _{i=1} \alpha_i (f(x_i)-f^*) \leq R^2 + \sum ^k _{i=1} \alpha ^2_i ||g^{(i)}||^2_2$ 의 step size 자리에 $\alpha_k$를 대입하고 정리함으로써 Convergence를 확인할 수 있다.

또한 suboptimality인 $\epsilon$ 을 보장하는 steps의 수는 $k=(RG/\epsilon)^2$ 이다.

---

2. Polyak step size choice with estimated $f^*$

위의 step size $\alpha_k$는 $f^*$를 알아야 계산될 수 있는데, 이번에는 이 optimal value를 $f_{\text{best}}-\gamma^k$로 estimate 하는 방법에 대해 다루고자 한다. 이때 $\gamma^k$는 $\gamma^k \gt 0,$ $\gamma^k\rightarrow 0$를 만족한다.

step size : $\alpha_k=\dfrac{f(x^{(k)})-f^{(k)}_{\text{best}}+\gamma_k}{||g^{(k)}||^2_2},$ $(\sum^{\infin}_{k=1}\gamma_k=\infin)$

이때의 $\gamma_k$ 는 현재 point의 estimate of suboptimal 이며, $\sum^{\infin}_{k=1}\gamma_k=\infin$을 만족한다. 그렇다면 $f_{\text{best}}^{(k)} \rightarrow f^\star$ 이 만족된다. 이번에도 수렴성을 살펴보자.

만약 $f^{(k)}_{\mathsf{best}}-f^* \geq \epsilon > 0$ 라면 $i=1, ..., k$에 대해 $f(x^{(i)})-f^* \geq \epsilon$가 만족되고, 이는 곧 $(f(x^{(i)})-f^*)+(f^{(i)}_{\text{best}}-f^*)-\gamma_i \geq \epsilon$을 암시한다. 이때 위의 합을 쪼갬으로써 아래와 같은 관계식을 도출할 수 있다.

이제 $f(x^{(i)})-f^{(i)}_\mathsf{best}+ \gamma_i \geq \gamma_i$와 $||g^{(i)}||^2_2 \leq G$를 이용하여 수렴성을 최종적으로 확인하자.

이때 좌변이 $\infin$ 으로 converge하고 우변이 변수 $k$에 대한 식이 아니므로 $k$는 너무 클 수 없다.

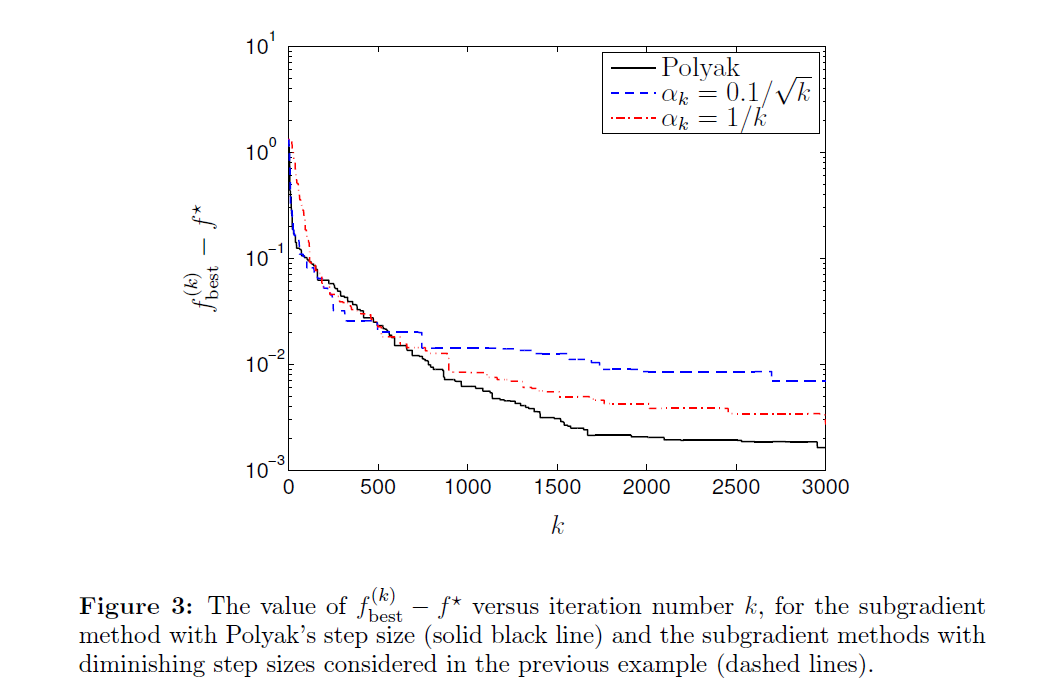
Piecewise linear example을 Polyak’s step size로 진행한 sub-gradient method의 결과이다. 문제를 풀기 전에는 $f^\star$ 의 값을 모르기 때문에 사실 현실적인 문제들에 적용하기는 어렵다. 또한 수렴 속도가 꽤 느린 것을 관찰할 수 있다.

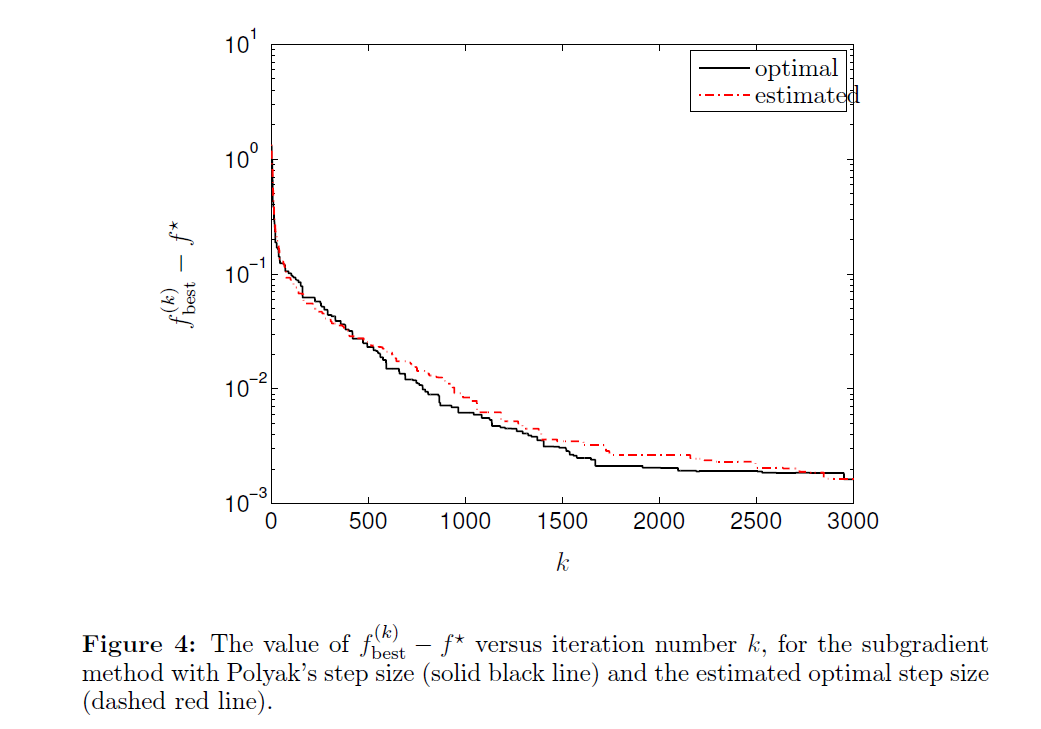
똑같은 문제의 optimal step size와 estimated step size에 대한 $f^k_{\text{best}}$ 를 보여준다. Estimated optimal value를 사용한 Polyak step size가 known optimal value의 step size만큼 좋은 결과를 보이고 있다.

---

3. Alternating Projection

Alternating projections method는 convex sets들의 intersection에 있는 점을 찾는 기법으로, 이 과정에서 Polyak’s step이 어떻게 사용되는지를 설명하고자 한다.

$C_1,...,C_m \sube \bold R^n$ 이 closed and convex한 sets일 때, $C=C_1\cap \cdots \cap C_m$ 에 있는 점을 찾는 문제는 다음 함수를 minimizing함으로써 풀 수 있다.

이때 $f(x)$는 convex하고 $f^\star=0$ 이라는 minimum value를 갖는다. 그리고 $f$의 $x$에서의 sub-gradient $g$를 찾는 방법은 다음과 같다. $(f(x)=0$ 이면 $g=0$ 이다$)$

$g=\nabla\bold{dist}(x,C_j)=\dfrac{x-\prod_{C_j}(x)}{||x-\prod_{C_j}(x)||_2}$

이때 $\prod_{C_j}$ 는 $C_j$로의 Euclidean projection이고 $||g||_2=1$ 이므로 $G=1$ 이다. $j$를 $x^{(k)}$가 $C_j$에 최대 거리를 가지는 index라 정의하고, 앞에서 나온 step size 식을 활용하여 sub-gradient algorithm을 update하면 다음과 같은 결과를 얻는다.

이때 두 번째 줄에서 $||g^{(k)}||_2=1$ 과 $f^\star=0$ 을 사용하면 다음과 같은 식을 얻는다.

이는 현재의 점을 가장 먼 set에 projection 시키는 간단한 알고리즘이다. Alternating projections algorithm의 확장판이라고 생각하면 된다. 유의해야 할 것은, $f(x^{(k)}) \rightarrow f^\star=0$ 은 보장되지만 $C$ 안에 있는 정확한 점을 찾는 것은 보장되지 않는다는 점이다. 교재에서는 이를 해결하기 위한 크게 두 가지의 방법을 제시하고 있다.

(1) Closed sets인 $\tilde{C_i}\sube \bold{int}C_i$ 를 사용하여, $x^{(k)}\rightarrow \tilde{C}=\tilde{C_1}\cap \cdots \cap \tilde{C_m}$ 이 만족된다면 $x^{(k)}\in C$ 인 $k$가 존재함을 이용한다.

(2) 각 step에 over-projection을 한다. 즉 $C$에 radius $\epsilon$인 Euclidean ball을 있다고 가정하면 Euclidean ball의 center인 현재의 점을 가장 먼 set에 project 하면서 $\epsilon$ 을 바꿀 수 있다.

$x^{(k+1)}=\prod_{C_j}(x^{(k)})-\epsilon \dfrac{x^{(k)}-\prod_{C_j}(x^{(k)})}{||x^{(k)}-\prod_{C_j}(x^{(k)})||_2}$

이런 alternating projections은 projection하는 sets이 간단할 때 주로 사용한다.

이번에는 Convex inequalities를 다루는 방법에 대해 살펴보자. $f_i(x) \le 0,~ i=1,…,m$ 을 만족하는 점을 찾는 문제가 있다. 이런 convex inequalities의 set을 풀기 위해서는 subgradient method를 사용하여 unconstrained function인 $f(x)=\max_i f_i(x)$ 를 minimize해야 한다. 이때 inequalities가 strictly feasible하면 $f^\star \lt 0$이고, finite한 step을 통해 $f(x) \le 0$ 인 점을 찾을 수 있다.

$\epsilon \gt 0$ 이 tolerance일 때 $f(x)=\max\{ f_1(x),…,f_m(x),-\epsilon\}$ 에 대하여 $f_i(x)\le -\epsilon$ 인 점이 있다고 가정하면 step length 는 다음과 같다.

step size : $\alpha=\dfrac{f(x)+\epsilon}{||g||_2^2}$

간단함을 위해 $\epsilon = 0$ 이라 가정하고 위의 step length에 대한 해석을 해보자. 현재의 점 $x$ 에 대하여 $f_i(x)=f(x) \gt 0$ 이고 $g \in \partial f_i(x)$ 라 하자. $x^\star$가 $f_i(x^\star) \le 0$인 점이라면 다음을 얻는다.

즉, $\mathcal{H}=\{z ~|~0 \ge f_i(x)+g^T(z-x) \}$에 대해 $x \in \mathcal{H}$이다. 우리는 Polyak’s step length를 사용하여 $x$에서의 sub-gradient를 업데이트하는 것이 $x$를 $\mathcal{H}$에 projection하는 것과 같음을 알 수 있다.

마지막으로, sub-gradient method가 positive semidefinite matrix completion problem을 푸는 데 어떻게 사용될 수 있는지를 살펴보자. 이는 $\bold S^n$에 있는 matrix에 대해 diagonal entries을 포함한 몇몇의 entries 이 고정되어 있는 상황에서 다른 entries 들을 채워넣어야 하는 문제이다. 목표는 빈 entries들을 채워넣어 matrix가 positive semidefinite가 되도록 만드는 것이다.

Positive semidefinite matrices 인 $\bold S^n_+$의 set 과 고정된 entries 로 이루어진 matrix에서 alternating projection 을 사용한다. 첫 번째 projection은 eigenvalue decomposition 을 통해 찾을 수 있다. $X=\sum ^n_{i=1}\lambda_i q_i q_i^T$ 라 하면 $\prod(X)=\sum\limits^n_{i=1}\max \{0,\lambda_i\}q_i q_i^T$이다. 두 번째 projection은 주어진 matrix의 fixed entries들을 fixed values 로 바꾸면 된다.

$50\times 50$ matrix의 예시를 보면 unknown entries 들이 positive semidefinite completion 으로 아주 잘 수렴하고 있음을 관찰할 수 있다.

---

4. Projected sub-gradient method

이번에 살펴볼 Projected sub-gradient method는 sub-gradient method의 확장으로, convex set으로의 제약 조건이 있을 때 optimization 문제를 풀기 위한 방법이다.

Projected sub-gradient method는 다음과 같이 주어진다.

그냥 sub-gradient method와 비교했을 때 $\Pi$가 추가된 점이 다르다. 이 $\Pi$는 constraint set $\mathcal{C}$로 projection 해주는 operator, 즉 negative sub-gradient 방향으로 이동한 뒤 projection 해준다는 의미를 지닌다 이때의 convergence는 standard case와 동일하게 성립한다.

$z^{(k+1)}$을 projection 전의 point로 놓고 optimal point와의 distance에 대입해 정리해 보자.

이때 $z^{(k+1)}$을 $\mathcal{C}$로 projection 시켰으므로 $\mathcal{C}$ 안의 점인 optimal point에 더 가까워지는 것은 당연하다. 따라서 $\lVert x^{(k+1)}-x^* \lVert_2^{2}\,\leq \lVert z^{(k+1)}-x^* \lVert_2^{2}$ 이고, 이 둘을 합치면 $\lVert x^{(k+1)}-x^* \lVert_2^{2}\, \leq\lVert x^{(k)}-x^* \lVert_2^{2}\,-2\alpha_k(f(x^{(k)})-f^*)+\alpha_k^2 \lVert g^{(k)} \rVert_2^2$ 의 inequality를 얻을 수 있다. 이는 standard sub-gradient method의 convergence 증명에서 얻은 결과와 일치하므로, projection이 convergence에 영향을 미치지 않는다는 것을 알 수 있다. 앞에서 나온 Polyak’s step length를 적용해도 convergence는 동일하게 성립한다고 한다.

만약 $\mathcal{C} =\left\{x\,|\,Ax=b\right\}$꼴의 affine set이라면 $Ax^{(k)}=b$이므로 $A$의 null space로 projection해주면 된다. 그리고 null space는 $A^T$의 column space의 orthogonal complement이므로 sub-gradient update는 아래와 같이 도출된다.

이처럼 operator를 연산하기 쉬운 경우에는 projected sub-gradient method를 잘 사용할 수 있다.

(Example) l1 norm problem

${\displaystyle {\begin{aligned}&{\text{minimize }}\lVert x \rVert_1\\[0.5ex]&{\text{subject to }}Ax=b\end{aligned}}}$

$x\in \mathbb{R}^n$이고 A는 full column rank라고 가정하자. l1 norm의 subgradient는 sign(x)이다. 따라서 업데이트 공식은 아래와 같다.

$x^{(k+1)}=x^{(k)}-\alpha_k(I-A^T(AA^T)^{-1}A)\mathbf{sign}(x^{(k)})$

이번에는 dual problem에 대해 projected sub-gradient를 적용해보자. convex optimization problem의 dual problem을 정의하는 것은 익숙하다.

strong duality가 성립할 때, (가령 slater’s condition을 만족할 때) lambda의 optimal값을 구한 뒤 역으로 x의 optimal 값을 구할 수 있었다. ($x^*=x^*(\lambda^*)$ 이 dual problem 역시 sub-gradient method를 이용해 풀 수 있다. 업데이트 식은 다음과 같다.

라그랑지안에 대한 sub-gradient는 아래와 같이 찾을 수 있다.

Dual problem에 대한 projected sub-gradient method의 업데이트 식은 다음과 같이 정의된다.

이때 primal variable x는 limit에서만 feasible하다. 또한 dual function value와 primal function value는 optimal로 같이 수렴한다.

---

5. Sub-gradient method for constrained problem

제약 조건이 있는 convex optimization의 경우에도 sub-gradient update 식은 앞과 똑같다. 다만 현재 x값이 feasible, infeasible한지에 따라 objective의 sub-gradient를 사용할지, 또는 violated된 constraint의 아무 subgradient를 사용할지가 달라진다.

다 결국 iteration이 반복됨에 따라 optimal point로 수렴함을 귀류법으로 증명할 수 있다. Polyak’s step length를 사용하고 $f^*$를 안다고 하면 현재 상태가 feasible이냐, infeasible이냐에 따라 아래와 같이 step size를 선택한다.

---

A. Directional Derivative

Directional Derivative의 개념이 포스트 전반에 등장하여, 이를 쉽게 이해할 수 있도록 Kahn Academy의 아래 영상 내용과 기타 자료들을 정리하였다.

https://www.youtube.com/watch?v=N_ZRcLheNv0

Directional derivative, ‘방향도함수’라고 칭해지는 이 개념은 쉽게 말해 편도함수의 확장이라고 볼 수 있다. $f(x, y)=x^2 y$로 정의된 함수를 생각해보자. 해당 함수는 두 개의 변수 즉 multivariable을 받아서 하나의 실수를 출력하는 함수이다. 따라서 input space와 output space를 다음과 같이 표현할 수 있다.

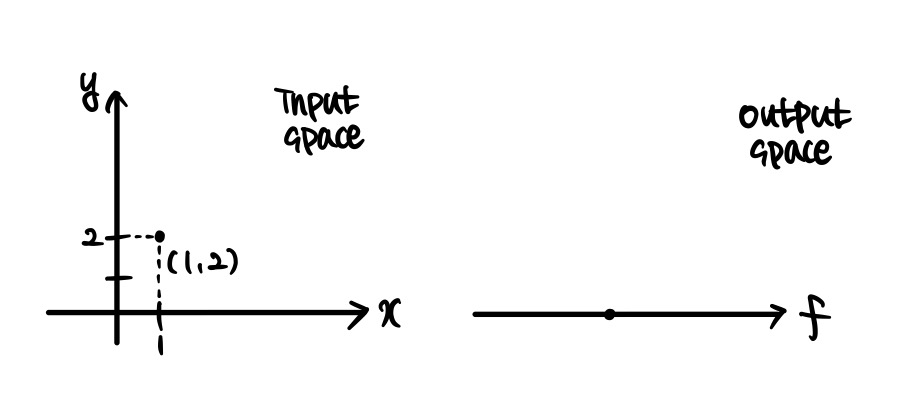
이때 우리가 아는 편도함수와 편미분의 개념에 대해 생각해보자. $\partial f/ \partial x (1, 2)$가 의미하는 것은 무엇인가? 바로 input space의 점인 (1, 2)를 x축 방향으로 아주 조금 이동했을 때 출력값이 얼마나 이동해야 하는지를 의미한다. 이 출력값이 이동한 거리와 입력값이 이동한 거리의 비가 f의 x에 대한 편도함수에 입력값을 대입한 결과값이 되는 것이다. $\partial f/ \partial y (1, 2)$도 마찬가지로 해석될 수 있다. 참고로 지금 그림들은 과장해서 그린 것이며, 실제로는 가시적인 변화가 아닌 아주 작은(0에 수렴하는) 변화에 대해 생각하고 있다.

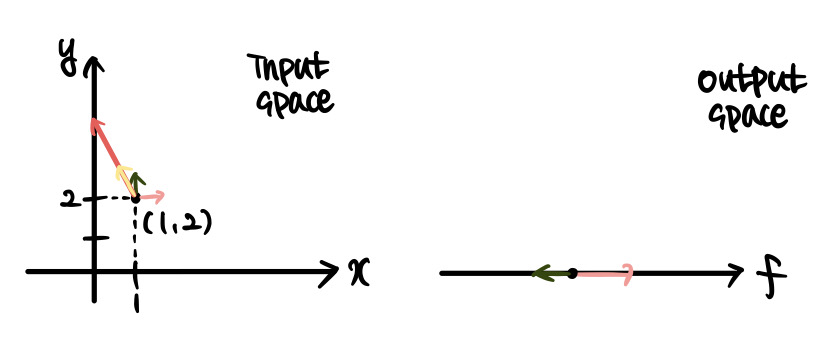
그렇다면 방향 도함수란 무엇인가? (1, 2)를 시점으로 하는 벡터 $v$를 $[-1, 2]^T$로 정의하도록 하겠다. 방향 도함수의 관심사는 이것이다. 입력값을 x나 y 방향이 아닌, 이 벡터의 방향으로 움직인다면 출력값에는 어떤 영향이 갈 것인가? 이 입력값의 변화를 식으로 표현하면 $tv$가 될 것이다(여기서 t는 아주 작은 값이다). 그리고 우리가 정의한 $v$값에 따라 $[-h, 2h]$로 표현할 수 있다. 이는 수학적으로 다음과 같은 노테이션을 이용해 표현된다.

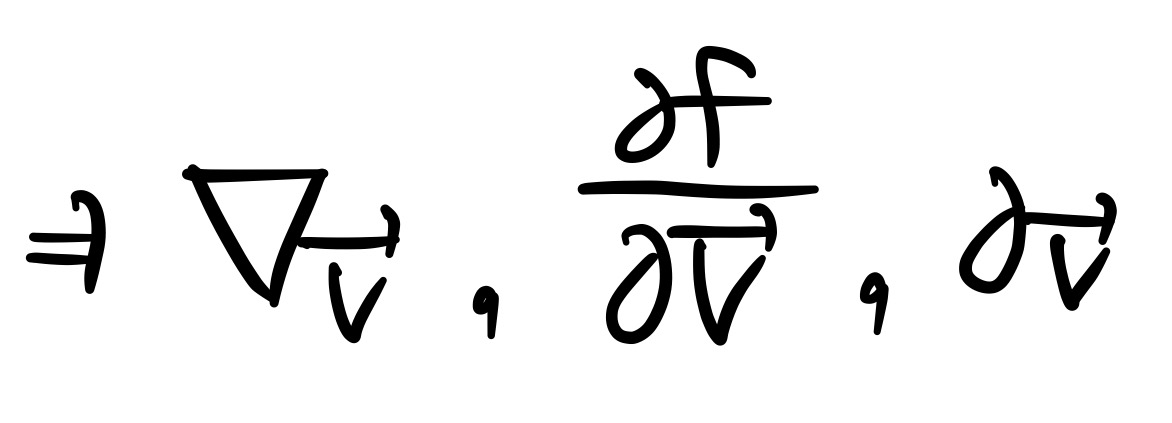
$[-h, 2h]$를 보면 방향도함수가 어떤 식으로 계산될 지를 어느정도 예상해볼 수 있다. 아주 작은 단위 h만큼을 x축 방향으로 -1칸, y축 방향으로 2칸 움직였으니 $-(\partial f/\partial x)+2(\partial f/\partial y)$ 임을 예상할 수 있고, 실제로도 그렇다. 이를 gradient form으로 일반화 해보자면, 벡터 $w$가 $[a, b]^T$로 정의될 때 $\triangledown_wf=w \cdot \triangledown f = w^T\triangledown f$로 나타낼 수 있다.

그리고 f가 점 x에서 미분 가능하다는 것의 필요충분조건은 방향도함수 값이 어떤 g에 대해서 $f^\prime(x;v)=g^Tv$ (여기서 g는 $\triangledown f(x)$이다) 의 linear한 형태로 표현되는 것이다. 위에 적은 노테이션을 참고했을 때 좌변이 우변의 형태로 정의되기 위해서는 일단 $\triangledown f$가 정의되어야 하기 때문이라고 생각하면 될 것 같다.

이제 교재의 내용으로 돌아와서, Convex function $f$에 대해 점 $x$에서의 $v$ 방향으로의 방향도함수는 수식적으로 다음과 같이 정의된다.

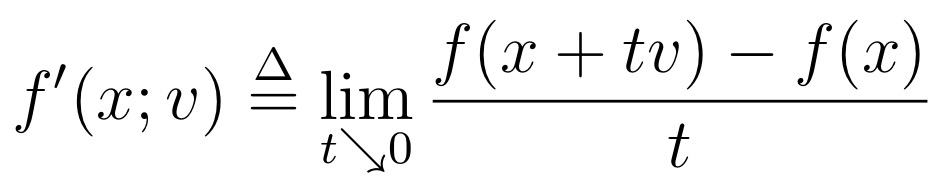
이 방향도함수는 몇 가지 성질을 지니는데, 교재에 나온 성질 중에서 함수의 convexity와 관련된 부분만 얘기하고 넘어가도록 하겠다. $**f$가 v에서 convex하고 $x$의 주변에서 finite 하다면 $f^\prime(x;v)$는 존재한다**. 좀 더 러프하게 말하자면, (비록 $\pm \infin$의 값을 가질 수는 있지만) convex function f의 모든 점은 방향도함수 값을 가진다.

그림으로 살펴보자면, 다음과 같이 convex한 function에 미분 불가능한 점이 있다고 해도 이 점은 이 근처에서는 미분이 가능하기에 방향도함수를 갖는다. 예를 들어 아래의 점을 기준으로 1과 -1이 다른 방향에 있는 상황일 때, $f'(x; 1)$은 $f'_+(x)$이고 $f'(x; -1)$은 $f'_-(x)$이 된다. 미분 가능하다는 것은 곧 이 방향도함수 값들이 서로 같은 값을 갖는 상황인 것이다.

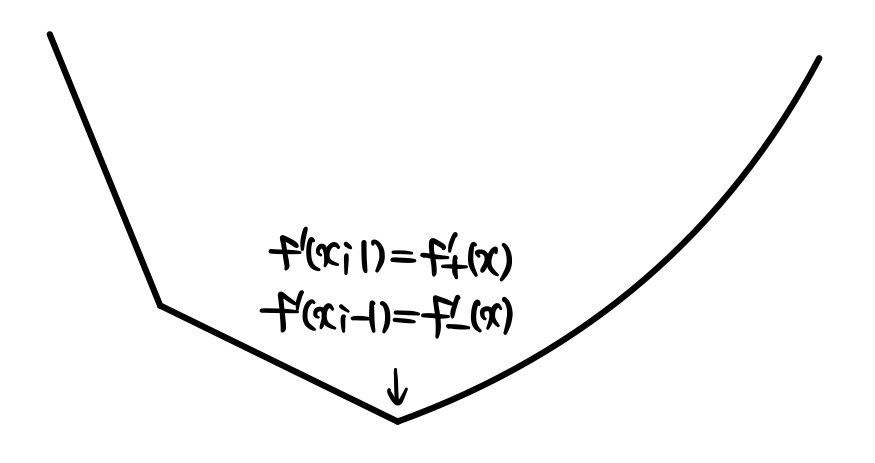
그리고 방향도함수는 convex function $f$에 대해 다음의 관계를 만족한다.

이 등식을 증명하는데 sub-gradient의 개념이 이용된다. $f$가 $x$에서 미분가능하다면 그 gradient 값이 곧 sub-gradient 값과 동일하다. 따라서 sub-gradient의 정의에서 $z$자리에 $x+tv$를 넣어보겠다. 이때 식은 다음과 같이 정리되는데: $f(x+tv)-f(x) \geq tg^Tv$, 여기에 리미트를 붙인게 방향도함수이고 모든 t와 g값에 대해서 이 식이 성립해야 하므로 (즉, 우변의 sup에 대해서도) $f^\prime (x;v) \geq sup_{g \in \partial f(x)} \ g^Tv$가 만족된다.

이때 f가 x에서 미분 가능하다면 f가 어떤 g에 대해 $f^\prime(x;v)=g^Tv$ 꼴로 표현된다고 했기 때문에 등호가 성립한다고 생각할 수 있다.