[Week 4] Robust Optimization [1]

* 세션 교재: Stanford university - EE364b - Convex Optimization II lecture note - John Duchi.

Introduction

우리가 얻을 수 있는 데이터 중 '완전한 것'은 거의 없다. 가령 모델을 돌리면 잘 훈련되는 듯 하지만, 테스트 결과는 영 쓸모가 없는 경우를 많이 겪어보았을 것이다. 만일 실제 산업에서 이런 일이 발생한다면 어마어마한 손해가 생길 수 있다.
이런 일이 발생하는 이유는 데이터의 불완전성 때문이다. 가령 A금융사에서 고객 데이터를 가졌다고 하자. A금융사는 이것을 이용해 고객을 더 끌어올 목적으로 새로운 서비스를 개발했다. 그러나, 생각보다 고객은 잘 늘어나지 않을 수 있다. 왜냐하면 A금융사가 가지고 있는 데이터는 자신들의 서비스를 이용한 고객들의 데이터이기 때문에, 이들을 타겟으로 하는 서비스는 B금융사를 이용하던 고객들에게는 매력적이지 않을 수 있기 때문이다.
이렇게, 우리가 가진 표본들이 전체 모집단을 완벽하게 반영하지 못한다면 모델링을 아무리 잘 해도 실용성은 떨어질 수밖에 없다. 그렇지만 '완전한' 데이터를 얻을 수 없는 환경에선 어떻게 해야 할까? Robust optimization은 이에 대한 좋은 대답을 제공한다.

Robust optimization 문제의 일반적인 형태는 아래와 같다.

$\text{minimize}\,\,f_0(x)$
$\text{subject to}\,\,f_i(x, u) \leq 0\,\,\text{for all}\,\,u \in \mathcal{U},$
$i=1,2,..., m$

이는 아래의 표현과 동치이다.

$\text{minimize}\,\,f_0(x)$
$\text{subject to}\,\,\underset{u\in\mathcal{U}}{\sup} f_i(x, u) \leq 0$
$i=1,2,..., m$

일반적인 최적화 문제와 달리 constraint에 $u$라는 변수가 포함되어 있다. 최적화 문제에서 constraint는 자원의 제약을 나타낼 때가 많다고 했다. 자원의 공급에 문제가 생긴다는 것은 의사 결정 과정에 불확실성이 생긴다는 것을 의미한다. 이는 주어진 데이터가 불완정하여, 관측된 데이터 값이 실제 값과 일치하지 않을 수 있다는 뜻으로 해석할 수 있다. Robust optimization은 이 중 최악의 경우를 고려하는 문제이다. 즉 데이터의 불확실성으로 인해 constraint function의 값이 deterministic한 경우보다 커질 때, 즉 비용이 증가하는 상황일 때 그 중 최악의 경우에 맞게 목적함수를 최적화하겠다는 의미이다.
만일 현실의 의사결정에서 불확실성을 고려하지 않으면 문제가 생길 수 있다. 가령 항공사에서 오버부킹을 받았을 때, 고객들이 표를 적당히 취소해서 자리가 부족하지 않다면 항공사는 이득을 보겠지만 만일 자리가 부족해져 버리면 비행기에 타지 못한 고객들에게 손해배상을 해야 할 수도 있다. 고객들이 표를 얼마나 취소할지는 불확실성의 영역이므로, 항공사는 이를 고려해 오버부킹을 받지 않거나 매우 작은 범위 내에서만 받는 식으로 의사결정을 하는 것이 안전하다. 오버부킹을 아예 받지 않는 것은 말 그대로 최악의 경우를 고려한 100% 안전한 의사결정이고, 약간 받는 것은 100% 안전하지는 않지만 조금 더 이익을 얻을 수 있는 의사결정이다. 의사 결정자는 이 두 가지 방법 사이에서 신중하게 고민할 필요가 있으며, 이를 원하는 대로 설정할 수도 있다.

이제부터는 위의 개요를 유념하며, 다양한 robust optimization 문제의 예시에 대해 수학적으로 자세히 살펴보자.

Robust LPs

Robust optimization 문제를 풀 때 중요한 것은 uncertainty set $\mathcal{U}$를 어떻게 구성하느냐 하는 문제, 그리고 $\underset{u\in\mathcal{U}}{\sup} f_i(x, u)$를 어떻게 찾아내냐는 것이다. 모든 $\mathcal{U}$의 원소 중 최악의 경우를 찾아내는 sub-problem은 $\mathcal{U}$의 형태에 따라 다양하게 바뀔 수 있다. 가장 간단한 컨벡스 최적화 문제인 LP를 가지고 살펴보자.

Robust LPs as LPs

다음 LP 문제를 살펴보자. 이 문제는 본래 inequality constraint $m$개를 포함한 LP이지만, uncertainty set $U$를 포함하고 있다. 즉 주어진 constraint에 들어 있는 숫자가 쓰여 있는 숫자와 다르게 변화할 수 있는데, 이 변화할 수 있는 범위와 형태를 어떻게 정의하느냐에 따라 달라진다.

$\text{minimize}\,\,c^Tx$
$\text{subject to}\,\,(A+U)x \preceq b\,\,\text{for}\,\,U\in\mathcal{U}$
$x \in \mathbb{R}^n,\,A \in \mathbb{R}^{m \times n},\,b\in\mathbb{R}^m$

constraint set 중 한 부분인 $(a+u)^Tx \leq b$를 살펴보자. 만일 uncertainty set을 interval 형태로 정의하면 $||u_j||_{\infty}=\delta$라 할 때 $u_j \in [-\delta, \delta]$이므로 $\sup (a+u)^Tx=a^Tx + \delta ||x||_1$이다. 따라서 이 robust optimization 문제는 위와 같은 deterministic constraint $m$개가 모인 문제로 변형될 수 있다.

이번엔 더 일반적인 형태인 polyhedral uncertainty set을 살펴보자. 행렬 $F \in \mathbb{R}^{m \times n}$, $g \in \mathbb{R}^{m}$에 대하여 uncertainty set이 $(a + u)^T x ≤ b\,\, \text{for}\,\, u \in \mathcal{U} = \left\{u \in \mathbb{R}^n | F u + g \succeq 0\right\}$ 형태로 정의되어 있다. 이 경우 $a$의 위치가 다각형 형태로 원래에서 벗어날 수 있다는 것이므로 좀 더 실용적인 상황일 수 있지만 $\sup (a+u)^Tx$를 찾는 것이 더 까다롭다. Duality를 이용해 이 문제를 풀어 보자. Sub-problem의 라그랑지안 함수는 다음과 같다.

$L(u,\lambda) = x^Tu + \lambda^T(Fu +g)$

그리고 dual function은

$\underset{u}{\sup}\,\,L(u,\lambda) = \begin{cases} \infty\,\,\,\,\text{if}\,\,F^T\lambda + x \neq 0\\ g^T\lambda\,\,\,\,\text{if}\,\,F^T\lambda + x = 0 \end{cases}$

이다. Primal problem의 구성 요소가 전부 linear이므로 strong duality가 성립하고, 따라서
$\sup u^Tx = \inf\left\{\lambda^Tg\,|\,F^T\lambda + x = 0,\,\lambda \succeq 0 \right\}$
이다. 따라서 polyhedral uncertainty set에서의 robust LP는 $a^Tx + \lambda^Tg \leq b,\,F^T\lambda + x = 0,\,\lambda \succeq 0$의 세 equation으로 표현할 수 있으며, 따라서 몇 개의 constraint만 추가된 똑같은 LP로서 풀 수 있다.

Robust LPs as SOCPs

이번엔 norm 형태의 uncertatinty set을 살펴보자. 행렬 $P \in \mathbb{R}^{n \times m}$이 존재해서, inequality constraint가
$(a + Pu)^Tx \leq b\,\,\text{for}\,\,u\in\mathcal{U}=\left\{u\in\mathbb{R}^m\,|\,||u|| \leq 1 \right\}$로 주어졌다고 하자. 즉 $a$벡터가 행렬 $P$에 의해 변형된 norm ball 형태로 원래 값에서 벗어날 수 있다는 뜻이다. 이때 $u$에 대해 supremum을 취하면
$a^Tx + ||Px||_* \leq b$로 dual norm 형태의 constraint가 된다. 그러면, 만일 우리가 uncertainty set으로 l2 norm을 사용했을 경우 constraint는 $a^Tx + ||Px||_2 \leq b$로 SOCP 형태의 문제가 된다. Dual norm에 관해서는 https://en.wikipedia.org/wiki/Dual_norm
을 통해 리마인드 해보자.

LPs with conic uncertainty

이번엔 가장 일반적인 형태의 uncertatinty set인 conic uncertainty를 생각해 보자.
먼저 앞의 convex set 단원에서 배운 내용을 다시 살펴보면, $K \in \mathbb{R}^m$은 $x \in K$와 $t\geq0$에 대하여 $tx \in K$일 경우 cone이라고 하고, $x, y \in K$와 $\alpha, \beta > 0$에 대하여 $\alpha x + \beta y \in K$일 경우 convex cone이라고 한다. 그리고 dual cone $K^*$는 $K$의 임의의 원소 $x$에 대하여 $v^Tx \geq 0$인 벡터 $v$의 모임, 즉 $K$와 예각을 이루는 cone으로 정의된다. 그리고 $K$에 대한 generalized inequality는
$x \succeq_K y\iff x - y \in K$로 정의된다.
이제 다음과 같은 constraint를 살펴보자.

$(a+u)^Tx \leq b$
$\text{for}\,\,u\in\mathcal{U}=\left\{u\in R^n\,|\,Fu + g \succeq_K 0 \right\}$

역시 duality를 이용해 이 문제를 훨씬 간단한 문제로 변형할 수 있다. Slater's condition이 충족되었다고 할 때, $u^Tx$의 최대화 문제에 대한 라그랑지안은 $u^Tx + \lambda^T(Fu + g)$이고, dual function은

$\underset{u}{\sup}\,\,L(u,\lambda) = \begin{cases} \infty\,\,\,\,\text{if}\,\,F^T\lambda + x \neq 0\\ \lambda^Tg\,\,\,\,\text{if}\,\,F^T\lambda + x = 0 \end{cases}$

이때 strong duality에 의해
$\sup u^Tx = \inf\left\{g^T\lambda\,|\,F^T\lambda + x = 0,\,\lambda \succeq_{K^*} 0 \right\}$이고 따라서 이 robust LP는 $a^Tx + \lambda^Tg \leq b,\,F^T\lambda + x = 0,\,\lambda \succeq_{K^*} 0$의 세 equation으로 표현할 수 있다. 사실 이는 위의 polyhedral uncertainty의 경우를 generalized inequality로 확장한 것에 불과하지만, semidefinite uncertainty 등의 예시에 응용할 수 있기 때문에 유용하다.

Example: LP with semidefinite uncertainty

Symmetric matrices $A_0,\,A_1,\,...,\,A_m \in \mathbb{S}^m$과 single constraint $a^Tx \leq b$에 대해, semidefinite uncertainty를 포함한 constraint는 아래와 같다.

$(a + Pu)^Tx \leq b\,\,\text{for all}\,\,u$
$\text{s.t.}\,A_0 + \sum_{i=1}^m u_i A_i \succeq 0,\,P\in \mathbb{R}^{m \times n}$

위의 예시를 이용해 문제를 tractable form으로 바꿔 보자. Self-dual인 positive semidefinite cone $K$에 대해 interior solution $\bar{u}$ $(A_0 + \sum_{i=1}^m u_i A_i \succ 0)$가 존재한다고 가정하면 이 문제는 다음 조건을 만족하는 positive semidefinite matrix $\Lambda \succeq 0$을 찾는 것과 같다.

$a^Tx + \textbf{Tr}(\Lambda A_0) \leq b,\,\,P^T x + \begin{bmatrix} \textbf{Tr}(\Lambda A_0) \\ \vdots \\ \textbf{Tr}(\Lambda A_m) \end{bmatrix} = 0.$

Example: portfolio optimization

다음 예시를 통해 robust LP를 좀 더 잘 이해해 보자. 자산 포트폴리오를 최적화하는 문제는 리스크를 최소화 또는 원하는 만큼만 유지하면서 최대의 수익을 얻어내는 자산의 조합을 찾는 문제라고 할 수 있다. 무작위의 수익률을 가진 자산 n개라는 선택지가 있을 때, 각각의 수익률을 $R_i,\,\,i=1,\,2,\,...,\,n,\,\,E(R_i) = \mu_i$라고 하자. (편의를 위해 $\mu_1 \geq \mu_2 \geq \cdots$ 라고 하자.) 그러면 포트폴리오 최적화 문제는 아래와 같이 나타낼 수 있다.

$\text{maximize}\,\,\mu^Tx$
$\text{subject to}\,\,\mathbf{1}^Tx = 1,\,\,x\succeq 0$

당연하게도 아무 조건이 없을 때, 이 문제의 해법은 자산 1로만 포트폴리오를 구성하는 것이지만 이는 수익률의 무작위성을 무시하는 위험한 결정이다. 만일 우리가 각 자산의 수익률이 $\mu_i \pm u_i,\,\,u_1 \geq u_2 \geq \cdots \geq u_n = 0$의 변동성을 가졌다는 것을 안다고 가정해보자. 이는 기대 수익률이 높은 자산일수록 위험도도 크다는 가정이므로 비교적 현실적이다. (마지막 자산은 리스크가 없는 안전 자산이라고 생각하자.) 그러면 이 문제는 아래와 같이 다시 표현된다.

$\text{maximize}\,\,\sum_{i=1}^n \underset{u \in [-u_i, u_i]}{\inf}(\mu_i + u)x_i$
$\text{subject to}\,\,\mathbf{1}^Tx = 1,\,\,x\succeq 0$

이때 목적함수를 $\mu^Tx - \sum_{i=1}^n |u_i| x_i$로 쉽게 바꿀 수 있다. 우리가 불확실성을 고려하지 않을 경우 자산 1에 모든 돈을 투자하여 약 50%의 확률로 큰 수익을 얻거나 큰 손해를 보겠지만, 불확실성을 고려하지 않을 경우 수익 규모는 작아져도 작은 리스크로 이를 보장받을 수 있다. 원하는 수익 규모가 클수록 큰 리스크를 감수해야 한다는 사실을 기억하자.

수익률의 기댓값과 변동성을 $\mu_i = 1.05 + 0.3/i,\, R_i \in [\mu_i - 0.6/i,\, \mu_i + 0.6/i]$ 으로 설정한 다음 최적화하면 $x_n$에 모든 돈을 투자하라는 결론이 나온다. 이는 우리가 리스크를 전혀 지지 않는 선택을 했기 때문이다. 변동성 $u$를 일정 값을 넘어가게 설정하는 순간 항상 이런 결과가 도출되며, 안전한 은행 예금에 모든 돈을 넣어 두는 것으로 비유할 수 있다.

이번에는 같은 문제에서 리스크를 조금 감수하는 선택을 해 보자. 다시 말해 높은 확률($1-\epsilon$)로 보장받을 수 있는 최대의 수익을 찾아내는 것이다. 수식으로 표현하면 다음과 같다.

$\text{maximize}\,\,t$
$\text{subject to}\,\,\mathbb{P}(\sum_{i=1}^n R_ix_i \geq t) \geq 1-\epsilon$

이 문제는 풀기 어려운 non-convex 문제지만, 앞의 statistical estimation 세션에서 배운 내용을 이용해 convex 문제로 approximation할 수 있다. $R_i$는 $-u_i \leq R_i \leq u_i$로 bound된 random variable이다. 따라서 hoeffiding's inequality를 적용하면 $t \geq 0,\,x \in \mathbb{R}^n$에 대해 아래의 probability bound를 도출할 수 있다. (참고: https://en.wikipedia.org/wiki/Hoeffding%27s_inequality)

$\mathbb{P}\left(\sum_{i=1}^n (R_i - \mu_i)x_i \leq -t \right) \leq \exp\left(-\frac{t^2}{2\sum_{i=1}^n x_i^2u_i^2}\right)$

이를 조금 변형하면,
$\mathbb{P}\left[\sum_{i=1}^n R_ix_i \leq \mu^Tx -t \left(\sum_{i=1}^n u_i^2x_i^2 \right)\right] \leq \exp\left(-\frac{t^2}{2}\right)$
여기에서 $t = \sqrt{2 \log \frac{1}{\epsilon}}$을 선택하면 $\sum_{i=1}^n R_ix_i \geq \mu^T x - \sqrt{2 \log \frac{1}{\epsilon}} ||\text{diag}(u)x||_2$ 가 최소 $1-\epsilon$의 확률로 보장됨을 확인할 수 있다. 따라서 이 최적화 문제는 다음과 같이 재표현될 수 있다.

$\text{maximize}\,\,\mu^Tx - \sqrt{2 \log \frac{1}{\epsilon}} ||\text{diag}(u)x||_2$
$\text{subject to}\,\,\mathbf{1}^Tx = 1,\,\,x\succeq 0$

이 문제는 uncertatinty set을
$\mathcal{U} = \left\{u \in \mathbb{R}^n\,|\,||\text{diag}(u)^{-1/2}u||_2 \leq \sqrt{2 \log \frac{1}{\epsilon}} \right\}$
와 같이 설정한 SOCP이다. 이 기준으로 문제를 다시 풀어 보면, 5%의 수익을 100% 확실히 보장받을 수 있던 아까와 달리 최소 9%의 수익을 최소 99.98% 확률로 보장받을 수 있다는 훨씬 유용한 결과가 도출된다.

아래 코드를 통해 cvxpy 패키지를 이용한 계산 결과를 확인해볼 수 있다.

import numpy as np
import matplotlib.pyplot as plt
import cvxpy as cp
%config InlineBackend.figure_format='retina'

np.random.seed(1)

n = 200
mu = 1.05 + 0.3 * np.linspace(1, 1/n, n)
u_max = 0.05 + 0.6 * np.linspace(1, 1/n, n)  # Uncertainty sets
u_max[-1] = 0  # No variability on the last coordinate
epsilon = 2e-4  # Risk parameter (probability of failure)

x_nom = np.concatenate(([1], np.zeros(n-1)))  # Nominal solution (best return)
x_con = np.concatenate((np.zeros(n-1), [1]))  # Conservative solution

x_rob_cvx = cp.Variable(n)
z_cvx = cp.Variable(n)
t_cvx = cp.Variable(1)

# Define the objective function
objective = cp.Maximize(mu @ x_rob_cvx - t_cvx)

# Define the constraints
constraints = [
    cp.sqrt(2 * cp.log(1/epsilon)) * cp.norm(z_cvx, 'fro') <= t_cvx,
    z_cvx == cp.multiply(u_max, x_rob_cvx),
    cp.sum(x_rob_cvx) == 1,
    x_rob_cvx >= 0
]

# Create the problem with objective and constraints
port_prob = cp.Problem(objective, constraints)

port_prob.solve(solver=cp.ECOS, max_iters=100, verbose=False)

x_rob = x_rob_cvx.value

num_samples = 2 * 10**4
returns_nom = np.zeros(num_samples)
returns_con = np.zeros(num_samples)
returns_rob = np.zeros(num_samples)
for sample in range(num_samples):
    R = mu + u_max * (1 - 2 * np.random.rand(n))
    returns_nom[sample] = np.sum(R * x_nom)
    returns_con[sample] = np.sum(R * x_con)
    returns_rob[sample] = np.sum(R * x_rob)

print("Value at risk", epsilon, "is at least",
      np.sum(mu @ x_rob) - np.sqrt(2 * np.log(1/epsilon)) * np.linalg.norm(u_max * x_rob))

plt.figure()

plt.hist(returns_nom, bins=16, color=[0.5, 0.4, 1], label="x_nom")
plt.hist(returns_con, bins=[mu[n-1]-1e-2, mu[n-1] + 1e-2], color=[0.9, 0.6, 0.4], label="x_con")
plt.hist(returns_rob, bins=14, color=[0.1, 0.1, 0.8], label="x_eps")
plt.axis([0.6, 2, 0, num_samples/2])
plt.legend()
plt.show()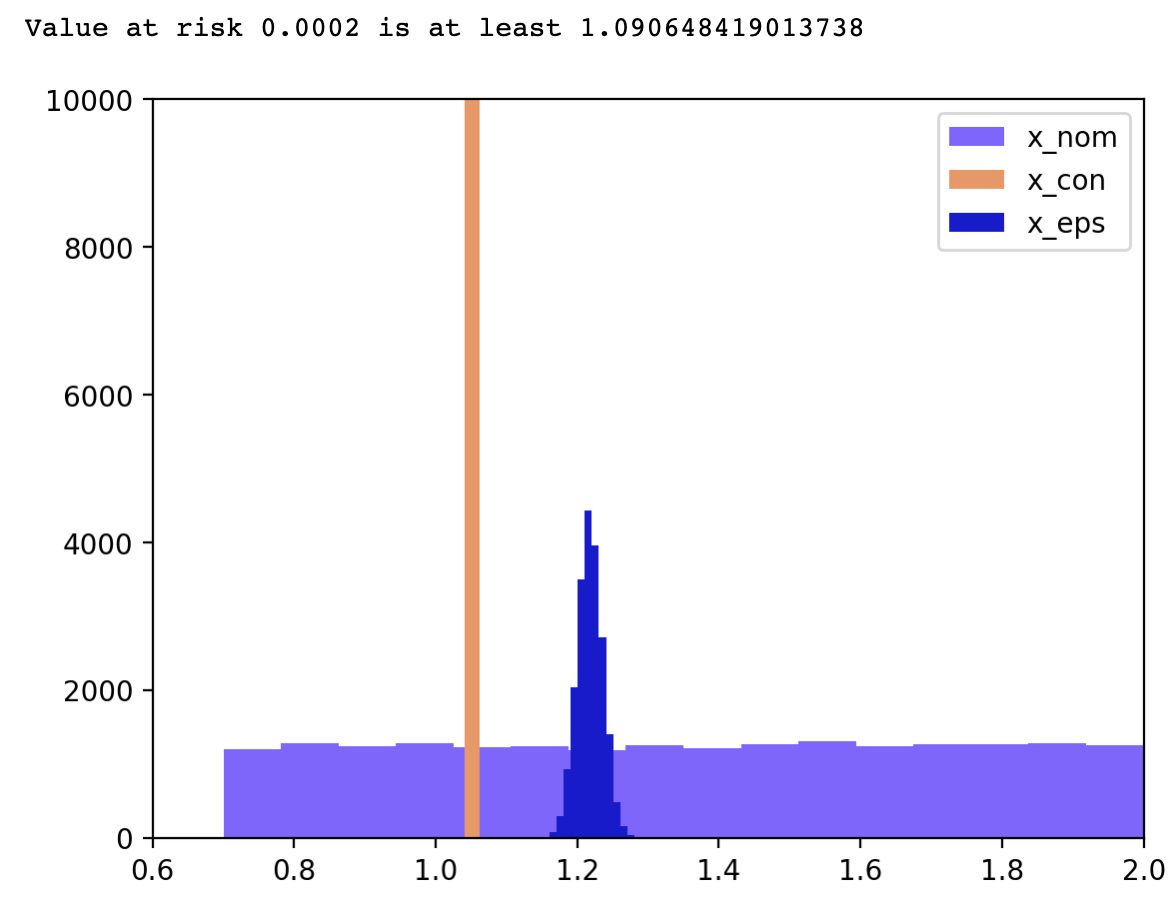

10000번 샘플링 시의 결과. x_nom은 non-robust한 경우, x_con은 리스크를 지지 않을 때, x_eps은 $\epsilon$만큼의 리스크를 감수할 때이다.