[논문 스터디] iSAM2: Incremental Smoothing and Mapping Using the Bayes Tree

Estelle Yoon·2025년 3월 18일

Study

목록 보기

3/8

Bibtex 인용

@INPROCEEDINGS{5979641,
  author={Kaess, Michael and Johannsson, Hordur and Roberts, Richard and Ila, Viorela and Leonard, John and Dellaert, Frank},
  booktitle={2011 IEEE International Conference on Robotics and Automation}, 
  title={iSAM2: Incremental smoothing and mapping with fluid relinearization and incremental variable reordering}, 
  year={2011},
  volume={},
  number={},
  pages={3281-3288},
  keywords={Simultaneous localization and mapping;Graphical models;Smoothing methods;Sparse matrices;Accuracy;Trajectory},
  doi={10.1109/ICRA.2011.5979641}}

요약

기존의 그래픽 베이스 모델 추론 알고리즘과 sparse matrix factorization method의 연결을 이해하기 위한 기초를 제공
- bayes tree라는 새로운 구조를 통해 제공
Clique tree와 유사하지만 방향성을 가지는 bayes tree를 제시
SLAM 문제의 squre root information matrix에 더 자연스럽게 mapping

인트로

Probabilistic inference algorithm
- 다양한 로봇 공학 분야에서 활용 ex) SLAM, tracking, etc
본 연구는 large-scale SLAM에 집중
센서의 불확실성 때문에 probabilistic inference algorithm이 선호됨

기여

Bayes tree라는 새로운 데이터 구조를 제안
- matrix factorization을 bayes net으로 변환 가능
- QR factorization의 결과가 더 natural하게 mapping됨
- 구조를 conditional probabilistic density로 분석 가능
iSAM2라는 새로운 알고리즘을 개발함
- Incremental variable re-ordering과 fluid re-linearization, periodic batch step의 제거를 통한 efficiency 개선
- sparse non-linear problem에 효율적 solution
- bayes tree기반 영향을 받는 부분만 re-calculate → 효율성 증대
- 실시간성 확보

Problem

Target

non-linear한 추정 문제에 대해 incremental하고 real-time인 해결 방법
- incremental: 새로운 measurement가 추가될 때 마다 추정값을 업데이트 현재 측정된 모든 값으로 도출할 수 있는 가장 정확한 환경모델 반영
- real-time: 작업을 수행하는 동안 추정값을 실시간 제공, 탐색 및 계획을 위한 추정값 필요
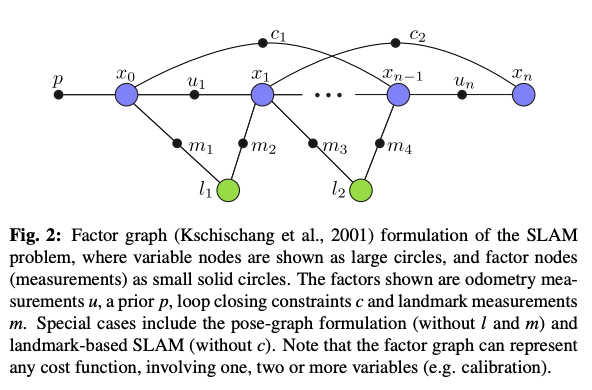
주어진 추정 문제를 그래프 모델로 표현하기 위해 factor graph사용
- 다양한 확률 분포나 비용 함수를 포함할 수 있음
- factor node - 랜드마크 측정값, 오도메트리(움직임에 관한 정보), loop closing constraint(재방문 시 발생하는 제약조건) 등
- variable node - 추정하려는 변수, 각 시간 스텝에서의 위치, 랜드마크의 위치 등

Gaussian Case

non-linear least squre 문제
- $\arg\min_{\Theta} \frac{1}{2} \sum_{i} \lVert h_i(\Theta_i) - z_i \rVert^2_{\Sigma_i}$
  - $h_i$ - measurement function
  - $z_i$ - measurement
  - $|| e ||^2_Σ = e^T Σ^(-1) e$ - mahalanobis distance
linearization
- gauss-newton, levenberg-marquardt
- 각 iteration에서 linearization point $\theta$ 부근에서 테일러 전개를 수행 새로운 least squre 문제를 도출
- $argmin_Δ || AΔ - b ||^2$
- $A$ - measurement jacobian
- linearization 됐으니까 새로운 추정값은 단순 +로 계산가능
$A \Delta - b$ 의 최소 해는 Cholesky 혹은 QR factorization 을 통해 계산
iSAM2는 QR factorization 사용
- incrementally update square root information matrix
- measurement 추가 시에 matrix variable의 순서가 최적이 아니게 되고 fill-in현상이 발생할 수 있음
  - periodic batch re-ordering을 수행하고 batch factorization 진행
  - iSAM과 다르게 re-linearization은 batch 단계에서만 수행
  - period of batch step은 heuristically(empirically인듯?

The Bayes Tree

기존의 factor graph를 sparse matrix로 바꾸어 sparse linear algebra대신 graph model 자체에서 연산을 수행

Inference and Elimination

추정은 factor graph를 bayes net으로 변환하는 것으로 이해할 수 있음
변수 제거 $P(\Theta) = \prod_{j} P(\theta_j | S_j)$
- $S_j$ 는 $\theta _j$ 와 직접 연결된 변수들의 집합
factor graph 변환 과정

- 위의 과정을 반복하여 모든 variable을 제거하면 bayes net이 됨
- probabilistically variable의 probability의 곱이 conditional probability의 곱으로 변환된는 것과 같음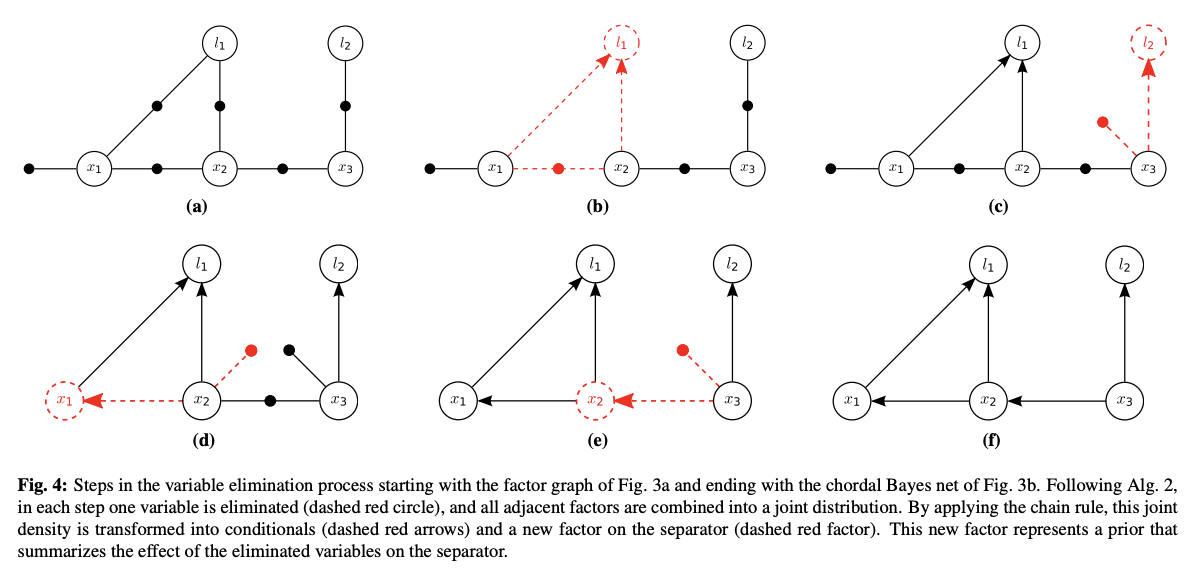

위에 그림이 이해가 좀 안됨

보조 강의

모두 제거하고 나면 all factor들이 conditional probability로 표현가능해짐, tree structure를 가지게 됨
- 이것이 부분적으로 새로운 measurement에 대해 inference할 수 있게하는 핵심 요소

Gaussian Case

elimination 과정이 sparse QR factorization of measurement jacobian과 같음
factor에 대한 gaussian density는 $f_{\text{joint}}(\Delta_j, s_j) \propto \exp \left( -\frac{1}{2} \left\| a \Delta_j + A_S s_j - b \right\|^2 \right)$ 로 정의
- $A_j = [a | A_S]$ - $\Delta _j$ 에 연결된 모든 요인의 partial derivatives를 concat한 matrix
bayes tree로 변환할 때 사용되는 conditional probability는 $P(\Delta_j | s_j) \propto \exp \left( -\frac{1}{2} (\Delta_j + r s_j - d)^2 \right)$
- $r = a^\dagger A_S , ~d =a^\dagger b$
- $a^\dagger$ 는 $a^T a$ 의 pseudo-inverse matrix
- $a$ - $\Delta$ 와 관련된 factor의 일부, partial derivative
- $b$ - $\Delta$ 와 관련된 measurements
- $d$ - $a^\dagger b$
- $A_S$ - $S_j$ 의 partial derivatives 집합
- $S_j$ - seperator; $\theta_j$ 와 직접 연결된 variable
새로운 factor는 $f_{\text{new}}(s_j) = \exp \left( -\frac{1}{2} \left\| A'_0 s_j - b'_0 \right\|^2 \right)$
- $A_0 ' = A_S - ar ,~ b'_0 = b-ad$
이 과정은 gram-schmidt의 한 단계, 밀도 형태로 해석됨
sparse vector $\gamma$ 와 scalar $d$ 는 bayes net의 single joint conditional density를 지정하거나 sparse information matrix의 하나의 행
least square problem은 tree의 leaves to root방향으로 한 번 통과하면서 최적의 $\Delta ^*$ 를 계산, root to leaf 로 내려가며 각 변수의 최적 할당을 구함 → backsubstitution

Creating Bayes Tree

Bayes tree
- linear algebra와의 equivalence를 더 잘 표현
- 새로운 recursive algorithm을 가능하게 함
- chordal 구조 - 모든 부분 순환 구조의 크기가 3이하, 4 이상이면 현을 가져야함
- 최적화 및 marginalization에 용이
- 방향성을 가지고, factored probability density를 encode하는 방식
- 각 node에 대해 $P(\Theta) = \prod_k P(F_k | S_k)$ conditional density 정의
  - $S_k$ - 클리크 $C_k$ 와 부모 클리크 $\Pi_k$ 의 intersection
  - $F_k$ - 나머지 변수들

Gaussian Case

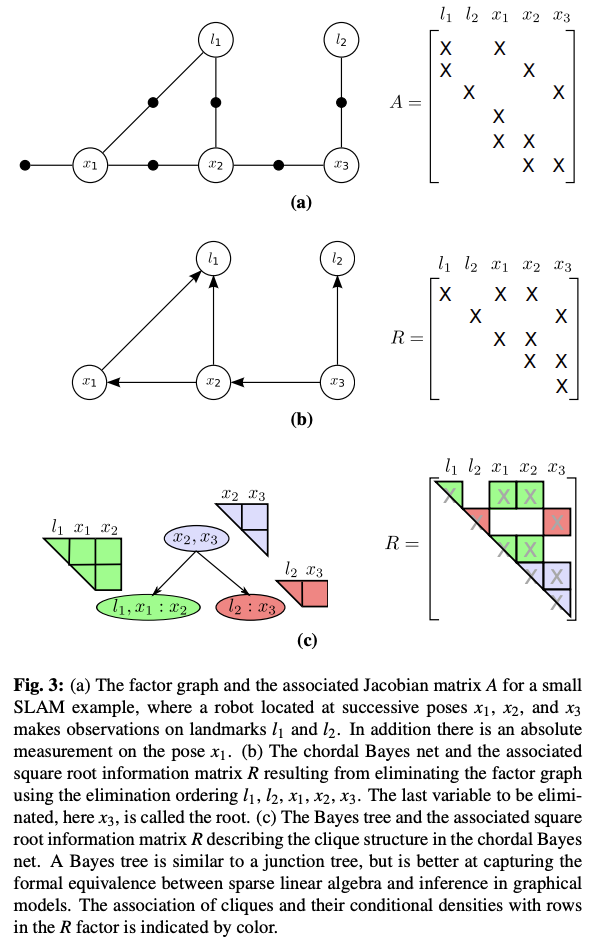
하나의 bayes tree가 여러 다른 square root information factor에 대응할 수 있음
- 임의의 순서가 매겨지기 때문
- 전체 variable의 순서는 fill-in이나 수치에 영향주지 않고 matrix내의 위치에만 영향

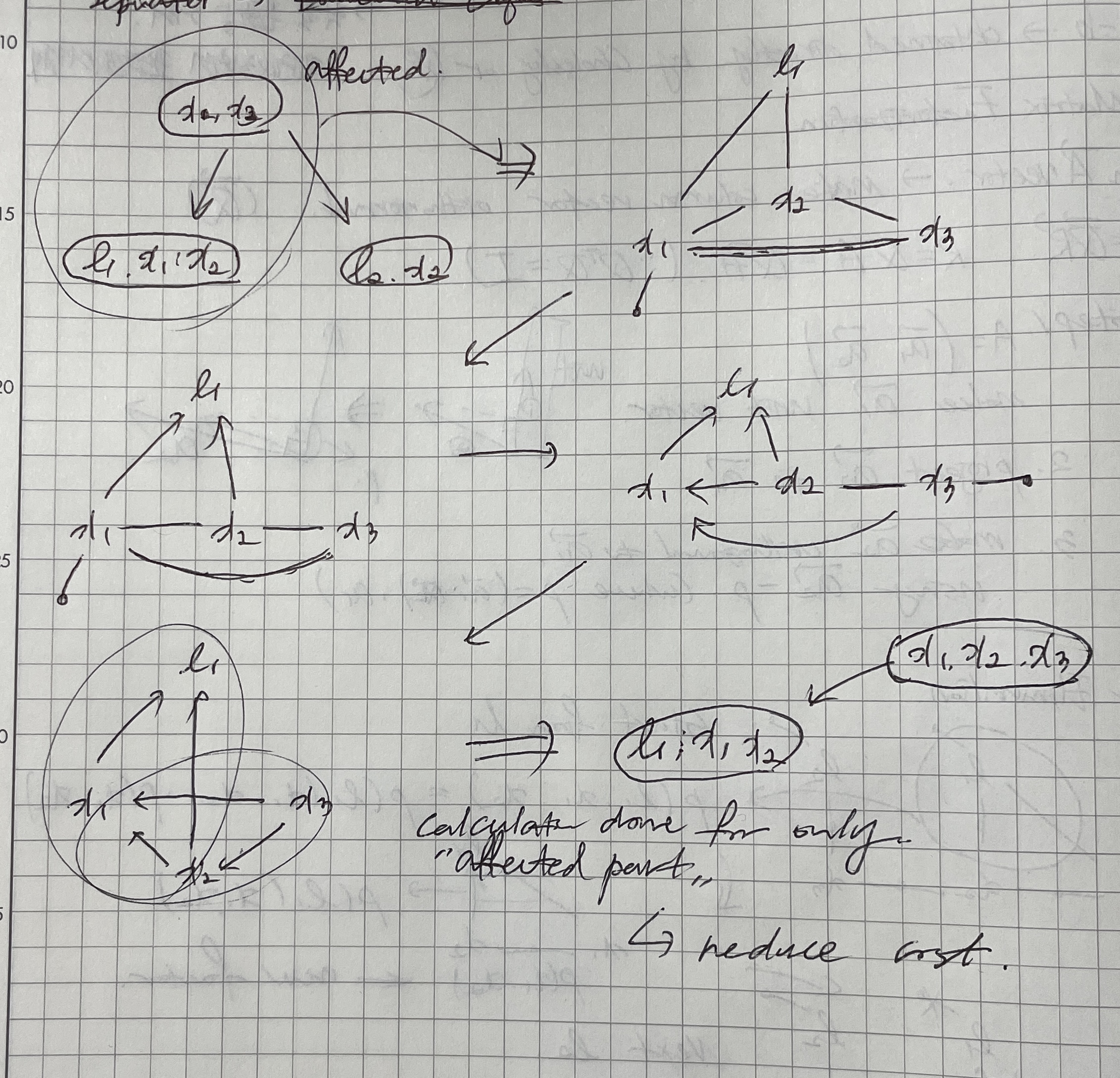
Incremental Inference

inference 영상

incremental inference는 간단한 트리 수정으로 가능
영향을 받는 clique와 root사이의 경로만 영향을 받음 (clique to root , root to clique)
new factor가 추가되므로, 다시 eliminating process를 거침

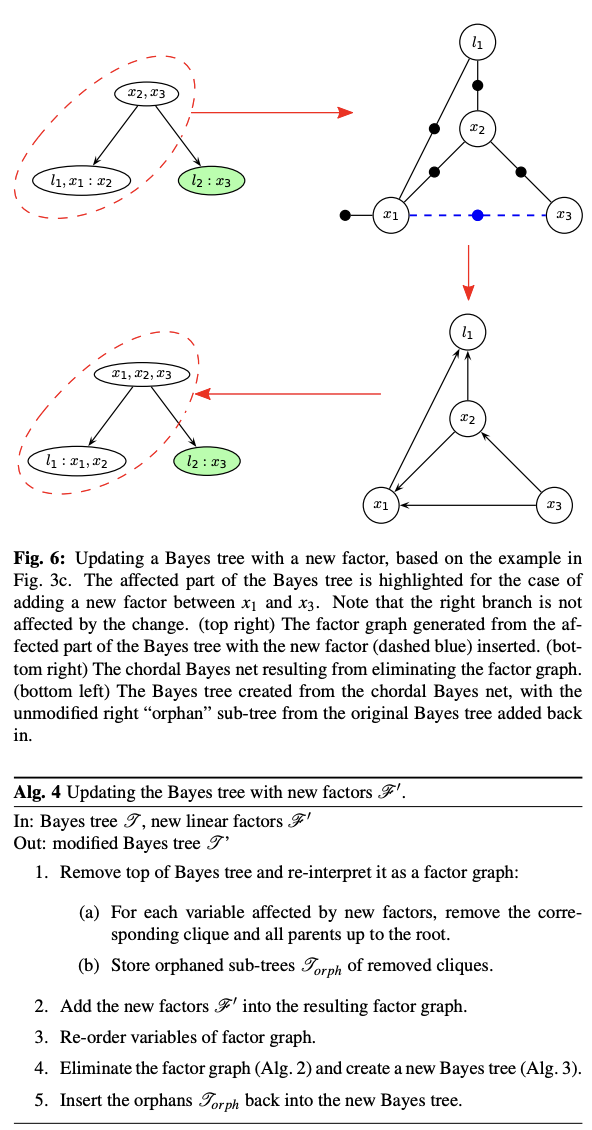
사진 이해 잘 안됨

Incremental Variable Ordering

variable ordering은 sparse matrix solution에 필수적
square root information matrix의 추가 항목인 fill in 최소화를 위해 optimal order가 추구됨
chordal 상황 제외 fill in은 불가피함
- NP-hard, COLAMD등을 통해 optimal한 순서 찾기 가능
incremental inference 시에, 각 update 마다 variable update가능
- iSAM에서 사용한 periodic batch reordering 불필요
- bayes tree에서 partial variable reordering을 수행
  - globally optimal하지는 않지만 locally optimal한 값을 제공
tree 구조가 가지는 장점에 대한 예시

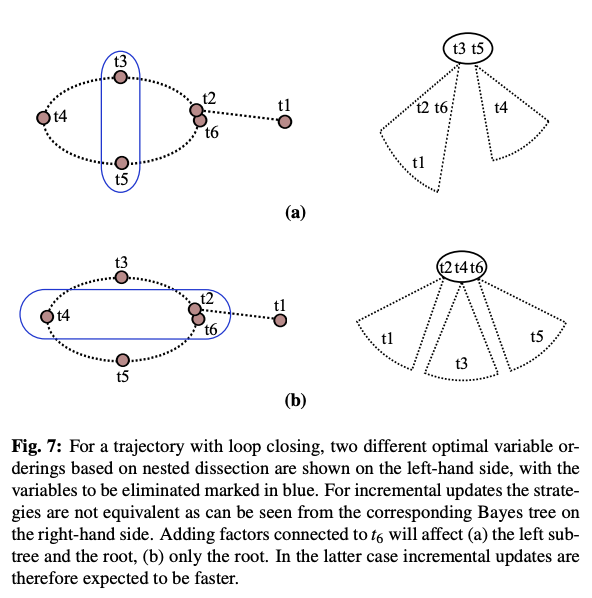
measurement를 통합하는데 발생하는 비용은 root에 가까워 질수록 작아짐
COLAMD와 같은 휴리스틱을 locally 사용하면 현재단계의 fill in만을 고려하는 한계 존재
- 가장 최근 접근한 variable을 끝 순서로 배치하는 incremental ordering 제안
incremental ordering
- constrained COLAMD 사용, most recent variable을 강제로 끝 순서에 배치하면서도 globally 준수한 order를 유지
- 이후 업데이트 시에 영향을 받는 부분을 작게 유지할 수 있는 방법
- 다만 큰 loop closing 발생시 예외적으로 비용이 큼

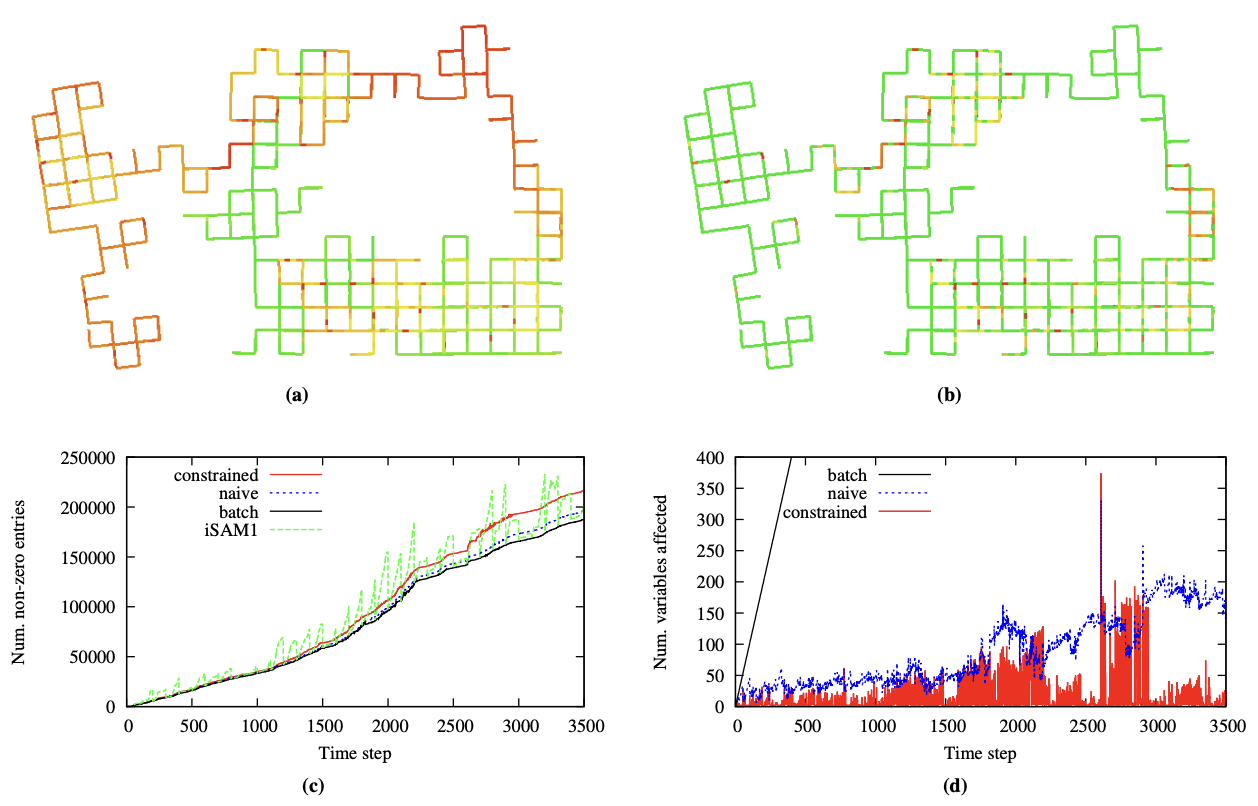
- batch보다 나음 - 당연하지 않나
- 특정 구간에서 급격한 fill in의 증가 - 아마도 loop closing 때문

The iSAM2 Algorithm

non-linear factor 처리 → 기존의 bayes tree는 linear만 다룸
fluid re-linearization → 필요한 부분만 partially linearization수행 cost를 줄이고 효율성을 향상
partial state update → 실제 변화가 있는 factor들에 대해서만 update 수행

Fluid Relinearization

linearization 필요성 판단
- 현재 추정값이 linearization point를 벗어날 경우
- 임계값 이상의 변화가 발생할 경우
bayes tree 의 부분적 수정
- linearization을 수행하는 변수와 관련된 정보만 제거하여 partial relinearization 수행
marginal factor 계산
- relinearization 과정에서 발생한 eliminated sub-tree 정보를 상위단으로 전달
- caching시에 tree의 중간에서 부터 다시 계산도 가능

Partial State Update

update partially, 변경된 변수만 계산 → computational cost 감소
top tree만 변경되므로 sub-tree로는 제한적으로 propagate
특정 clique의 variable의 $\Delta$ 변화량이 임계치 이하면 업데이트 중지
- 해당 clique의 sub tree variable의 변경이 없음이 보장됨
nearly exact solution 유지 가능

Algorithm and Complexity

algorithm
- 변수 집합 추정
- incremental non-linear factor $F$ 고려
- 새로운 factor, variable이 계속 추가돔
- bayes tree 활용 최적화 수행
- 선형화 시스템 반복적 해결 방식
complexity
- general case
  - gauss-newton 방식 사용
  - 최소점 근처에서 quadratic convergence
- exploration task
  - 각 pose마다 constrain 존재
  - 영향을 받는 factor가 상수개 → $O(1)$
- loop closure
  - general case → full factorization 필요 → $O(n^3 )$
  - under certain assumption → backsubstitution → $O(n^{1.5} )$
- emperical complexity
  - 이론적 상한보다 훨씬 낮음
  - 매 단계에서 대부분 partially compute/refactorization수행하므로 대부분의 경우 효율적 계산

Estelle Yoon

Studying

이전 포스트

[논문스터디] SuMa++: Efficient LiDAR-based Semantic SLAM

다음 포스트

[논문 스터디] iSAM2: Incremental Smoothing and Mapping Using the Bayes Tree

Study

Bibtex 인용

요약

인트로

관련 연구

기여

Problem

Target

Gaussian Case

The Bayes Tree

Inference and Elimination

Creating Bayes Tree

Incremental Inference

Incremental Variable Ordering

The iSAM2 Algorithm

Fluid Relinearization

Partial State Update

Algorithm and Complexity

[논문스터디] SuMa++: Efficient LiDAR-based Semantic SLAM

[논문스터디] KPConv: Flexible and Deformable Convolution for Point Clouds

0개의 댓글