GAN

논문 : https://arxiv.org/pdf/1406.2661.pdf

᭼ 0. Abstract

번역:

• 이 논문은 Generative Adversarial Networks(GANs)라는 새로운 기계 학습 프레임워크를 제시합니다.
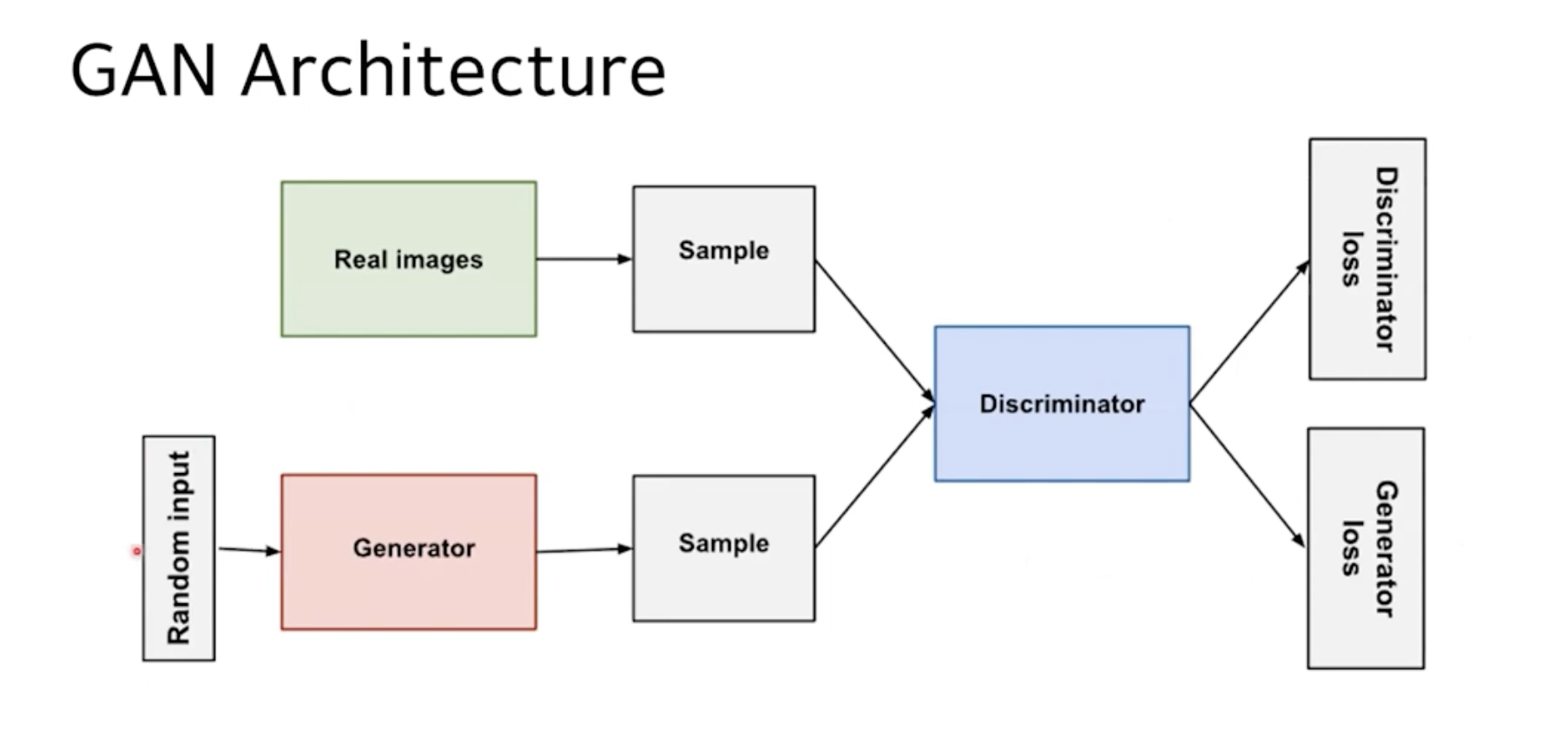
• 이 프레임워크에서 생성기(generator)는 데이터의 실제 분포를 모사하려고 시도하고, 판별기(discriminator)는 생성기가 생성한 가짜 데이터와 실제 데이터를 구별하려고 시도합니다.
• 이 둘은 적대적 게임 설정에서 서로 경쟁하며, 생성기는 판별기를 속이는 능력을, 판별기는 가짜 데이터를 식별하는 능력을 향상시킵니다.
• 실험은 Generator가 얼마나 실제와 가까운 이미지를 생성했는지에 대한 질적 및 정량적 평가를 통해 이 framework의 잠재력을 입증함.

᭼ 1. Introduction

번역 :

문단 1)

• 딥러닝의 잠재된 가치 : 다양한 종류의 데이터에 대한 확률 분포를 나타내는, 풍부하고 계층적인 모델을 발견하는 것.
  ex.) 자연 이미지, 음성을 포함하는 audio wave 폼, 자연어 말뭉치의 기호 등.
  지금까지 딥러닝의 가장 성공 사례 - 고차원의 풍부한 센서 입력 -> 클래스 레이블[14, 22] 로 매핑하는 판별 모델들에 기반함.
  ㄴ 이러한 성공들은 주로 backpropagation, dropout 알고리즘을 사용. , using piecewise linear units(조각 선형 유닛) [19, 9, 10] which have a particularly well-behaved gradient(잘 동작하는 기울기를 갖는)
• 하지만, Deep "Generative" model의 경우
  1. approximating many intractable probabilistic computations that arise in maximum likelihood estimation and related strategies
  : 최대 likelihood 추정과, 관련된 전략들에서 나오는 다양한 다루기 어려운 확률적 계산들을 근사하기 어렵고
  2. generative context에서, piecewise linear units의 장점을 활용하기 어려움.
  때문에 덜 영향력 있었음.
  

따라서 이러한 어려움을 우회하는 새로운 생성 모델 추정 절차를 제안합니다.

문단 2)
제안된 adversarial nets 에서 생성 모델은 adversary(적대자)와 맞붙게 됨.
이 적대자는, 샘플이 모델 분포에서 왔는지 데이터 분포에서 왔는지 모델 분포에서 왔는지 판단하는 판별 모델로써 학습됨.
위조지폐 <-> 경찰 의 개념으로 설명.
양측 팀 모두, 위조물이 진품과 구별할 수 없을 정도로 자신들의 방법을 개선하도록 만듦.

문단 3)
이 프레임워크는, 다양한 종류의 모델과 최적화 알고리즘에 대해 특정한 훈련 알고리즘을 도출할 수 있음.
이 논문에서는,
생성 모델 - 랜덤 노이즈를 다층 퍼셉트론을 통과시켜 샘플을 생성하고,
판별 모델 - 얘도 다층 퍼셉트론.
인 특수한 경우를 탐구함. 이 특수한 경우를 적대적 신경망(adversarial nets)이라고 함.
이 경우, 우리는 역전파, 드롭아웃 알고리즘만을 사용하여 두 모델을 모두 훈련 시킬 수 있으며,
생성 모델에서는 순방향 전파만을 사용하여 샘플링할 수 있음.
근사 추론이나 마르코프 체인이 필요하지 않음.

᭼ 2. Related Work

이 부분은 논문에서 '관련 연구(Related Work)'라는 섹션을 다루고 있습니다. 이 부분은 연구자들이 GAN이라는 새로운 모델을 제안하는 배경에 대한 정보를 제공하며, 이전에 개발되고 사용된 여러 가지 생성 모델과 비교 분석을 통해 GAN의 독특한 접근 방식과 이점을 강조합니다.
이 섹션은 GAN이 이전의 모델과 어떻게 다르고, 왜 이러한 차이가 중요한지를 설명함으로써, 독자가 이 연구의 중요성을 이해하는데 도움을 줍니다.

요약하면, 이 섹션에서는 다음의 주요 주제들을 다룹니다:

잠재 변수를 가진 지향성 그래픽 모델 대안에 대한 설명: 여기에는 제한된 볼츠만 머신(RBMs), 깊은 볼츠만 머신(DBMs) 등이 포함되며, 이러한 모델들의 확률 밀도 계산의 어려움이 언급됩니다.

깊은 신념 네트워크(DBNs)의 설명과 그 특성: 이 모델은 지향성 그래픽 모델과 비지향성 그래픽 모델의 특성을 모두 갖습니다.

로그-우도를 근사하거나 제한하지 않는 대체 기준에 대한 언급: 스코어 매칭과 노이즈-대조적 추정(NCE) 등이 여기에 해당하며, 이러한 방법들은 확률 밀도를 분석적으로 지정해야 합니다.

확률 분포를 명시적으로 정의하지 않고 원하는 분포로부터 샘플을 추출하는 생성기를 학습시키는 접근법: 이 방법은 역전파를 통해 기계를 학습시킬 수 있음을 보여줍니다. 이런 방법론에는 생성적 확률 네트워크(GSN) 프레임워크 등이 있습니다.

적대적 네트워크(GAN)의 독특한 점: 마르코프 체인이 필요 없으며, 피드백 루프를 요구하지 않아 단조 선형 유닛을 더 잘 활용할 수 있다는 점이 이 부분에서 강조됩니다.

이러한 내용을 통해, 이 섹션은 GAN이 기존의 다양한 생성 모델과 어떻게 다르며, 어떤 새로운 가치를 제공하는지를 명확하게 보여줍니다. 이는 이 논문의 핵심 주장인 새로운 생성 모델 'GAN'의 독창성과 중요성을 강조하고 있습니다.

1. RBMs, DBMs, 및 이들의 변형들
   : 잠재 변수를 가진 무향(undirected) 그래피컬 모델.

   • 비정규화된 잠재함수들의 곱으로 나타내어지며, 랜덤 변수들의 모든 상태에 대한 전역 합산/적분으로 정규화됨.
   • 이 quantity(partition function)과 이 기울기는, 가장 간단한 경우를 빼고는 모두 계산하기 어렵고, 마르코프 체인 몬테 카를로 (MCMC) 방법을 통해 추정될 수 있음.
   • 하지만 이 MCMC에 의존하는 학습 알고리즘들은 mixing 이라는 중요한 문제를 야기함.

2. DBNs

   • undirected layer(무향 층) 하나랑, 여러 개의 directed layer를 포함하는 혼합 모델.
   • 빠른 근사 층별 훈련 기준이 존재하지만, 무향 및 유향 모델과 관련된 계산 어려움을 겪음.

3. score matching, noise-contrasive estimation (NCE)

   • 로그 가능도(log-likelihood)를 근사하거나 제한하는 것이 아닌 대안적인 기준들.
   • 이 두가지 방법은, 학습된 확률 밀도가 정규화 상수까지 분석적으로 지정되어야 함. 하지만, 여러 레이어의 잠재 변수가 있는 생성 모델 (ex. DBNs , DBMs)에서는 처리 가능한 비정규화 확률 밀도를 유도하는 것이 불가능할 수 있음.
   • NCE에서는 별도의 판별 모델을 맞추는 대신, 생성 모델 자체가 고정된 잡음 분포에서 생성된 데이터(위조 지폐)와, 샘플을 구분하기까지 함. 이 경우 학습 속도가 급격히 느려짐.

4. 확률 분포를 명시적으로 정의하지 않고 원하는 분포로부터 샘플을 추출하는 생성기를 학습시키는 접근법

   • 이 방식은 backpropagation을 통해 훈련될 수 있도록 설계할 수 있어 좋지만, parameterized Markov chain을 정의힘. 즉, generative 마르코프 체인의 한 단계를 수행하는 기계의 매개변수를 학습함.

-> 이에 비해, GAN은 샘플링에 마르코프 체인이 필요하지 않음. 또, 피드백 루프를 요구하지 않아 단조 선형 유닛(piecewise linear unit)을 더 잘 활용할 수 있다는 점이 이 부분에서 강조됩니다.
: 마르코프 체인은 다양한 알고리즘과 모델에 사용되지만, 몇 가지 문제점이 있습니다.

수렴 시간: 마르코프 체인을 사용하는 모델은 마르코프 체인이 수렴하는데 시간이 걸립니다. 즉, 적절한 결과를 얻기 위해서는 마르코프 체인을 많은 단계 동안 실행해야 하는데, 이는 상당한 계산 비용을 발생시킵니다.

수렴 확인: 마르코프 체인이 실제로 수렴했는지를 판단하는 것이 어렵습니다. 이는 알고리즘이 적절한 결과를 만들어내고 있는지 확인하기 어렵다는 의미입니다.

미분 불가능: 많은 최적화 기법들이 그래디언트 기반인데, 마르코프 체인을 통한 샘플링 과정은 일반적으로 미분이 불가능합니다. 따라서, 이러한 모델들을 효과적으로 학습시키기 위한 방법이 제한적입니다.

상태 의존성: 마르코프 체인은 현재 상태에만 의존하는 성질이 있습니다. 이는 체인이 장기적인 종속성을 가지는 데이터를 모델링하는 데 제한적일 수 있다는 것을 의미합니다.

이에 반해, GAN은 샘플링에 마르코프 체인이 필요하지 않습니다. 이는 모델 학습과 샘플 생성이 더욱 빠르고 효율적이며, 더욱 간단한 프레임워크 내에서 이루어질 수 있음을 의미합니다. 또한, GAN의 생성 모델은 직접적으로 데이터 공간에 대해 작동하며, 이는 샘플들 사이의 장기적인 종속성을 더 잘 캡처할 수 있음을 의미합니다.

: 피드백 루프(feedback loop)를 요구하지 않는다는 것은, 생성 네트워크가 출력을 생성한 후에 이를 다시 입력으로 사용하지 않는다는 것을 의미합니다. 피드백 루프가 있을 경우, 네트워크는 이전의 출력에 기반한 새로운 출력을 생성합니다. 이러한 구조는 재귀적인 구조를 가질 수 있고, 시간에 따라 변화하는 데이터를 처리하는 데 유용할 수 있지만, 각 단계에서 오류가 누적되는 문제가 발생할 수 있습니다.

반면에, GAN은 직접적인 전진 경로(forward path)만을 가집니다. 생성 네트워크는 랜덤 노이즈를 입력으로 받아, 데이터를 생성하는 함수를 학습하고, 이 함수는 그래디언트 역전파를 통해 효율적으로 학습될 수 있습니다.

이러한 접근 방식에서 단조 선형 유닛(piecewise linear units)이 잘 작동한다는 점은 중요합니다. 이러한 유닛들은 ReLU(Rectified Linear Unit)나 Leaky ReLU와 같은 활성화 함수를 의미하는데, 이들은 비선형 함수에 비해 계산이 간단하고 그래디언트 소실 문제를 줄이는 데 도움이 됩니다. 그러나, 이들은 미분 가능한 값이 0 또는 양수로 제한되므로, 피드백 루프가 있는 구조에서는 활성화 값이 무한히 증가하는 문제(unbounded activation)가 발생할 수 있습니다.

따라서, GAN이 피드백 루프를 요구하지 않기 때문에, 이러한 단조 선형 유닛을 효과적으로 사용할 수 있으며, 이를 통해 효율적인 학습과 높은 성능을 달성할 수 있습니다.

이러한 내용을 통해, 이 섹션은 GAN이 기존의 다양한 생성 모델과 어떻게 다르며, 어떤 새로운 가치를 제공하는지를 명확하게 보여줍니다. 이는 이 논문의 핵심 주장인 새로운 생성 모델 'GAN'의 독창성과 중요성을 강조하고 있습니다.

᭼ 3. Adversarial nets

᭼ 4. Theoretical Results

- 4.1 Global Optimality of pg = pdata

- 4.2 Convergence of Algorithm 1

᭼ 5. Experiments

᭼ 6. Advantages and disadvantages

᭼ 7. Conclusions and future work