이번 글은 내 캐릭터의 발이 돌을 뚫고 들어갔어요의 심화버전입니다. 해당 글을 읽지 않아도 글의 내용을 이해하는데 문제는 없지만, 유니티에서 Foot IK를 내장함수로 간단하게 구현하고 싶으신 분은 위 글을 보시는걸 추천드립니다.

IK(Inverse Kinematics)란

---

게임 속 모든 동작을 미리 애니메이션 데이터로 제작하는 것은 현실적으로 불가능하다. 예를 들어, 다양한 높이의 계단을 오르거나 불규칙한 지형을 걷는 경우, 애니메이션을 정해진 데이터로만 처리하면 발이 공중에 뜨거나 지형을 뚫는 등의 문제가 발생할 수 있다.

이를 해결하기 위해 실시간으로 본(Bone)의 움직임을 조정하는 절차적 애니메이션(Procedural Animation) 기법이 사용된다. 그중 가장 대표적인 방법이 IK(Inverse Kinematics, 역운동학) 이다. IK는 엔드 이펙터(End Effector, 손이나 발과 같은 본의 끝 부분)의 목표 위치를 설정하면, 이를 만족하는 본의 회전 값을 자동으로 계산하는 기법이다.

이와 반대되는 개념으로는 FK(Forward Kinematics, 순방향 운동학)가 있는데 두 방식을 비교해보자.

• FK: 부모 본의 회전을 직접 제어하여 자식 본이 따라가도록 설정하는 방식.
• IK: 목표 위치(예: 손, 발)를 기준으로 본들의 회전 값을 자동으로 계산하는 방식.

실제 게임에서는 IK를 활용하여 애니메이션을 보정함으로써 더 자연스러운 동작을 만들 수 있다. 예를 들어 캐릭터가 걷거나 뛰는 애니메이션에서 발이 지형을 따라가도록 자동 조정하거나, 컵이나 총과 같은 물체 자연스럽게 들기, 주먹의 타격 지점을 정확한 곳으로 옮기는 방식 등으로 응용하여 사용할 수 있다.

(윗 짤처럼 캐릭터에게 총을 잡게 하려면 Hand IK의 적절한 이용이 필요하다)

IK 모델링

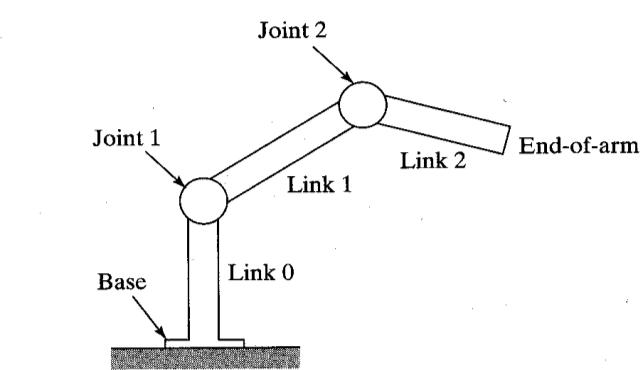
IK시스템에서는 주로 joint를 기준으로 회전과 포지션을 정의한다.

• child가 없는 joint들을 end-effector라고 한다.
• 모든 joint들은 parent-child를 사용하며, 유니티의 Transform처럼 parent joint가 바뀌면 child joint도 영향을 받는다.
• IK에서는 체인 위주의 변화가 일어나며 체인 외의 joint들은 크게 변하지 않는다.(예를 들어 왼손의 IK를 적용한다고 오른손의 본 상태가 크게 바뀌지 않는다)

이에 따라 아래에서는 각 joint들을 Effector, IK 계산시 서로 영향을 받는 joint들을 묶어 IKChain으로 이름을 붙여 구현할 것이다.

2. 유니티 에서의 휴머노이드

---

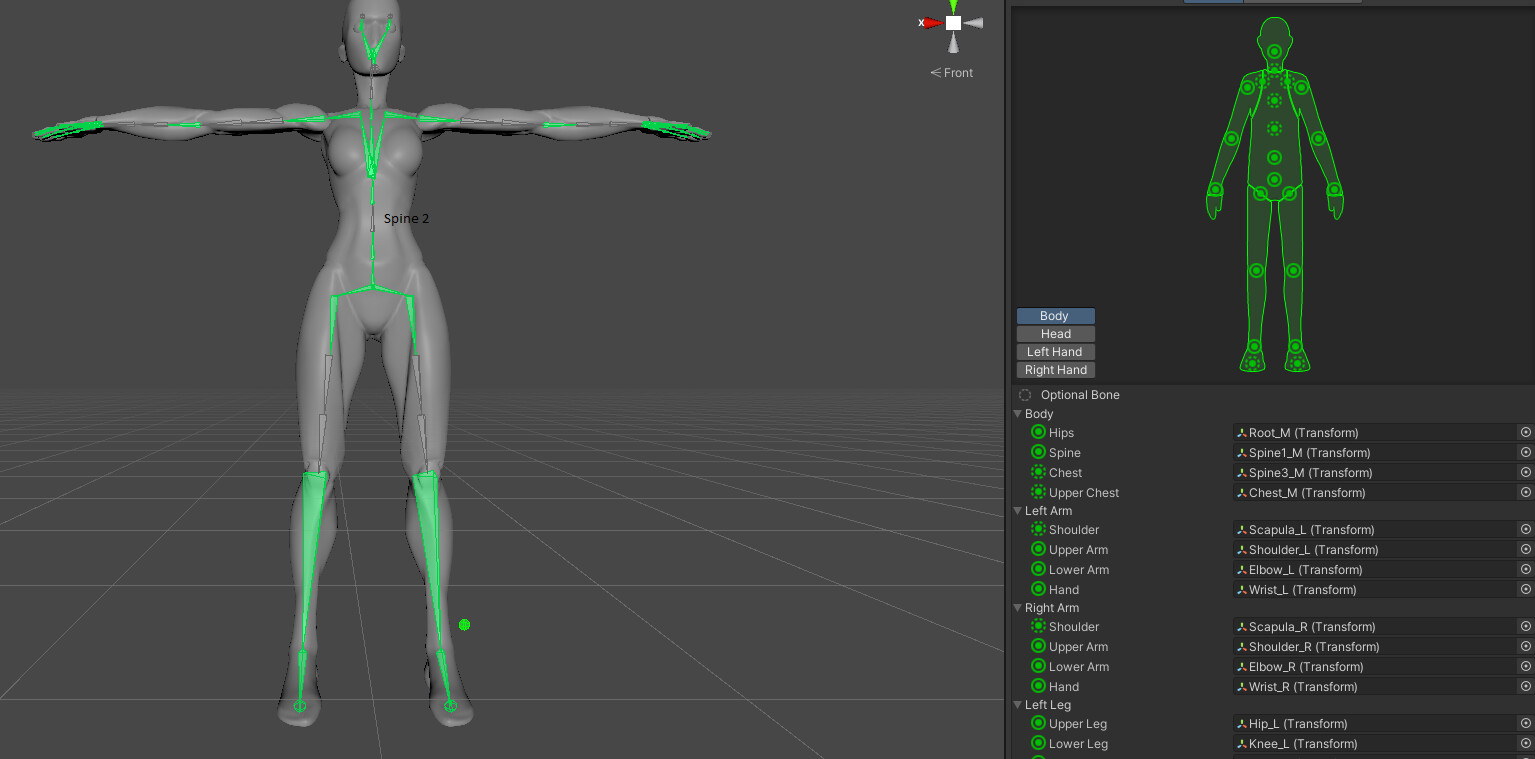
(사진 출처: Ongoing humanoid issues in Animation Rigging)

게임 속 캐릭터의 본 구조는 휴머노이드(Humanoid) 아바타를 기반으로 제작되는 경우가 많다. Unity의 Humanoid Rig는 사람이 가지는 기본적인 본 구조를 정의한 표준 구조이며 일반적으로 게임 제작에서 가장 많이 사용되는 아바타의 유형이라고 볼 수 있다. 아는 사람은 다 아는 Mixamo에서는 실제 사람의 움직임을 모션캡쳐한 휴머노이드 아바타의 애니메이션을들 다운 받을 수 있다. 캐릭터의 애니메이션을 만들 때에는 주로 이러한 모션 캡쳐 데이터에 IK등을 통한 후처리로 자연스러운 애니메이션을 만들어 게임에 적용한다고 보면 된다.

휴머노이드 아바타의 특징

(사진 출처: Unity:UsingHumanoidChars)

Unity의 Humanoid Rig는 인간 골격을 기반으로 설계된 표준 본 구조를 제공하며, 모션 캡처 데이터 및 IK 시스템과 결합하여 자연스러운 애니메이션을 생성할 수 있도록 설계되었다. 일반적으로 모델링, 리깅(Rigging), 스키닝(Skinning)의 과정을 거쳐 Unity의 애니메이션 시스템에서 사용된다.

Humanoid 모델의 기본 구조

• 휴머노이드 모델은 실제 인간 골격과 유사한 최소 15개 이상의 본(Bone)으로 구성된다.
• 주요 본 구조:
  • Hips (골반) → Spine (척추) → Chest (가슴) → Neck (목) → Head (머리)
  • Hips (골반) → UpperLeg (허벅지) → Leg (정강이) → Foot (발) → Toe (발가락)
  • Chest (가슴) → Shoulder (어깨) → Arm (팔) → Forearm (팔뚝) → Hand (손)
• 이러한 구조는 Unity의 Avatar 시스템과 매칭되며, 자동으로 본을 매핑하여 적용할 수 있음.
• 팔과 다리는 2개씩 있으므로 일관성이 있는 명명 규칙을 사용해야 함 (예: 왼팔은 “arm_L”, 오른팔은 “arm_R”)
• T-포즈(T-Pose) 또는 A-포즈(A-Pose)로 모델링하는 것이 일반적.

• 머리, 상체, 팔, 다리 등 필수적인 본(Bone) 계층이 포함되어 있다.
• IK를 적용할 때, 제약 조건(Constraints)을 고려해야 현실적인 움직임을 만들 수 있음.

그래픽스에서 사용하는 human body는 수많은 joint들로 이루어져 있고, 이들은 서로 다른 DoF(Degree of Freedom)와 Restriction(해당 본은 어느 범위 안에서만 회전 가능 등등..)을 가지고 있다.

휴머노이드 IK 적용 시 제약 조건

IK는 자유롭게 본을 움직일 수 있지만, 현실적인 움직임을 위해서는 물리적 제약을 추가해야 한다.

관절의 자연스러운 각도 제한

• 인간의 관절은 일정한 범위를 넘어서는 회전이 불가능하다.
• 예: 팔꿈치는 뒤쪽으로 꺾일 수 없으며, 무릎도 특정 각도 이상 접히지 않는다.

본들의 충돌 방지

• 관절이 서로 겹치는 비현실적인 동작을 방지해야 한다.
• 예: 손이 허리를 통과하는 모션이 나오지 않도록 함.

3. IK 기법들 비교

---

IK는 다양한 수학적 기법들을 통해 구현할 수 있다. 대표적인 기법인 CCD, FABRIK, 자코비안 행렬기반 세 가지를 비교해보겠다.

자코비안 행렬

가장 기본적인 접근법으로 자코비안 행렬을 계산하여 선형 근사하는 방법이다. 로봇공학 등에서 많이 사용하는 해석적/수치적 방법으로, 자코비안 행렬을 이용하여 관절 각도의 변화를 계산한다. 엔드 이펙터의 위치 변화와 관절 각도 변화 사이의 관계를 나타내는 Jacobian 행렬 (J)을 구성한 뒤, 목표와 현재의 위치 차이를 줄이도록 (J)의 역행렬(또는 의사역행렬)을 사용해 각도 변화 ($\Delta$ $\Theta$)를 계산한다.

• 가장 일반성이 높은 방법으로 관절 개수, 관절 구조, 다중 end-effector등 복잡한 시스템도 통일된 수학적 틀로 풀 수 있다. Joint에 한계나 추가 목표를 반영하려면 목적함수에 제약을 추가하거나 DLS방식으로 가중치를 주는 등 확장이 용이하다.
• 정밀한 제어가 가능하며 오차를 매우 작게 줄일 수 있다.
• 계산 비용이 크고 구현 난이도가 높다. 관절 수가 많으면 (J)가 커지고 매 프레임 행렬 연산 (역행렬)을 해야 하므로, 실시간 게임에선 부담이 될 수 있다. 특히 3D 캐릭터에 수십 개 관절이 있을 경우 자코비안 계산은 비효율적일 수 있다.

일반적으로 실시간 게임에서는 잘 활용되지 않는 방법이지만 로봇 시뮬레이션 등에는 활용하고 있으며, 유니티 엔진에서는 ArticulationJacobian와 같은 PhysicsModule API가 제공되기도 한다.

CCD

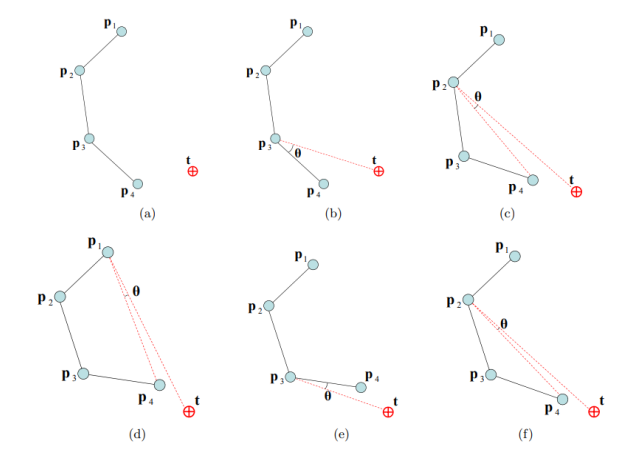
FABRIK 등장 이전에 많이 쓰이던 방식이다. CCD는 순환 좌표 하강법이라는 이름 그대로, 관절을 하나씩 순차적으로 조정하여 end effector(말단 연골 또는 말단 부위)이 목표에 다가가도록 하는 휴리스틱 방법이다. 체인의 끝 관절부터 시작하여 거꾸로(base 방향) 각 관절을 차례로 회전시켜 end effector가 목표 위치에 최대한 가까워지도록 반복한다.

• 각 반복(iteration)에서 가장 끝 관절(end effector에 가장 가까운 관절)을 목표 방향으로 회전시켜 end effector를 목표에 근접시킨 후, 그 다음 관절로 이동해 같은 작업을 수행한다. 이러한 역순으로의 반복적인 각도 조절을 통해 오차를 점차 줄여나간다.
• 수학적으로는 특별한 행렬 계산 없이, 기하학적 각도 계산만으로 구현된다. 예를 들어 각 관절에서, end effector와 목표를 잇는 벡터 사이의 각도를 계산하고, 그 각도만큼 관절을 회전시키는 식이다.
• 이러한 작업을 만족스러운 값이 나올 때 까지 반복하며, 구현이 간단하고 비용이 적기 때문에 실시간 IK에서 활용할 수 있다.
• 단점으로는 많은 반복이 필요할 수 있고, 관절이 많은 체인이거나 초기 오차가 큰 경우 목표에 도달하기 위한 반복 횟수가 많아질 수 있다.

FABRIK

FABRIK는 Forward And Backward Reaching Inverse Kinematics의 약자로, 전진-후진 반복을 통해 관절 위치를 계산하는 기법이다. CCD처럼 반복적이지만, 각 단계에서 회전 각도가 아닌 관절의 위치를 직접 계산한다는 차이가 있다. 알고리듬은 다음 두 단계로 이루어진 한 번의 iteration을 반복한다. FABRIK은 언리얼에서는 유니티에서도 주로 사용하고 있는 기법이다.

• 수학적 처리: FABRIK는 주로 벡터 산술과 거리 계산으로 이루어진다. 각 관절 간의 거리(d_i)를 초기 설정 때 저장해두고, 알고리즘 진행 중에는 정규화된 방향 벡터를 따라 해당 거리만큼 점을 이동시키는 계산을 반복합니다. 복잡한 행렬 연산 없이 기하학적으로 위치를 결정하는 방식이다.
• 목표 도달 가능 여부: 알고리즘 첫 단계에서 목표가 reachable한지 검사한다. 루트에서 목표까지의 거리와 모든 뼈 길이의 합을 비교하여, 목표가 사슬 최대 길이보다 멀면 도달 불가능하다고 판단한다. 이 경우 FABRIK은 체인을 목표 방향으로 최대한 뻗은 직선 형태로 배치하고 종료한다(end effector는 목표에는 못 미치지만 최대한 가까워짐)

Foward

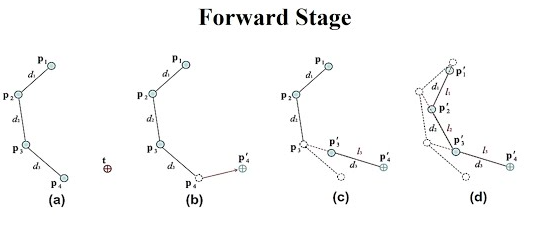
체인의 end effector를 목표 위치로 바로 이동시킨 후, 끝역방향으로 차례로 관절들을 재배치한다. 이 때 뼈의 길이를 보존해야 하므로, 자식 관절의 새 위치로부터 본래 길이만큼 떨어진 지점에 상위 관절을 배치한다. 이렇게 하면 end effector부터 루트까지 관절들이 목표 쪽으로 끌려온다.

Backward

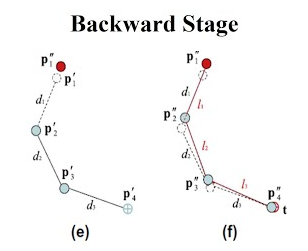
Backward 단계가 끝나면 체인의 루트 관절을 원래 위치로 돌려놓는다. 그리고 이제 순방향(루트→말단)으로 진행하면서, 방금 정한 루트 위치로부터 차례로 자식 관절들을 뼈 길이를 유지하며 배치합니다. 즉, 루트에서 2번째 관절을 루트로부터 제자리 뼈 길이만큼 떨어진 곳에 놓고, 그 다음 관절도 이전 관절로부터 일정 거리 떨어뜨리는 식으로 end effector까지 진행합니다.

반복

위와 같은 과정을 원하는 지정된 횟수만큼 반복한다. 중간에 오차범위가 원하는 범위까지 좁혀지면 반복을 그만둘 수도 있다.

🔗 유튜브 영상: FABRIK IK 알고리즘 개요
🔗 IK 알고리즘 비교 및 FABRIK 설명

FABRIK의 장단점

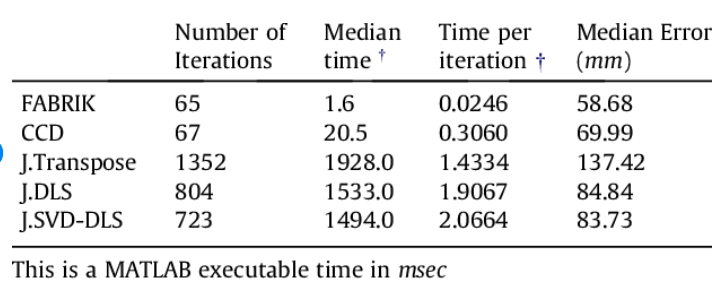
자료출처: FABRIK: A fast, iterative solver for the Inverse Kinematics problem

장점:

• 수렴 속도가 빠르고 안정적이다. 논문 결과 FABRIK은 CCD보다 약 10배 빠르고, 자코비안 기반 방법보다 1000배 빠르다고 보고되었다.
• 구현이 비교적 쉽고 범용적이다. 각 단계가 단순한 거리 계산과 보간으로 이뤄져 있어 이해하기 쉬우며, 임의 길이와 구조의 체인에도 적용 가능하다.
• 다중 end-effector 확장이 가능하다. 휴머노이드 캐릭터처럼 여러 개의 말단(손, 발 등)을 가진 모델에도 FABRIK은 확장된 알고리즘으로 대응할 수 있다.

단점:

• 관절 회전 제한을 고려하지 않는다는 한계가 있다. FABRIK은 거리만 유지하며 위치를 옮기기 때문에, 관절이 가질 수 없는 각도로 배치될 수도 있다.
• 목표에 매우 근접하게 수렴하기 위해서는 반복이 필요하다. 1~2번의 iteration으로 대강의 자세는 나오지만 오차를 수 픽셀 이하로 줄이려면 여러 번 더 반복해야 한다. 반복 계산 자체는 가볍지만 리얼타임 렌더러에서 프레임 단위로 많은 IK를 풀 때는 이 역시 고려해야 한다.

4. 유니티에서 FABRIK 적용

---

유니티의 Humanoid 시스템과 Animation시스템과 연동될 수 있도록 클래스들을 구현하였다. 기존 오브젝트에 추가적인 컴포넌트를 추가하지 않고 필드 하나(HumanoidFabrk)만 추가하여 동작하도록 해보았다. 구현한 클래스에대한 설명이다.

1. HumanoidFabrik

HumanoidFabrik 클래스는 Humanoid 모델에 FABRIK IK를 적용하기 위한 인터페이스이자 IK 솔버 관리 클래스이다. IK 체인들과 effector들을 통합 관리하며, 각 프레임에 IK 계산을 수행하는 중앙 제어 역할을 한다.

2. FabrikChain

FabrikChain 클래스는 하나의 관절 체인에 대해 FABRIK 알고리즘을 적용하는 IK 솔버 클래스이다. 이 클래스는 한 개의 end effector와 그것에 이르는 일련의 관절들을 나타내며, FABRIK 수식을 실제로 계산하여 관절들의 새로운 위치를 결정한다.

• IK 과정

  1. 초기 상태 갱신:

     • $\mathbf{p}_i$ : 각 본의 초기(루트 공간) 위치
     • $L_i$ : 인접 본 사이의 링크 길이
     • $\mathbf{d}_i$ : 각 본의 초기 자식 방향 (즉, $\mathbf{p}_{i+1} - \mathbf{p}_i$)
     • $\mathbf{R}_i$ : 각 본의 초기 회전 (루트 공간 기준)

  2. 목표와의 거리 확인:

     • 만약 목표 $\mathbf{t}$ 와 루트 본 사이의 거리가 전체 체인 길이보다 크면, 본들을 단순하게 늘린다.

  3. 반복적 Forward-Backward 과정:

     • Backward 단계:

       • 마지막 본(엔드 이펙터)를 $\mathbf{p}_n \gets \mathbf{t}$ 로 고정한 후,
         $i = n-1$ 부터 $i = 1$ 까지 아래의 수식으로 업데이트

         $\mathbf{p}_i \gets \mathbf{p}_{i+1} + L_i \cdot \frac{\mathbf{p}_i - \mathbf{p}_{i+1}}{\|\mathbf{p}_i - \mathbf{p}_{i+1}\|}$

     • Forward 단계:

       • 루트 본($i = 0$)의 위치는 고정한 채, $i = 1$ 부터 $i = n$ 까지 업데이트

         $\mathbf{p}_i \gets \mathbf{p}_{i-1} + L_{i-1} \cdot \frac{\mathbf{p}_i - \mathbf{p}_{i-1}}{\|\mathbf{p}_i - \mathbf{p}_{i-1}\|}$

     • 오차 $\|\mathbf{p}_n - \mathbf{t}\|^2$ 가 미리 정한 $\Delta^2$ 이하가 될 때까지 반복

3. HumanoidFabrikEffector

FABRIK 체인을 구성할 때, 트랜스폼 값의 저장과 부모-자식 관계를 나타내는 역할을 수행한다.

4.1. 코드분석

0. Humanoid Util

public static class HumanoidUtils
{
    private static readonly Dictionary<HumanBodyBones, HumanBodyBones> HumanBodyBonesParentMap = new()
    {
        // Hips → Spine → Chest → Neck → Head
        { HumanBodyBones.Spine, HumanBodyBones.Hips },
        { HumanBodyBones.Chest, HumanBodyBones.Spine },
        { HumanBodyBones.Neck, HumanBodyBones.Chest },
        { HumanBodyBones.Head, HumanBodyBones.Neck },

        // Hips → UpperLeg → LowerLeg → Foot → Toes
        { HumanBodyBones.LeftUpperLeg, HumanBodyBones.Hips },
        { HumanBodyBones.LeftLowerLeg, HumanBodyBones.LeftUpperLeg },
        { HumanBodyBones.LeftFoot, HumanBodyBones.LeftLowerLeg },

        { HumanBodyBones.RightUpperLeg, HumanBodyBones.Hips },
        { HumanBodyBones.RightLowerLeg, HumanBodyBones.RightUpperLeg },
        { HumanBodyBones.RightFoot, HumanBodyBones.RightLowerLeg },

        // Spine - Chest - Shoulders - Arm - Forearm - Hand
        // UpperChest는 인덱스 문제로 사용하지 않음
        // { HumanBodyBones.UpperChest, HumanBodyBones.Chest },

        { HumanBodyBones.LeftShoulder, HumanBodyBones.Chest /* UpperChest */ },
        { HumanBodyBones.LeftUpperArm, HumanBodyBones.LeftShoulder },
        { HumanBodyBones.LeftLowerArm, HumanBodyBones.LeftUpperArm },
        { HumanBodyBones.LeftHand, HumanBodyBones.LeftLowerArm },

        { HumanBodyBones.RightShoulder, HumanBodyBones.Chest /* UpperChest */ },
        { HumanBodyBones.RightUpperArm, HumanBodyBones.RightShoulder },
        { HumanBodyBones.RightLowerArm, HumanBodyBones.RightUpperArm },
        { HumanBodyBones.RightHand, HumanBodyBones.RightLowerArm },
    };

	
    public static readonly Dictionary<HumanBodyBones, List<HumanBodyBones>?> HumanBodyBonesChildrenMap = new()
    {
        { HumanBodyBones.Hips, new List<HumanBodyBones> { HumanBodyBones.Spine, HumanBodyBones.LeftUpperLeg, HumanBodyBones.RightUpperLeg } },
        { HumanBodyBones.Spine, new List<HumanBodyBones> { HumanBodyBones.Chest } },
        { HumanBodyBones.Chest, new List<HumanBodyBones> { HumanBodyBones.Neck, HumanBodyBones.LeftShoulder, HumanBodyBones.RightShoulder } },
        { HumanBodyBones.Neck, new List<HumanBodyBones> { HumanBodyBones.Head } },
        // HumanBodyBonesParentMap 관계를 역으로 저장
        ...
    };

    public static readonly SortedSet<HumanBodyBones> IkEffectorBones = new()
    {
        HumanBodyBones.Hips,
        HumanBodyBones.Spine,
        // 위 dict에서 사용하는 bone들을 저장
        ...
    };
    ...
}

휴머노이드 본을 어떻게 해석하고 체인을 구성할지에 대한 값들이 저장된 데이터를 HumanoidUtils클래스에 저장해두었다. 본들의 연결 구조는 위 #Humanoid 모델의 기본 구조 챕터의 내용을 참고하여 구성하였다.

유니티의 enum class인 HumanBodyBones를 분석해보니 휴머노이드 아바타에서의 본은 부모본보다 value가 크게 설정되어 있는 것으로 보여 enum value의 값을 비교하여 부모본인지 아닌지 체크할 수 있게 구성해보았다.

(이상하게도 UpperChest는 예외적으로 큰 값이 설정되어 있어 해당 본은 제외하였다)

1. HumanoidFabrik

public class HumanoidFabrik
{
    private Animator _animator;

	private readonly Dictionary<HumanBodyBones, HumanoidFabrikEffector> _effectors = new();
	private readonly Dictionary<HumanBodyBones, FabrikChain> _endChains = new();
	private readonly List<FabrikChain> _chains = new();

	public void Initialize(Animator animator)
	{
		_animator = animator;

		InitializeEffectors(animator);
		var rootEffector = _effectors[HumanBodyBones.Hips];

		_rootChain = LoadSystem(rootEffector);
		_chains.Sort((x, y) => y.Layer.CompareTo(x.Layer));
	}
    ....
}

Humanoid Fabrik은 루트인 Hips본을 시작으로 각 본에 해당하는 Effector와 IK를 기반으로 본들의 트랜스폼을 계산할 Chain을 초기화한다. 각 이펙터들은 _effectors 딕셔너리에 Bone을 키로 접근할 수 있도록 초기화된다. 이후 LoadSystem 메서드를 호출하여 각 체인들을 초기화하고 Layer순으로 오름차순 정렬을 시도한다.

private FabrikChain LoadSystem(HumanoidFabrikEffector effector, FabrikChain parent = null, int layer = 0)
{
	var effectors = new List<HumanoidFabrikEffector>();
	if (parent != null)
		effectors.Add(parent.EndEffector);
	List<HumanBodyBones> childrenBones = null;
	while (effector != null)
	{
		childrenBones = HumanoidUtils.GetChildrenBones(effector.Bone);
		effectors.Add(effector);
		if (childrenBones == null)
			break;
		// childCount > 1 is a new sub-base
		if (childrenBones.Count != 1)
			break;
			effector = _effectors[childrenBones[0]];
	}
	var chain = new FabrikChain(effectors, layer, _animator, _effectors);
	_chains.Add(chain);
    
	if (chain.IsEndChain)
		_endChains.Add(chain.EndEffector.Bone, chain);
	else if (childrenBones != null)
		foreach (var child in childrenBones)
			LoadSystem(_effectors[child], chain, layer + 1);
		return chain;
}

체인을 초기화하는 LoadSystem함수이다. _endChains에는 EndEffector의 Bone을 기준으로 각 체인에 접근할 수 있게 초기화 되며, 초기화 과정은 아래 그림과 같다.

붉은 원은 사용하는 본들 중에서 여러 개의 Sub-System으로 분리되는 부분이고, 파란 원은 사용하는 본들중에서 EndBone에 해당하는 부분이다. 초기화는 Hips부터 시작되므로, Hips-Chain이 Layer 0값을 가지고 초기화되며, 이후 다른 Sub-System으로 분리되는 체인들은 전부 Layer1의 값을 가진다. 이후 Chest에서 다시 한번 Sub-System으로 분리되어 생성되는 체인은 Layer2값을 갖는다. 이를 정리하면 아래와 같다.

• hips chaine - Layer 0
• Right Foot - Layer 1 end
• Left Foot - Layer 1 end
• Chest - Layer 1
• RightHand - Layer 2 end
• LeftHand -Layer 2 end
• Head - Layer 2 end

만약 Eye본이나 손가락과 관련된 본도 제어하는 경우 더 많은 Layer와 end chain들이 생성될 것이며 현재 구현을 사용하기 위해 end-chain과 관련된 로직들을 변경해서 사용해야 할 것이다.

이러한 시스템이 성공적으로 초기화 되면, IK Target을 설정하고 Solve IK 함수를 호출하여 원하는 포지션에 End Bone을 위치시키고, End Bone의 체인에 포함된 본들이 자연스럽게 조정될 수 있을 것이다.

2. FabrikChain

public FabrikChain(List<HumanoidFabrikEffector> effectors, int layer, Animator animator, IReadOnlyDictionary<HumanBodyBones, HumanoidFabrikEffector> dictionary)
{
	...
	//initial array
	Bones              = new Transform[ChainLength + 1];
	Positions          = new Vector3[ChainLength + 1];
	BonesLength        = new float[ChainLength];
	StartDirectionSucc = new Vector3[ChainLength + 1];
	StartRotationBone  = new Quaternion[ChainLength + 1];
	...

	// Init Pole
	...

	//init data
	var current = EndEffector;
	CompleteLength = 0;
	for (var i = Bones.Length - 1; i >= 0; i--)
	{
		Bones[i]             = current.Transform;
		StartRotationBone[i] = GetRotationRootSpace(current.Transform);

		if (i == Bones.Length - 1)
		{
			//leaf
			StartDirectionSucc[i] = GetPositionRootSpace(Target) - GetPositionRootSpace(current.Transform);
		}
		else
		{
			//mid bone
			StartDirectionSucc[i] =  GetPositionRootSpace(Bones[i + 1]) - GetPositionRootSpace(current.Transform);
			BonesLength[i]        =  StartDirectionSucc[i].magnitude;
			CompleteLength        += BonesLength[i];
		}

		var parent = HumanoidUtils.GetParentBone(current.Bone);
		if (parent == HumanBodyBones.LastBone)
			break;
		current = dictionary[parent];
	}
}

생성자에서는 체인에게 사용하는 어레이들을 초기화하는 부분을 집중해서 보면 될 것 같다.

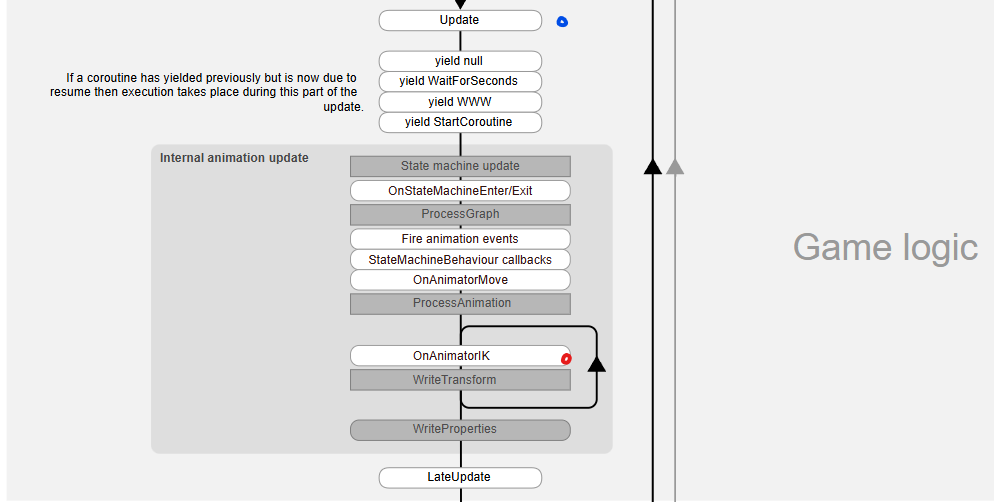
유니티 이벤트 호출 순서를 보면 Update -> ProcessAnimation -> OnAnimationIK -> LateUpdate순서로 호출되는 것을 확인할 수 있다. 따라서 애니메이션이 적용된 후 다시 본의 위치를 재조정하려면 LateUpdate 타이밍에 SolveIK()를 호출하는 것이 적절하다.

public void SolveIK()
{
	...
    var targetPosition = GetPositionRootSpace(_target);
    var targetRotation = GetRotationRootSpace(_target);

    var isReachable = (targetPosition - GetPositionRootSpace(_bones[0].Transform)).sqrMagnitude <
                      _completeLength * _completeLength;
    if (!isReachable)
    {
	    // Just stretch it
	    var direction = (targetPosition - _positions[0]).normalized;
	    for (int i = 1; i < _positions.Length; i++)
		    _positions[i] = _positions[i - 1] + direction * _bonesLength[i - 1];
    }
    else
    {
	    for (var i = 0; i < _positions.Length - 1; i++)
		    _positions[i + 1] = Vector3.Lerp(_positions[i + 1], _positions[i] + _startDirectionSucc[i], SNAP_BACK_STRENGTH);

        for (var iteration = 0; iteration < ITERATIONS; iteration++)
        {
            // Back
            for (var i = _positions.Length - 1; i > 0; i--)
            {
                if (i == _positions.Length - 1)
                    _positions[i] = targetPosition;
                else
                    _positions[i] = _positions[i + 1] + (_positions[i] - _positions[i + 1]).normalized * _bonesLength[i];
            }

            // Forward
            for (var i = 1; i < _positions.Length; i++)
                _positions[i] = _positions[i - 1] + (_positions[i] - _positions[i - 1]).normalized * _bonesLength[i - 1];

            // Close enough
            if ((_positions[^1] - targetPosition).sqrMagnitude < DELTA * DELTA)
                break;
        }
    }

    // Move towards pole
    ...

    // Set position & rotation
    ...
}

이제 실질적으로 IK를 계산하는 부분의 코드를 살펴보자. 닿지 못하는 경우 stretch되는 부분과 Back/Forward가 계산되고 반복되는 과정이 위에 적힌 수식 그대로 구현되었음을 확인할 수 있다. Backword과정에서 End-Effector를 target으로 이동시키고, 루트를 제외한 모든 본들을 조정시킨 후 기존의 루트본에서 다시 Forward를 계산해주고 있다.

// move towards pole
var polePosition = GetPositionRootSpace(Pole);
for (int i = 1; i < Positions.Length - 1; i++)
{
    var plane = new Plane(Positions[i + 1] - Positions[i - 1], Positions[i - 1]);
    var projectedPole = plane.ClosestPointOnPlane(polePosition);
    var projectedBone = plane.ClosestPointOnPlane(Positions[i]);
    var angle = Vector3.SignedAngle(projectedBone - Positions[i - 1], projectedPole - Positions[i - 1], plane.normal);
    Positions[i] = Quaternion.AngleAxis(angle, plane.normal) * (Positions[i] - Positions[i - 1]) + Positions[i - 1];
}

Pole은 IK문제를 해결할 때 본의 방향을 제어하는데 도움을 준다. 신체적으로 부자연스러운 회전을 방지하거나 비일관적 동작을 막기 위해 사용된다. 아래 움짤은 Unreal Engine에서 비슷한 역할을 하는 Joint Target을 설정하고 있는 것이며, 지정된 위치(녹색 점)방향으로 팔꿈치 방향이 이동하는 것을 확인할 수 있다.

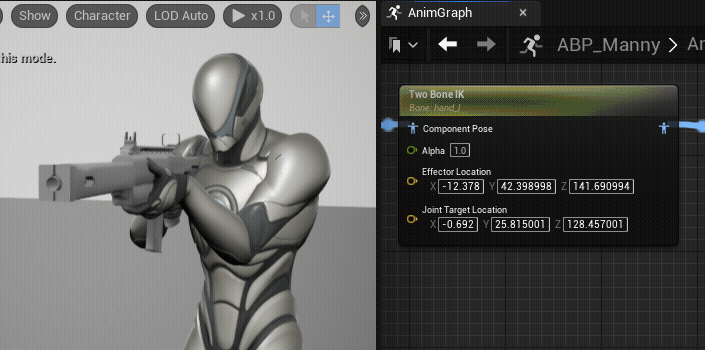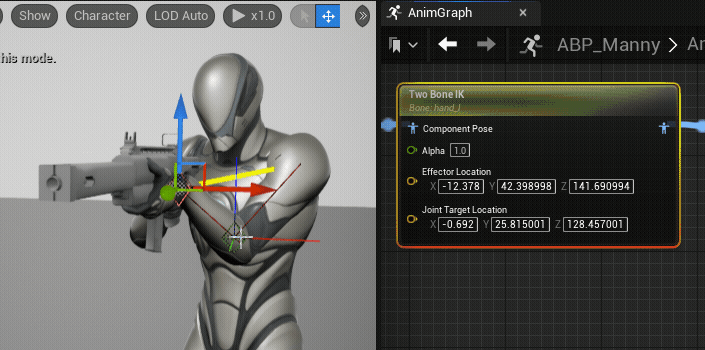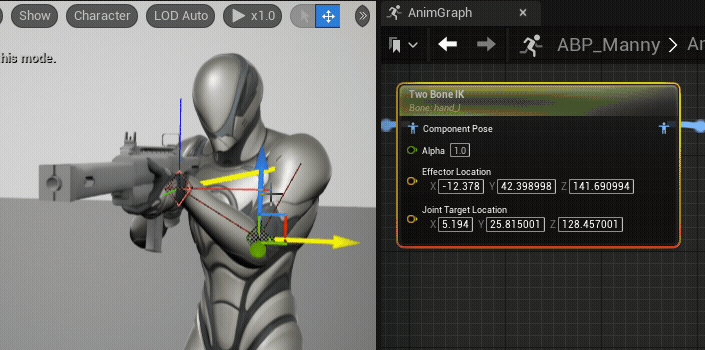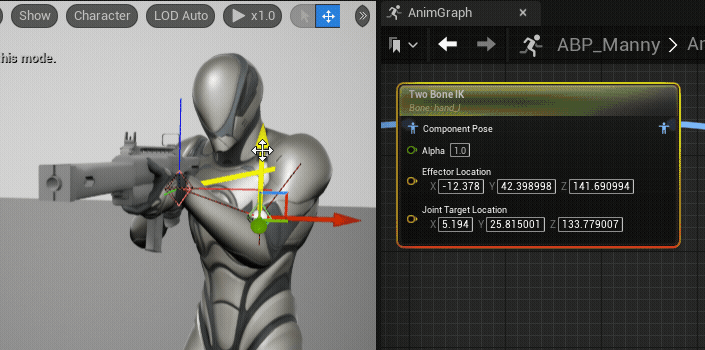
(사진 출처: Unreal Engine - Two Bone IK)

4.2. FootIK

이전 글에서 구현했던 FootIK를 이번에 구현한 FABRIK기반으로 다시 구현해보도록 하겠다. 기본적인 구현방식은 이전과 동일하게 발의 포지션에서 일정 높이 위의 포지션에서 바닥 방향으로 레이를 발사하여 발이 위치할 포지션과 회전값을 지정해 IK를 적용할 것이다.

private FootIkSolverData FeetPositionSolver(Vector3 fromSkyPosition)
{
    if (!Physics.Raycast(fromSkyPosition, Vector3.down, out var feetOutHit,
                         raycastDownDistance + heightFromGroundRaycast, environmentLayer))
    {
        return new FootIkSolverData
        {
            IsDetectGround = false,
            FootPosition   = Vector3.zero,
            FootRotation   = Quaternion.identity
        };
    }

    var feetIkPositions = fromSkyPosition;
    feetIkPositions.y = feetOutHit.point.y + pelvisOffset;
    var feetIkRotations = Quaternion.FromToRotation(Vector3.up, feetOutHit.normal) * transform.rotation;

    return new FootIkSolverData
    {
        IsDetectGround = true,
        FootPosition   = feetIkPositions,
        FootRotation   = feetIkRotations
    };
}

타겟으로 삼을 FootPosition과 FootRotation을 적용하는 부분은 기존 코드와 같다. 이제 여기서 얻은 SolverData를 적용하는 부분도 사실상 이전과 같다. 그저 Unity Animator를 통해 IK포지션을 지정해주던 부분을 위에서 작성한 Fabrik 객체에 넘겨주면 된다.

private void MoveFeetToIkPoint(AvatarIKGoal foot, FootIkSolverData solverData, ref float lastFootPositionY)
{
    if (!solverData.IsDetectGround) return;
    var positionIkHolder = solverData.FootPosition;
    var rotationIkHolder = solverData.FootRotation;
    var targetBone       = foot == AvatarIKGoal.RightFoot ? HumanBodyBones.RightFoot : HumanBodyBones.LeftFoot;
    var targetIkPosition = ObjAnimator.GetBoneTransform(targetBone).position;

    targetIkPosition = transform.InverseTransformPoint(targetIkPosition);
    positionIkHolder = transform.InverseTransformPoint(positionIkHolder);

    var yVariable = Mathf.Lerp(lastFootPositionY, positionIkHolder.y, feetToIkPositionSpeed);
    targetIkPosition.y += yVariable;
    lastFootPositionY  =  yVariable;

    targetIkPosition = transform.TransformPoint(targetIkPosition);

    _fabrik.SetTarget(foot, targetIkPosition, rotationIkHolder);
}

이렇게만 해서 IK를 적용하면 아래 다리 보정 전의 영상처럼 IK가 적용되긴 하는거 같은데 바들바들 떨리면서 이동하는 것을 볼 수 있다. 이건 위에서 언급한 Pole이 셋팅되지 않았기 때문이다. 이후 Pole을 재설정한 이후 정상적으로 걷는 것을 확인할 수 있다. 현재 모델에서 무릎의 Pole은 모델의 정면, Foward방향 벡터에 위치하도록 설정하였다.

영상 마지막쯤에 보면 지형물 위에 올라가 있을 때 살짝 떠있는거처럼 보이는 것을 볼 수 있다. 이는 현재 구현된 IK에는 본이 늘어나지 않도록 구현되었기 때문에 원래 본들을 쭉 핀 거리보다 위치해야할 발의 포지션이 멀리 떨어져 있는 경우 이러한 상황이 나올 수 있다. 이런 경우 발이 땅에 닿을 수 있게 골반을 추가적으로 보정해주면 아래 스크린샷과 같이 발이 땅에 닿는 것을 확인할 수 있다.

(그림자때문에 이것도 살짝 떠있는거처럼 보이긴 하는데.. 위 영상보다 무릎을 더 많이 굽히는건 확인할 수 있다)

4.3. HandIK

위 로직이 HandIK에서도 잘 적용되는지 테스트하기 위해 간단한 HandIK예제를 만들어보자. 현재 테스트중인 게임의 캐릭터에는 펀치로 적을 공격하는 Muscle Cat캐릭터가 있는데, 해당 캐릭터의 주먹이 특정 타겟을 공격하도록 애니메이션을 보정해보려고 한다.

다양한 펀치 애니메이션에 대해서 후보정을 수정하기는 까다롭기 때문에, 애니메이터에서 사용하는 모든 펀치 애니메이션을 RightHook anim 데이터를 이용하도록 수정하고, 해당 애니메이션에서 IK를 이용한 후보정을 진행해보도록 하겠다.

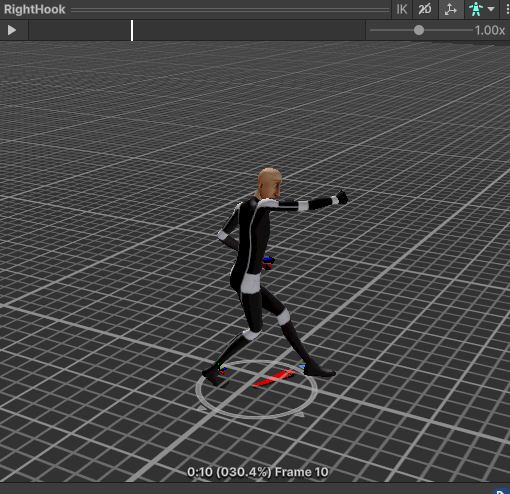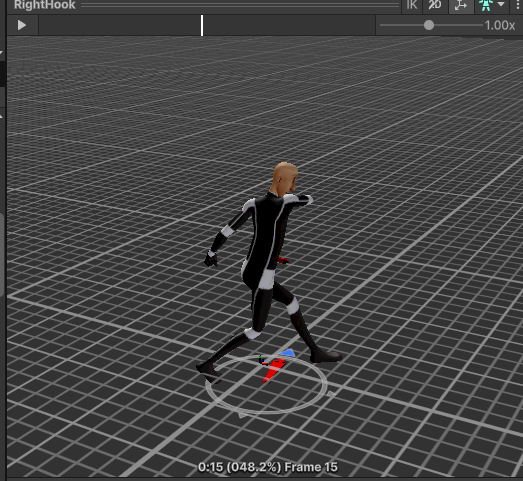
위 스크린샷은 RightHook 애니메이션에서 주먹을 뻗는 부분(10 프레임)과 주먹을 거두는 부분(15프레임)을 캡쳐한 것이다. 해당 프레임을 기준으로 주먹을 뻗는 부분에서 정해진 타겟을 가격하도록 애니메이션을 수정한 후 주먹을 거두는 애니메이션 쯤 원래 애니메이션으로 돌아오도록 애니메이션을 보정해보겠다.

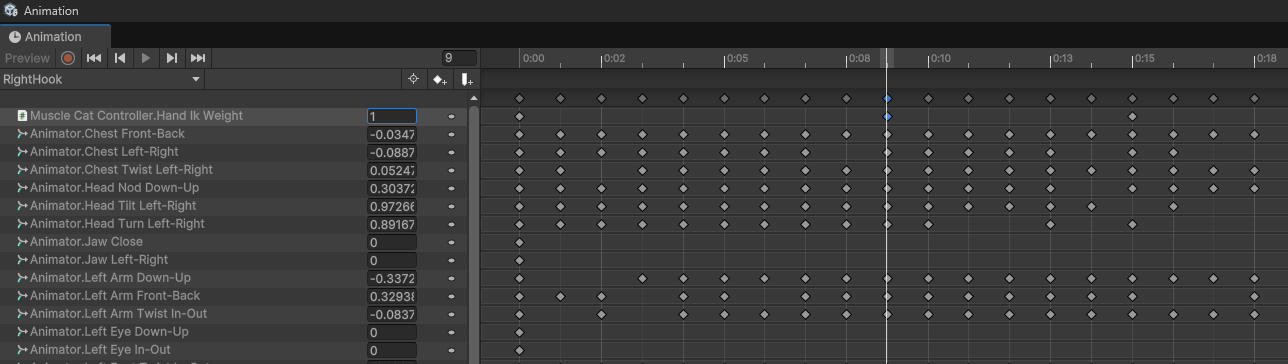
사용할 캐릭터 제어 스크립트에 HandIkWeight라는 필드를 추가 후, RightHook anim 데이터에서 10프레임에 해당 값을 1, 0과 15프레임에 해당 값을 0으로 셋팅하도록 하였다. 지정된 프레임 사이 값은 애니메이터에서 기본적으로 보간해주는 값으로 설정되어있다.

        [SerializeField] private Transform rightHandTarget;

        protected override void LateUpdate()
        {
            base.LateUpdate();

            if (rightHandTarget && HandIkWeight > 0.01f)
            {
                var rightHand = ObjAnimator.GetBoneTransform(HumanBodyBones.RightHand);
                var targetPosition = Vector3.Lerp(rightHand.position, rightHandTarget.position, HandIkWeight);
                var targetRotation = Quaternion.Lerp(rightHand.rotation, rightHandTarget.rotation, HandIkWeight);
                Fabrik.SetTarget(AvatarIKGoal.RightHand, targetPosition, targetRotation);
            }
        }

샘플 코드는 매우 간단하게 작성되었다. 애니메이션으로 지정되는 값인 HandIkWeight가 0.01이상이며 rightHandTarget이 있는 경우 주먹의 Transform값과 Target의 Transform값을 보간하여 애니메이션을 보정하도록 셋팅하였다.

HandIK를 적용 후, 주먹을 뻗을 때 지정된 타겟 포지션으로 주먹이 나가는 것을 확인할 수 있다.

하지만 어색한 점을 확인할 수 있는데 본의 회전 값이 매우 어색한 포인트들을 발견할 수 있다. FABRIK의 기본 구현에서 신체의 각도 제한을 고려하지 않기 때문에 물리적으로 불가능한 애니메이션이 수행되는 경우가 있다. 이를 방지하기 위해서는 다음과 같은 방법들이 있다.

• 컨텐츠 로직: IK 후보정을 수행하는 조건에 시야에 따라 일정 각도 안에 있는 오브젝트에 대해서만 IK Target으로 판정을 해주는 로직을 추가하는 방법
• IK 로직: 회전값이 없는 IK Target 설정 메서드 추가 또는 본의 자유도를 제한하거나 일정 범위에서만 회전이 가능하도록 변화값의 제한 추가

IK 로직의 개선에 대한 내용은 아래 개선사항에서 조금 더 자세히 다뤄보도록 하겠다.

5. 개선사항

---

위에서 언급했듯이, FABRIK는 각도 제한을 고려하지 않는다. 따라서 자연스러운 신체 움직임을 위해서는 추가적인 보정이 필요한데, 위 걷기 애니메이션에서는 단순히 무릎 앞쪽으로 Pole을 지정해주는 것 만으로도 자연스럽게 보정이 되었다. 하지만 모든 상황에서 Pole을 지정해준 것 만으로 자연스러운 애니메이션이 가능하지는 않을 것이다. 조인트간 자유도 지정, 회전 각도 제한 등 물리적으로 가능한 애니메이션만 수행하도록 보정이 더 필요하다.

Humanoid Model에서 쓰는 Joint들은 아래와 같은 자유도를 가진다.

• suture joint model (1 DoF) : 절대 열리면 안되는 fixed joint. 움직이더라도 매우 제한적으로 움직일 것. 두개골과 같은 곳에 쓰임.
• hinge joint model (1 DoF) : 가장 단순한 형태의 joint. 팔꿈치, 무릎, 손가락/발가락 등에 사용됨. 한 방향으로만 rotation이 이루어짐.
• gliding joint model (2 DoF) : 손목, 발목과 같이 보다 넓게 회전이 가능한 joint
• saddle joint model (2 DoF) : hinge나 gliding보다 자유롭게 움직일 수 있는 joint. 두 방향으로 움직일 수 있음.
• pivot joint model (2 DoF) : 목과 같은 곳에 쓰이는 joint. 좌우로 돌릴 수 있음.
• ball and socket joint model (3 DoF) : 인체에서 가장 유동적인 형태의 joint. 타원형 joint임.

(내용 출처: GE2022-1.-Introduction-to-Inverse-Kinematics)

또한 언리얼 엔진의 Two Bone IK에서 설정 가능한 파라메터들을 보면 어떠한 보정을 해줄 수 있을지 힌트를 얻을 수 있다. Stretch 관련된 셋팅 값들이나 Twist, Joint Target에 대한 설명을 보면 해당 프로퍼티들이 IK를 어떻게 제어하는지 알 수 있다.

자연스럽게 걸어보아요

참고

---

Overview of Jacobian IK
[GE] 1. Introduction to Inverse Kinematics 시리즈