[Paper Review] Resurrecting Recurrent Neural Networks for Long Sequences

서쿠·2024년 9월 23일

논문 "Resurrecting Recurrent Neural Networks for Long Sequences"는 25 Apr 2023에 publish되었으며, ICML 2023 OralPoster에 발표된 논문입니다.

해당 논문은 "Recurrent Neural Networks (RNN)의 성능을 복원하여 긴 시퀀스에서의 효율적인 학습과 추론"을 다루고 있습니다. 본 paper-review에서는 각 챕터별로 주요 내용을 정리해보았습니다.

링크 : https://proceedings.mlr.press/v202/orvieto23a/orvieto23a.pdf

1. Introduction

논문의 서론은 Recurrent Neural Networks(RNNs)가 긴 시퀀스를 처리할 때 겪는 문제점과 그에 대한 해결책을 제시하며, 최근의 연구 동향을 설명하고 있습니다.

1.1. RNN의 중요성과 한계

RNN은 순차적 데이터(시계열, 자연어 등)를 처리하는 데 오랜 시간 동안 중요한 역할을 해왔습니다. RNN은 데이터를 순차적으로 처리하기 때문에 시퀀스 간의 의존성을 학습할 수 있는 능력이 뛰어납니다. 그러나 실전에서 RNN을 학습시키는 것은 매우 어려운 일입니다.

주된 이유는 기울기 소실(vanishing gradient)과 기울기 폭발(exploding gradient) 문제 때문입니다. 이는 RNN이 긴 시퀀스를 학습할 때, 초반에 입력된 정보가 네트워크를 통해 전달되면서 점점 약해지거나, 너무 강해져서 학습이 불가능해지는 현상을 의미합니다.

기울기 소실 문제는 네트워크의 초기 층이나 깊은 층에서 기울기가 매우 작아져서, 가중치 업데이트가 이루어지지 않거나 매우 느리게 이루어지는 현상입니다.
- 비선형 활성화 함수: 입력값이 비선형 함수의 극한에 도달할 때 해당 함수의 기울기가 0이 되기 때문에, 그 이후의 층으로 전달되는 기울기가 모두 0에 가까워진다.
- 층이 깊어질수록: RNN은 시간에 따라 연속적으로 여러 층을 쌓아 나가기 때문에, 각 단계에서 신호가 전파될 때 기울기가 곱해져서 감소하게 된다.
기울기 폭발 문제는 기울기가 너무 커져서 가중치 업데이트가 극심해지는 현상입니다. 이로 인해 모델이 학습 중에 발산하게 될 수 있습니다.
- 기울기 조합: RNN 모델에서 여러 층의 가중치가 곱해지면서 기울기가 지수적으로 증가할 수 있습니다.
- 부적절한 초기화: 가중치를 잘못 초기화하면 훈련 중에 기울기가 큰 값을 가지게 되면서, 업데이트도 비정상적으로 커지게 됩니다.

이 문제를 해결하기 위해 몇 가지 기술들이 개발되었습니다. 예를 들어, LSTM(Long Short-Term Memory)과 GRU(Gated Recurrent Units) 같은 게이트 메커니즘을 사용하는 모델들이 있습니다. 이들은 RNN의 한계를 극복하려고 고안된 방식이지만, 여전히 학습 과정에서 속도가 느리고, 대규모 데이터에서 확장성(scalability)이 부족하다는 문제가 남아 있습니다.

1.2. Transformer 모델의 대두

최근에는 Transformer 모델이 등장하면서 순차적 데이터 처리에서 큰 성공을 거두었습니다.

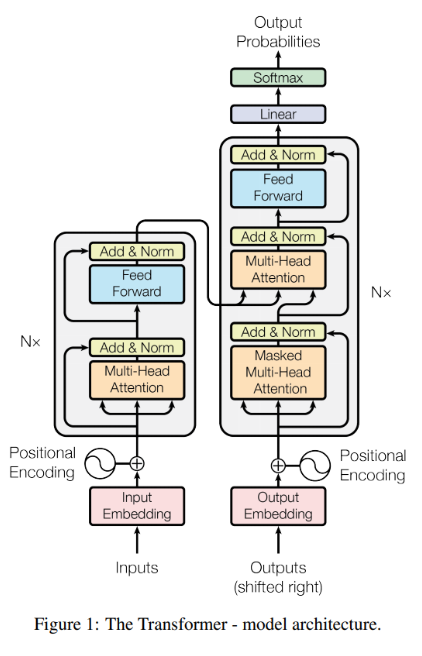
Transformer는 주의(attention) 메커니즘을 사용하여 시퀀스의 각 요소 간의 상호작용을 직접 모델링합니다. 이로 인해 RNN과 달리 기울기 소실 문제가 발생하지 않으며, 병렬화가 가능해 대규모 데이터 학습에 유리합니다. 이러한 장점 덕분에 자연어 처리, 이미지 처리 등 다양한 분야에서 탁월한 성능을 발휘하고 있습니다.

그러나 Transformer의 가장 큰 문제는 메모리 및 계산 비용이 시퀀스 길이에 따라 Quadratic하게 증가한다는 점입니다. 시퀀스 길이가 길어질수록 메모리와 연산 비용이 급격히 증가하여, 긴 시퀀스를 다루는 데 효율적이지 않습니다.

이에 반해, RNN은 시퀀스 길이에 비례하는 Linear한 Cost만을 요구하므로, 긴 시퀀스에서 추론할 때 여전히 더 빠릅니다.

1.3. 상태공간모델(SSM)의 등장

이러한 Transformer의 문제점을 해결하기 위해 Gu et al. (2021)이 제안한 State Space Model(SSM)을 활용한 S4(Structured State Space Model)모델이 주목받기 시작했습니다.

S4 모델은 Long Range Arena(LRA)라는 긴 시퀀스를 다루는 벤치마크에서 뛰어난 성능을 보여주며, 특히 긴 시퀀스를 효율적으로 처리할 수 있는 능력을 가지고 있습니다. SSM은 시퀀스 간의 상호작용을 순차적으로 처리하면서도 병렬 처리가 가능하고, 추론 속도도 빠릅니다. (다음 paper-review에서 정리해볼게요!)

이는 RNN과 유사한 방식으로 작동하면서도, 학습 속도와 성능 면에서 Transformer보다 효율적입니다.

1.4. 연구 목표와 핵심 기여

서론의 마지막 부분에서는 이 논문의 연구 목표를 제시합니다. RNN과 SSM의 성능 차이를 분석하고, RNN을 개선하여 SSM 수준의 성능을 복원하는 방법을 탐구하는 것이 이 논문의 주된 목표입니다. 이를 위해, RNN의 구조를 세밀하게 조정하는 여러 가지 방법을 제안합니다. 이 방법들을 통해 RNN도 SSM과 동일한 성능을 발휘할 수 있음을 보여주고, 이러한 수정이 RNN의 학습 속도에도 긍정적인 영향을 미친다는 점을 강조합니다.

논문에서는 아래와 같은 화두를 던지며 해당 질문에 긍정적(positive)라고 이야기합니다.

연구자들은 deepRNN을 사용하여 깊은 연속 시간 상태 공간 모델(SSM)의 성능과 효율성을 일치시킬 수 있음을 주장합니다. 이를 달성하기 위해 논문에서 제시한 몇 가지 주요 접근 방식을 설명하겠습니다.

Linear Recurrences (선형 재귀): 기존의 tanh 또는 ReLU 활성화를 사용하는 RNN 계층 대신 비선형성을 제거하고 선형 재귀(선형적으로 반복되는 구조)를 사용하여 성능이 크게 향상된다는 것을 발견했습니다. 여기서 선형적으로 반복되는 구조란, 예를 들어 tanh나 ReLU와 같은 활성화 함수를 사용하지 않고 단순히 행렬 곱셈과 덧셈만을 통해 상태를 갱신하는 방식입니다. 선형 재귀를 사용하면 gradient의 소실 또는 폭발을 직접 제어할 수 있으며, 병렬화된 훈련이 가능해집니다.
Complex Diagonal Recurrent Matrices (복소수 대각 재귀 행렬): 밀집 선형 RNN 계층을 복소수 대각 형태로 재구성하는 것으로도 성능이 향상됩니다. 밀집 선형 RNN 레이어는 네트워크의 표현력을 손상시키지 않으면서 복잡한 대각 형태로 재매개변수화할 수 있습니다. 이를 통해 초기화에서의 특성도 유지됩니다. 대각 행렬은 반복적인 과정을 병렬로 풀 수 있게 해주어 훈련 속도를 크게 향상시킵니다.
- 대각행렬들은 곱셈 연산에서 결합법칙을 만족하기 때문에, 각 연산을 병렬화할 수 있습니다. 이를 통해 RNN과 같은 모델의 훈련 속도를 크게 개선할 수 있습니다. (Martin & Cundy, 2017).
- (참고) 대각 행렬 곱셈의 특성 : 대각 행렬은 비대각선 요소가 모두 0이기 때문에, 곱셈 연산이 각 대각선 요소끼리만 이루어집니다. 즉, 각각의 요소가 독립적이기 때문에, 병렬로 연산이 가능해집니다.
- (참고) 결합법칙 : 대각 행렬의 곱셈은 결합법칙을 만족합니다. 즉, A×(B×C)=(A×B)×C와 같은 방식으로 연산 순서에 상관없이 동일한 결과를 얻을 수 있습니다. 이는 병렬 처리에 매우 유리한 특성입니다.
Stable Exponential Parameterization (안정적인 지수 파라미터화): 대각 재귀 행렬에 대한 지수 파라미터화를 사용하면 안정성을 보장할 수 있으며, 이로 인해 초기화 분포를 조정하여 장기적인 추론 성능을 향상시킬 수 있습니다. 초기화 시 고유값 분포가 장기 추론을 캡처하는 데 중요한 역할을 한다고 강조합니다.
Normalization (정규화): 훈련 과정에서의 숨겨진 활성화를 정규화하는 것이 매우 중요하다고 언급했습니다. 이를 통해 RNN이 LRA(Long Range Arena) 벤치마크의 모든 Task에서 SSM의 성능과 준하는 성능을 낼 수 있었습니다.

본 논문은 RNN의 성능을 되살리기 위해 Linear Recurrent Unit(LRU)라는 새로운 블록을 제안하며, LRU가 SSM과 유사한 성능과 효율성을 갖출 수 있음을 실험적으로 입증합니다. 제안된 LRU는 Long Range Arena(LRA) 벤치마크에서 SSM과 동등한 성능을 보이며, 병렬 학습 속도도 일치합니다.

2. Preliminaries

이 장에서는 전통적인 RNN과 최근의 S4와 같은 deepSSM의 주요 차이점을 설명합니다.

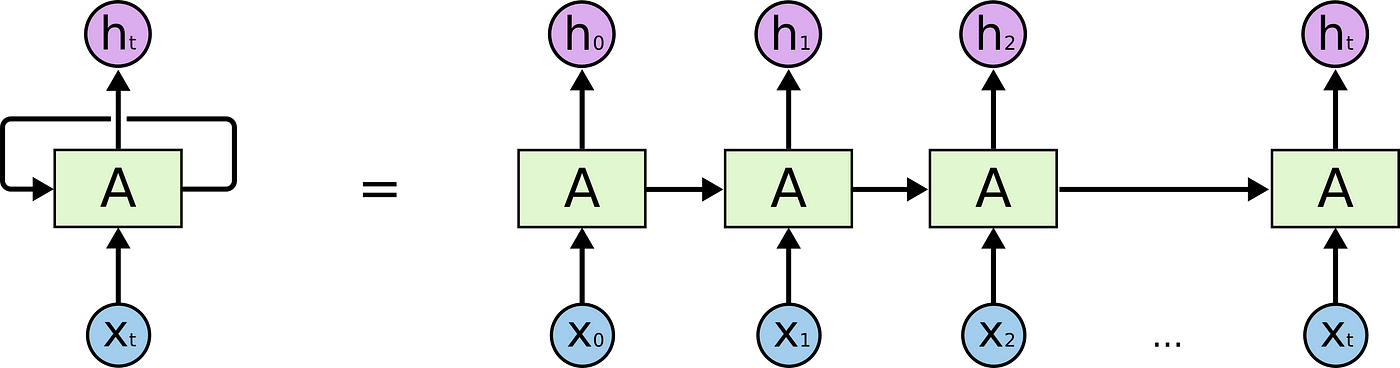
RNN (Recurrent Neural Network)

RNN은 순차적으로 데이터를 처리하는 신경망 구조입니다. 여기서 중요한 것은 이전 단계의 상태 정보가 현재 상태를 계산하는 데 사용된다는 점입니다.

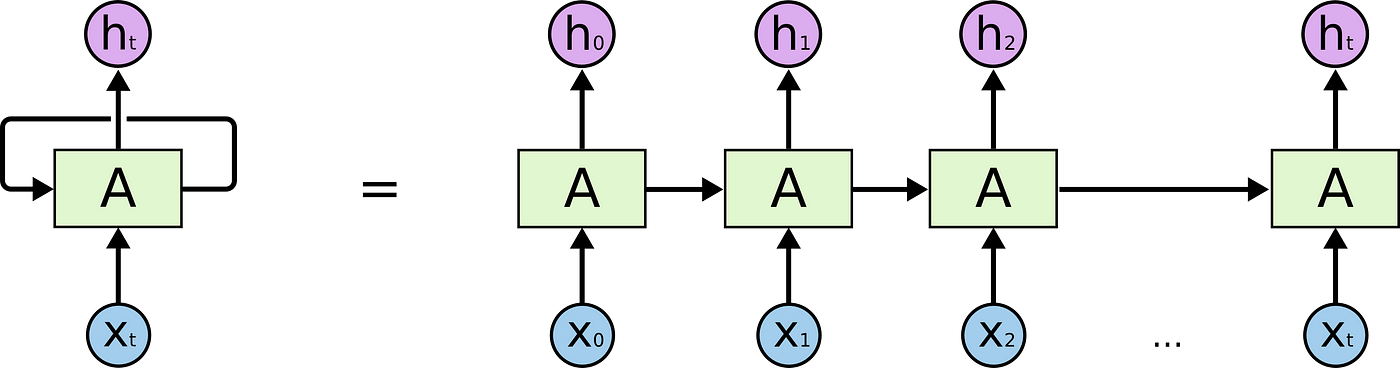
이는 다음 수식으로 표현됩니다:

x_k = \sigma(Ax_{k-1} + Bu_k), \quad y_k = Cx_k + D u_k

여기서:

$A$ , $B$ , $C$ , $D$ 는 학습 가능한 매개변수입니다.
$\sigma$ 는 비선형 활성화 함수로 보통 tanh나 sigmoid가 사용됩니다. 만약 $\sigma$ 가 항등 함수(identity function)라면 RNN은 선형 RNN으로 간주됩니다.
$x_k$ 는 $k$ 번째 시점에서의 히든 상태(hidden state)이고, $y_k$ 는 출력입니다.

일반적으로 tanh나 ReLU 같은 비선형 활성화 함수를 사용하여 상태 전이를 이루며, 매번 이전 상태에서 새로운 입력을 받아 반복적으로 상태를 업데이트합니다.

하지만 RNN은 비선형성을 갖고 있어 학습 과정에서 기울기 소실 문제로 인해 학습이 어려울 수 있습니다.

SSM (State Space Model)

SSM은 연속 시간 시스템을 기반으로 한 모델입니다. 연속적인 시간 축에서 상태 변화를 모델링하고, 이를 이산화하여 시퀀스 데이터를 처리할 수 있습니다.

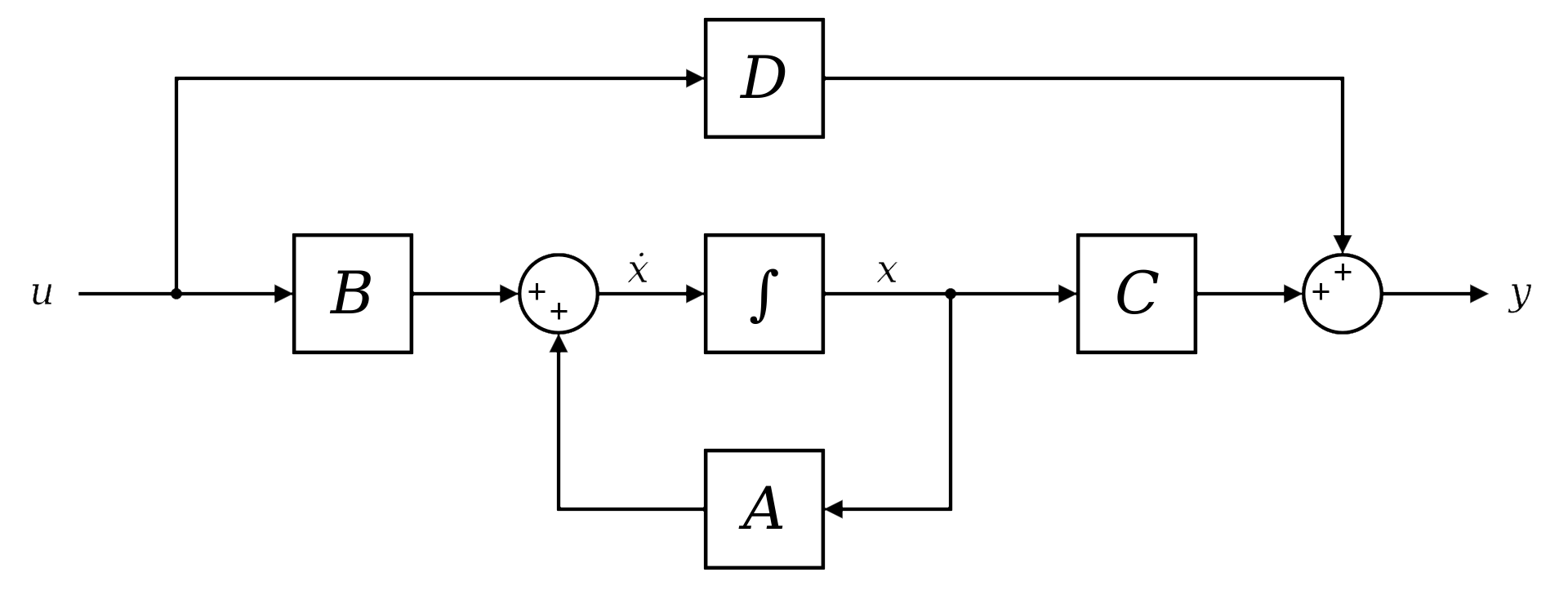
이는 수학적으로는 다음과 같이 설명됩니다:

\frac{d}{dt}x_{ct}(t) = Ã x_{ct}(t) + B̃ u_{ct}(t)

y_{ct}(t) = \mathcal{R}(C̃ x_{ct}(t)) + D̃ u_{ct}(t)

이 모델에서 입력 신호 $u_{ct}$ 는 연속 시간에서 샘플링된 시그널로 간주됩니다. 이 상태 공간 모델은 긴 시퀀스에서도 안정적인 계산을 보장하며, 특히 복잡한 상호작용을 효율적으로 처리할 수 있습니다.

S4 (Structured State Space Sequence Model)

S4는 위의 SSM을 기반으로 설계된 딥러닝 모델로, 긴 시퀀스 모델링에서 뛰어난 성능을 발휘합니다. 이 모델은 복소수 행렬을 사용하여 RNN보다 더 효율적으로 학습할 수 있으며, 병렬화가 가능하다는 장점이 있습니다.

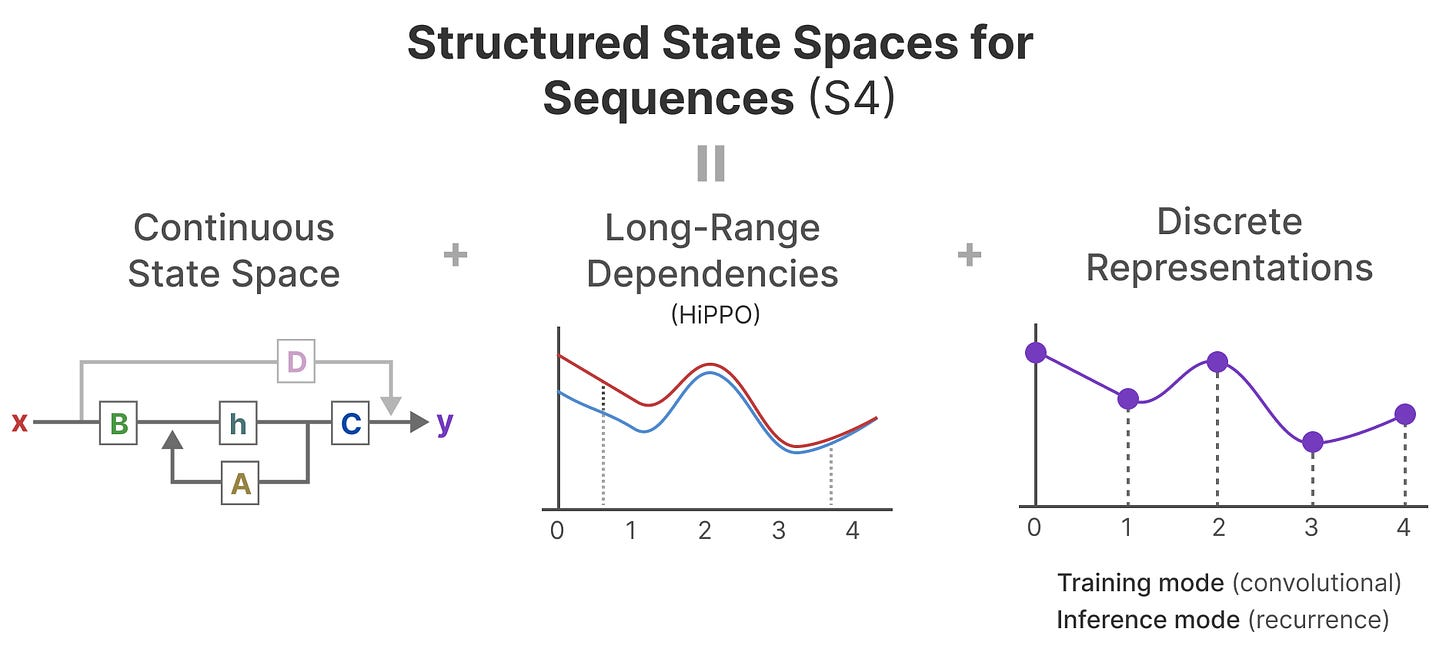
이미지 출처 : A Visual Guide to Mamba and State Space Models (링크)

S4는 상태 공간 모델을 기반으로 한 매우 효율적인 모델입니다. S4는 복잡한 긴 시퀀스를 처리할 수 있는 능력으로 주목받고 있으며, 다음과 같은 특징을 가지고 있습니다:

연속 시간 기반의 상태 공간 모델: S4는 상태 공간 모델을 사용하여 연속적인 신호를 처리하고 이를 이산 시간으로 변환합니다.
병렬 처리 가능: S4는 선형 시스템을 기반으로 하여 RNN과 달리 학습 과정에서 병렬 처리가 가능합니다.
HiPPO 이론을 기반으로 한 초기화: S4는 HiPPO 이론을 바탕으로 복잡한 초기화 방법을 사용하여 모델의 성능을 극대화합니다. 이 초기화 과정은 SSM이 긴 시퀀스를 처리할 때 중요한 역할을 합니다.

S4는 RNN과 비교했을 때 긴 시퀀스를 더 효율적으로 처리하며, RNN의 병목 현상(Sequential Processing)을 극복할 수 있는 성능을 보여줍니다.

3. Designing Performant Deep RNNs

이 장에서는 논문에서 제안하는 성능이 뛰어난 깊은 RNN(Deep RNN)을 설계하기 위한 주요 단계를 설명합니다. 연구진은 SSM(상태 공간 모델)의 뛰어난 성능을 재현하고자 RNN의 구조적 변형을 통해 SSM과 비슷한 성능을 달성할 수 있음을 보여줍니다.

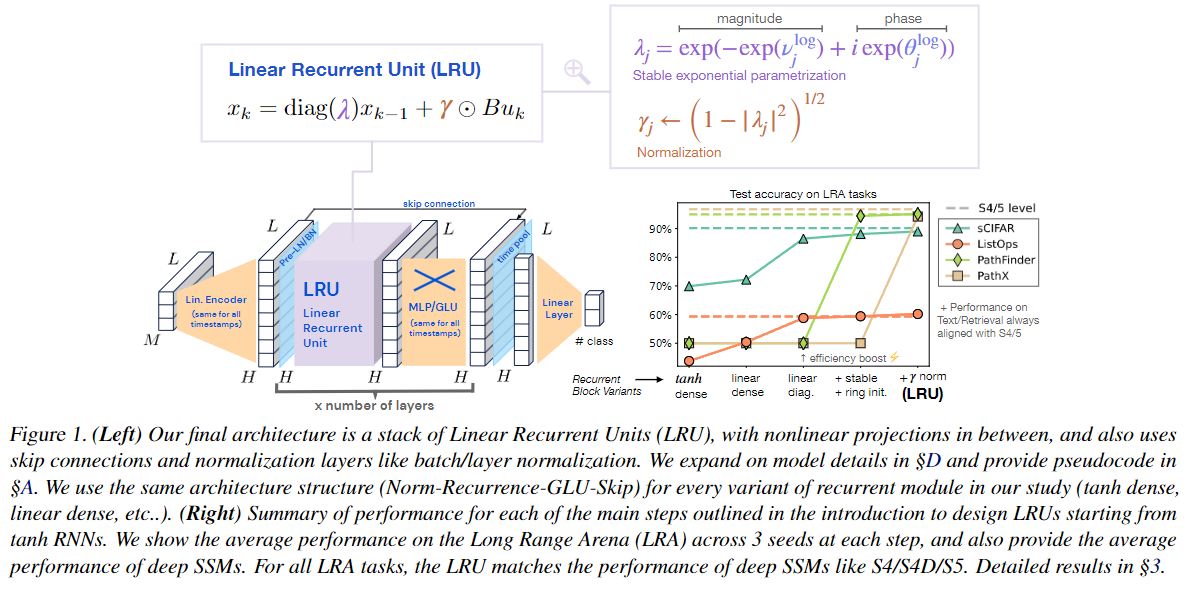
먼저 위에서 보여드린 그림을 탐구해봅시다.

(Left) Deep Linear Recurrent Unit (LRU) Architecture

왼쪽 그림은 LRU 의 세부 구조를 보여줍니다.
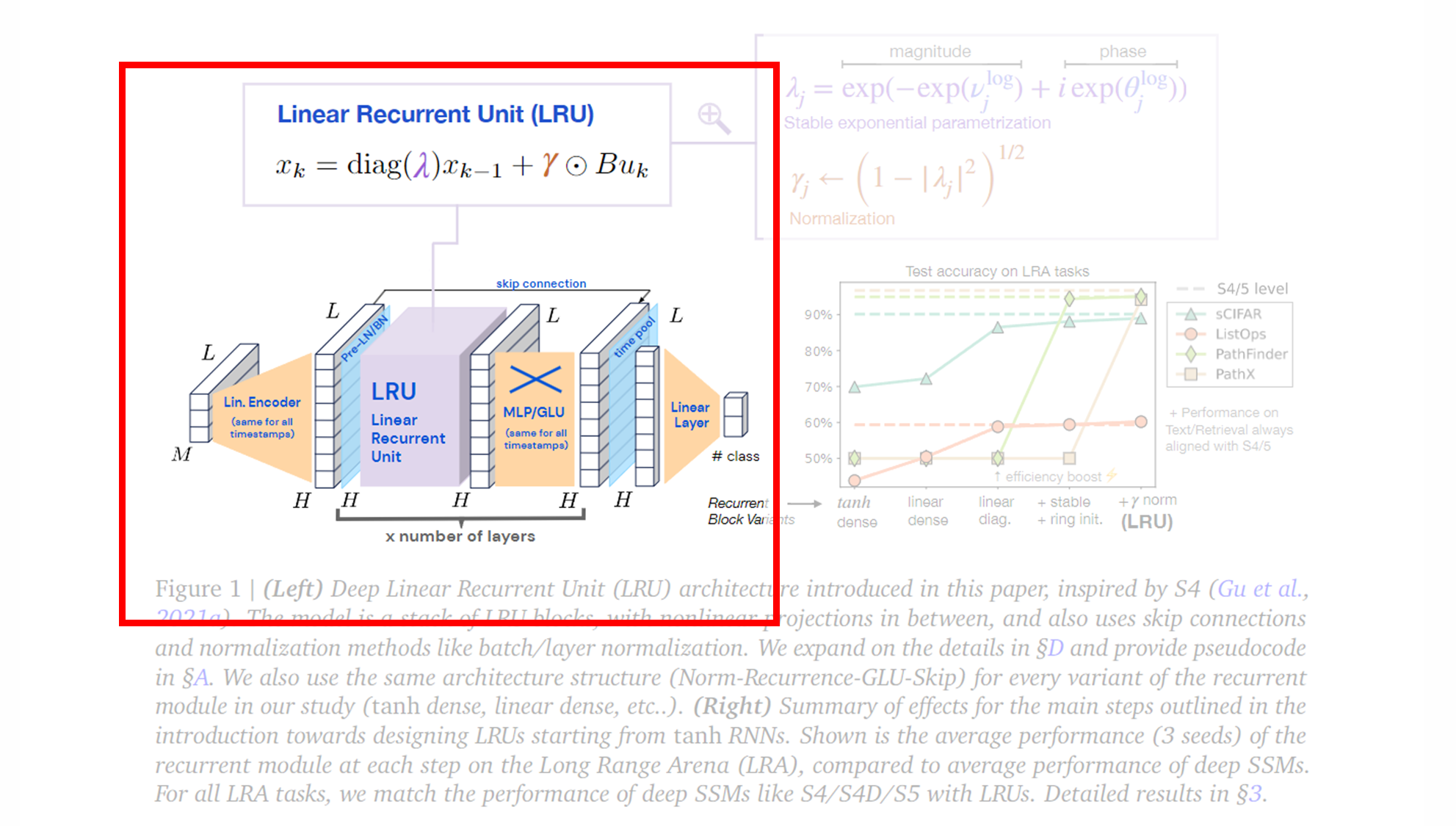
- Linear Encoder (선형 인코더) :
  - 입력 시퀀스를 선형 인코더에 통과시킵니다.
    - 이 인코더는 모든 타임스텝에 대해 동일하게 적용되며, 입력 데이터를 적절한 형태로 변환합니다.
  - 차원 축소 또는 변환을 통해 모델이 처리할 수 있는 형태로 데이터를 전달합니다.
- Linear Recurrent Unit (LRU) :
  - LRU 블록 은 여러 개의 층으로 쌓인 구조를 가지며, 각 층 사이에는 MLP/GLU 블록이 삽입되어 비선형성을 추가합니다.
    - 여기서 MLP는 Multi-Layer Perceptron 을 의미하고, GLU는 Gated Linear Unit 을 의미합니다.
  - LRU는 RNN의 기본적인 순환 신경망 구조를 따르고 있지만, 몇 가지 중요한 변형을 통해 성능을 개선한 버전입니다.
    - 특히, 비선형성을 제거하고, 복소수 대각 행렬을 사용하는 등, RNN의 효율성을 높이기 위한 여러 개선 사항을 포함하고 있습니다.
    - 하지만 순환적인 상태 전이와 시퀀스 처리라는 RNN의 핵심 특성은 유지하고 있기 때문에 LRU도 RNN의 한 형태라고 할 수 있습니다.
  - LRU의 핵심은 선형 반복 을 사용하며, 이를 통해 RNN의 비선형성을 제거하면서도 강력한 성능을 유지할 수 있습니다. 이 구조는 병렬화가 가능하며, 학습 속도를 향상시킵니다.
  - LRU의 반복 수식은 아래와 같습니다:
    
    $x_k = \text{diag}(\lambda) x_{k-1} + \gamma \odot B u_k$
    - $diag(λ)$ : 복소수 대각 행렬로, 이는 상태 전이를 더 효율적으로 계산할 수 있게 해줍니다.
    - $γ$ : 학습 가능한 정규화 파라미터로, 이는 각 시퀀스 타임스텝에서 상태 정보를 조정하는 역할을 합니다.
    - $B u_k$ : 입력 데이터 $u_k$ 에 대해 가중치 $B$ 를 곱하여 다음 상태로 전달합니다.
  - 세부 파라미터를 좀 더 살펴보겠습니다.
  - Normalization (정규화, $\gamma_j$ ) :
    - LRU 내부에서는 Pre-Layer Normalization 또는 Batch Normalization 이 적용되어 긴 시퀀스 학습 중 발생할 수 있는 기울기 소실 문제를 완화합니다.
    - 정규화는 각 층에서 발생하는 은닉 상태의 스케일을 조정하여 학습을 안정화시킵니다.
      $\gamma_j = (1 - |λ_j|^2)^{1/2}$
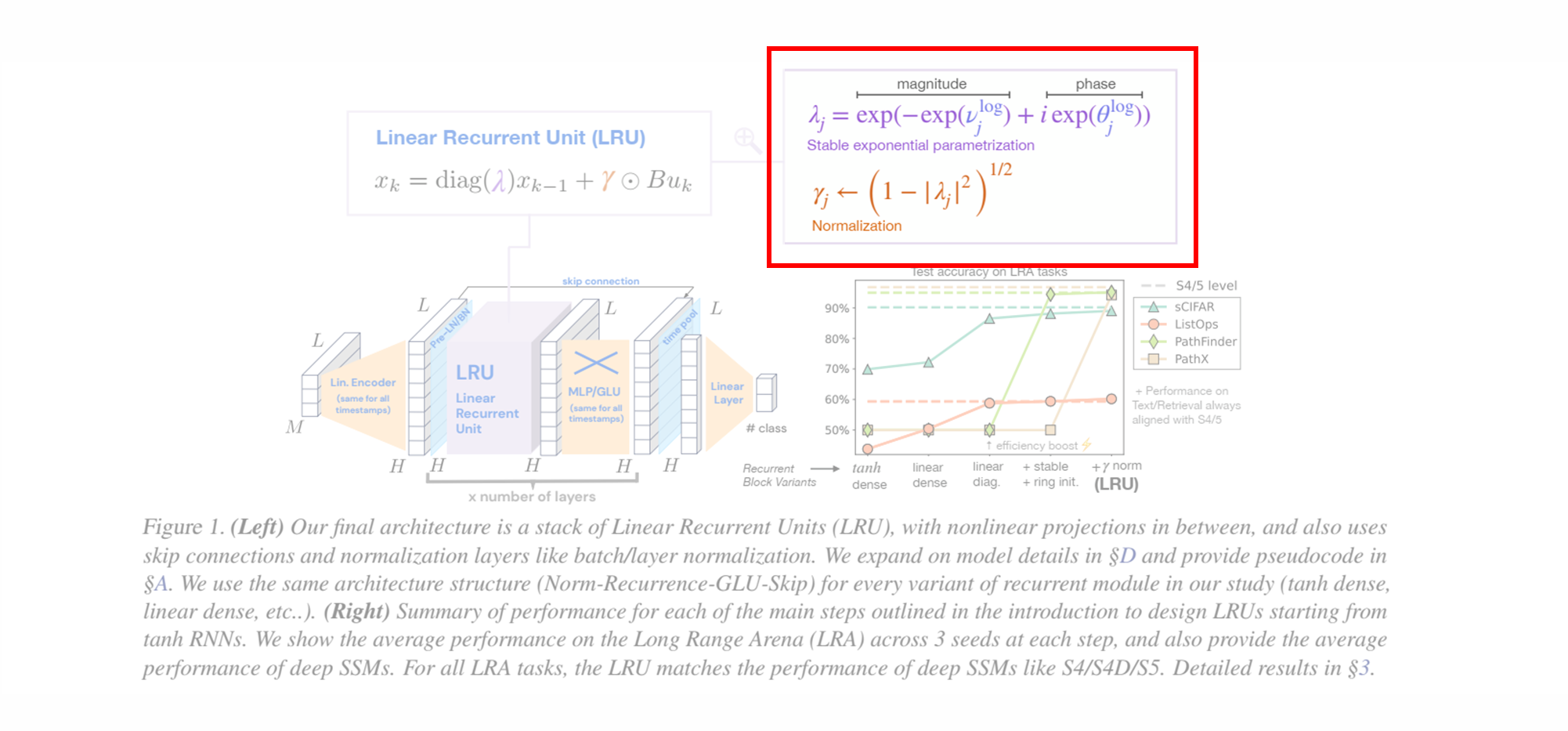
  - Stable Exponential Parameterization (안정적인 지수 매개변수화, $λ_j$ )
    - RNN의 반복 행렬을 매개변수화할 때, 학습 과정에서 안정성을 보장하기 위해 수행됩니다.
    - 이는 모델이 학습하는 동안 기울기 소실(vanishing gradient) 또는 기울기 폭발(exploding gradient)을 방지하여, 특히 긴 시퀀스에서 오버플로우 또는 언더플로우 문제를 해결하는 데 중요한 역할을 합니다.
      
      $λ_j = exp(-exp(ν_j^log) + i exp(θ_j^log))$
      - λ는 복소수 고유값이며, 이는 학습 중에 매개변수화되어 안정성을 보장합니다.
      - 고유값의 크기와 위상을 각각 매개변수화하여 학습 성능을 높입니다.

Skip Connection :
- 각 층 사이에는 Skip Connection 이 포함되어 있습니다. 이는 모델이 깊어질수록 발생할 수 있는 정보 손실을 방지하고, 더 깊은 네트워크에서 효과적인 학습을 가능하게 합니다.
Linear Layer (선형 출력 레이어) :
- 마지막으로, 타임스텝과 관련된 출력을 위해 선형 레이어 가 사용됩니다. 이는 모델의 최종 출력으로 이어지며, 클래스 예측이나 기타 시퀀스 모델링 작업에 사용됩니다.

(Right) Test accuracy on LRA tasks

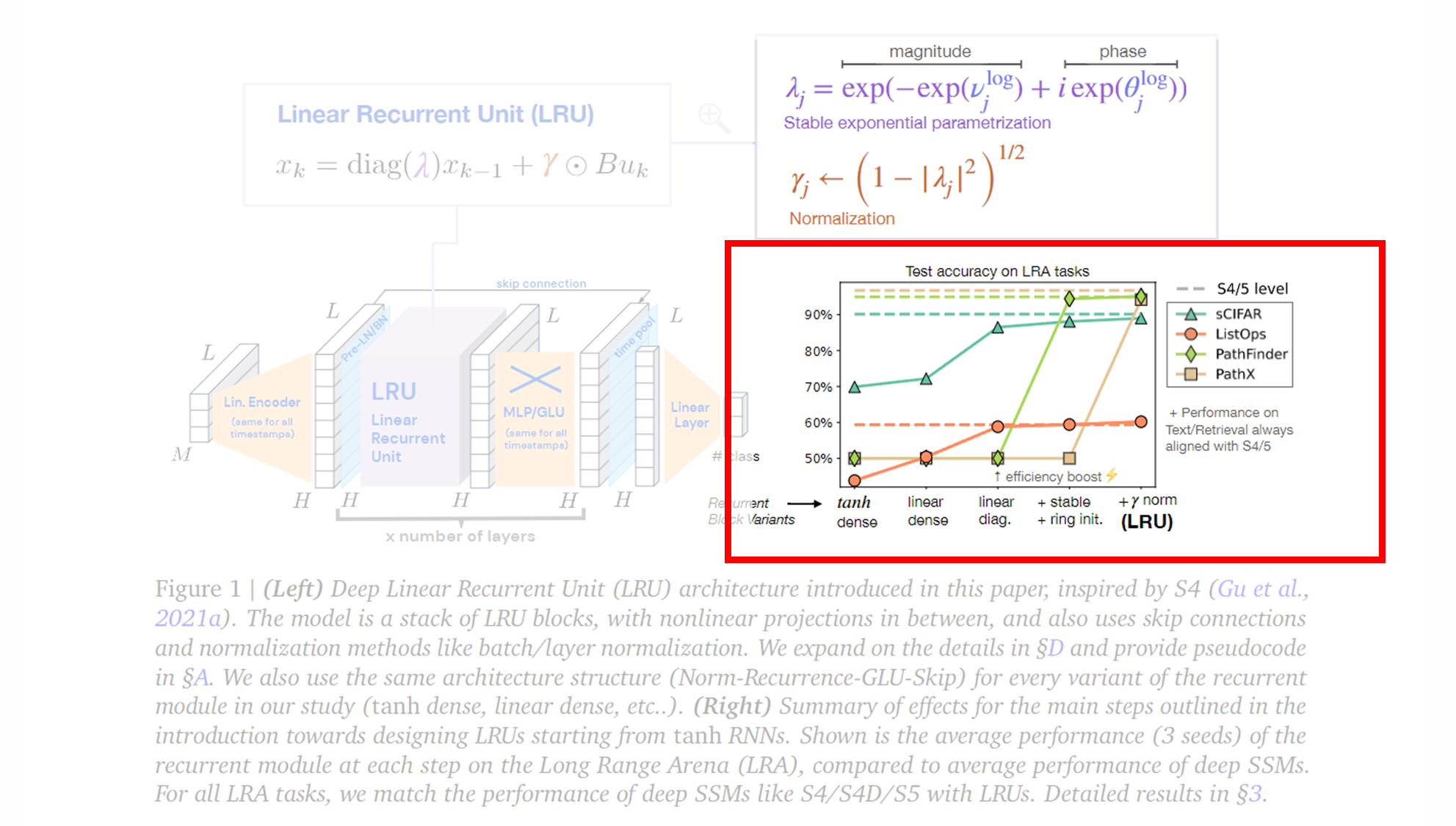
오른쪽 그래프는 Long Range Arena (LRA) 벤치마크에서 수행한 테스트 결과를 시각적으로 보여줍니다. 이 그래프는 RNN 구조에서 tanh 활성화 함수를 사용하는 기본 RNN에서 시작하여, LRU 구조로 변경해가면서 성능이 어떻게 변화하는지를 나타냅니다.

Recurrent Block Variants (RNN 블록 변형) :
- X축은 반복 모듈의 여러 변형을 나타냅니다. 초기 tanh 활성화 RNN에서 시작하여, 선형 활성화 , 대각선화(복소수 대각 행렬) , 안정적인 지수 매개변수화 , 그리고 최종적으로 γ 정규화 를 포함하는 LRU까지 발전합니다.
- 각 단계에서 RNN이 어떻게 개선되고 있는지 확인할 수 있습니다.
Efficiency Boost (효율성 향상) :
- 그래프에서 주목할 점은 선형 대각 행렬과 안정적인 지수 매개변수화를 도입한 시점에서 성능이 크게 향상되었다는 것입니다. 이는 병렬화 및 효율적인 계산을 통해 학습 속도와 성능이 동시에 개선된 것을 나타냅니다.
Performance on LRA tasks (LRA 과제에서의 성능) :
- 그래프의 Y축은 테스트 정확도를 나타내며, 각 색상과 기호는 서로 다른 과제를 의미합니다.
  - sCIFAR (오렌지색 원), ListOps (초록색 삼각형), PathFinder (갈색 사각형), PathX (노란색 다이아몬드)
- S4와 S5 모델의 성능은 대시 선으로 나타내어, 각 과제에서 LRU가 S4/S5와 동등한 성능을 발휘하고 있음을 보여줍니다.

각 3. Designing Performant Deep RNNs의 각 절에서는 논문에서 제안하는 Linear Recurrent Unit (LRU)의 핵심적인 설계 요소들을 설명합니다.

3.1 Linear RNN layers are performant (선형 RNN 레이어는 성능이 뛰어남)

이 절에서 연구진은 RNN의 비선형성을 제거하는 것이 성능 향상에 어떻게 기여하는지 설명합니다. RNN의 전통적인 구조는 tanh나 ReLU와 같은 비선형 활성화 함수가 포함되어 있지만, 논문에서는 이러한 비선형성을 제거한 선형 RNN (Linear RNN)이 매우 좋은 성능을 발휘할 수 있다는 점을 발견했습니다.

발견된 성능 개선: 실험 결과에 따르면 RNN의 비선형성을 제거한 후, Long Range Arena(LRA) 벤치마크에서 성능이 크게 개선되었습니다. 특히, 텍스트 처리나 정보 검색과 같은 특정 과제에서는 비선형 RNN보다도 더 나은 성능을 보였습니다.
비선형성 제거의 효과: 비선형성을 제거하면 RNN이 훨씬 더 효율적으로 작동하며, 특히 긴 시퀀스에서의 기울기 소실(vanishing gradient) 문제를 완화할 수 있습니다. 또한, 비선형성이 없는 상태에서 RNN을 쌓아 올리는 것이 비선형성을 유지하는 경우보다 더 쉽게 병렬화할 수 있습니다.

이 섹션에서의 주요 결론은, RNN에서 비선형성을 제거하는 것이 성능에 부정적인 영향을 미치지 않으며, 오히려 선형 반복(Linear Recurrence)이 복잡한 시퀀스-시퀀스 맵을 모델링할 수 있다는 점입니다. 이는 SSM이 선형 반복을 통해 좋은 성능을 내는 이유와도 관련이 있습니다.

3.2 Using complex diagonal recurrent matrices is efficient (복소 대각 반복 행렬 사용의 효율성)

다음 단계에서는 RNN의 반복 행렬을 복소수 대각 행렬(complex diagonal recurrent matrices)로 재구성하여 효율성을 크게 개선하는 방법을 설명합니다.

복소수 대각 행렬의 장점: RNN의 선형 레이어를 복소수 대각 행렬로 변환하면, 이 행렬은 더 쉽게 병렬화할 수 있습니다. 복소 대각 행렬은 행렬의 고유값 분해(eigen decomposition)를 통해 쉽게 처리할 수 있으며, 각 타임스텝에서의 계산을 병렬로 수행할 수 있습니다. 이는 학습 속도를 크게 높이며, 특히 긴 시퀀스를 처리하는 경우 유리합니다.
병렬화와 속도 향상: 복소수 대각 행렬을 사용하면, 선형 RNN의 학습과 추론을 병렬화할 수 있어 계산 비용을 줄일 수 있습니다. 기존의 비선형 RNN은 학습 시 순차적으로 계산이 이루어져야 하지만, 복소수 대각 행렬을 사용하면 병렬 계산이 가능하므로 학습 속도와 추론 속도가 크게 향상됩니다.

논문에서는 이 과정이 SSM에서도 자주 사용되는 기술임을 강조하며, 복소 대각 행렬이 복잡한 시퀀스 모델링에서 효율성을 높이는 데 큰 역할을 한다고 설명합니다.

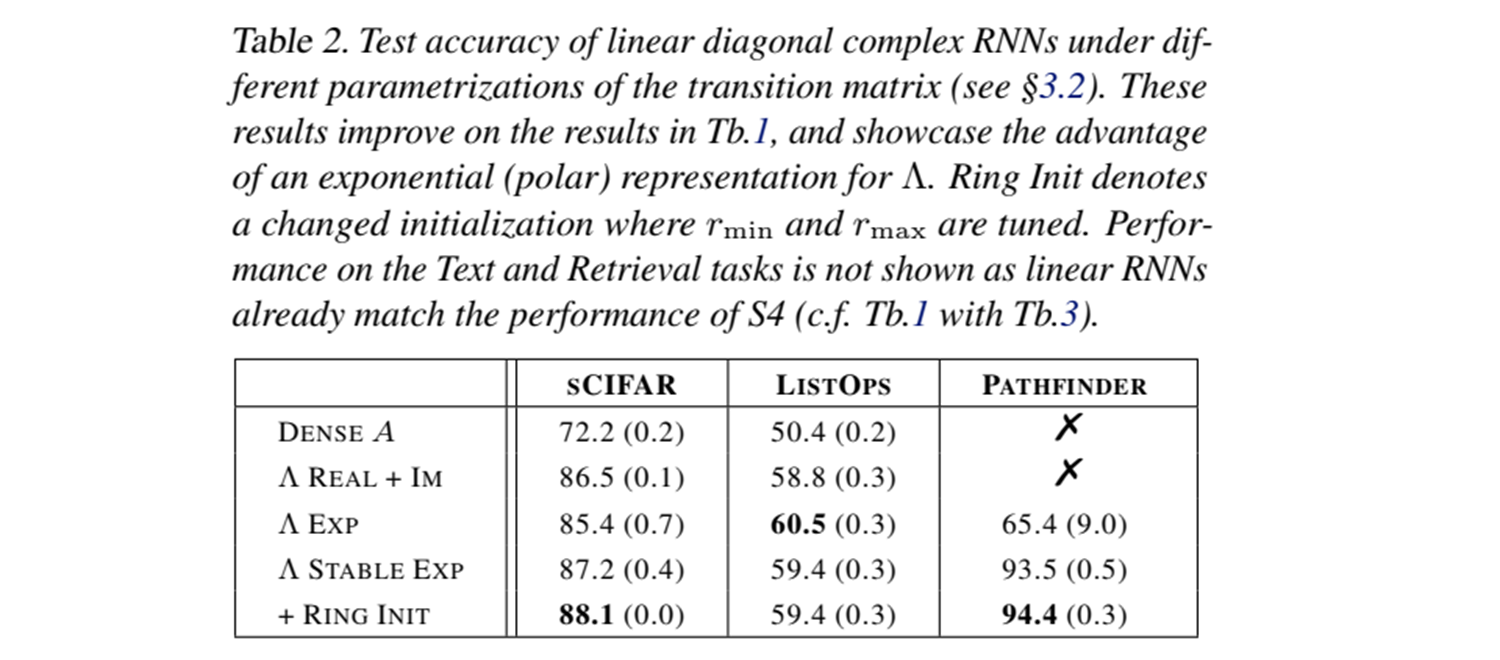
3.3 Stable Exponential Parameterization (안정적인 지수 매개변수화)

다음으로 논문에서는 지수 매개변수화(exponential parameterization)를 사용하여 반복 행렬의 안정성(stability)을 보장하는 방법을 설명합니다.

지수 매개변수화의 이점: 반복 행렬을 지수 함수로 매개변수화하면, 학습 중 모델의 안정성을 유지할 수 있습니다. 이는 특히 긴 시퀀스에서 반복적으로 상태를 업데이트할 때, 기울기의 소실이나 폭발 문제를 방지하는 데 매우 유용합니다.
고유값 분포와 성능 향상: 실험 결과에 따르면, 반복 행렬의 고유값 분포를 적절히 초기화하면 모델이 긴 시퀀스 의존성을 더 잘 학습할 수 있으며, 이는 SSM에서 성능이 뛰어난 이유 중 하나입니다. SSM에서 복잡한 초기화 규칙을 사용하는 대신, 고유값의 분포를 조정하여 학습 성능을 높일 수 있다는 점을 보여줍니다.

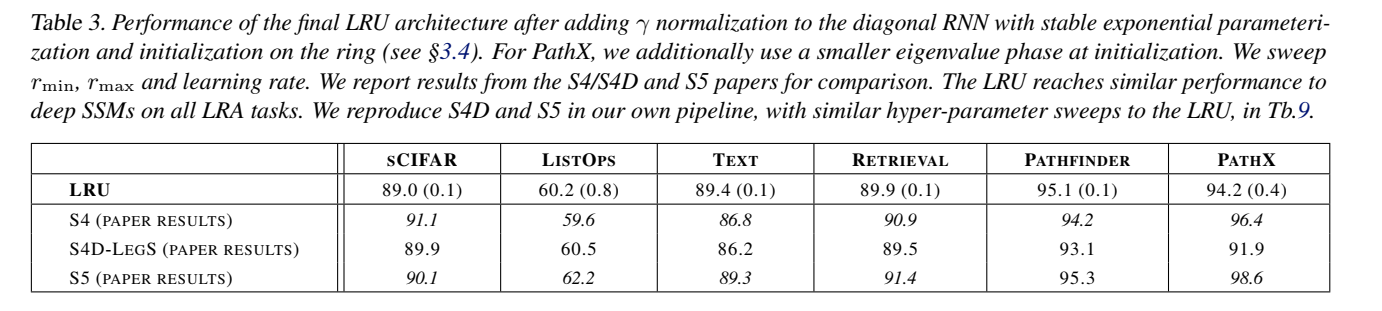
3.4 Normalization (정규화)

마지막으로 논문에서는 정규화(Normalization)의 중요성을 설명합니다. 긴 시퀀스 데이터를 학습할 때, RNN의 은닉 상태를 적절하게 정규화하는 것이 매우 중요합니다.

정규화의 역할: RNN은 은닉 상태를 순차적으로 업데이트하며 학습을 진행하는데, 긴 시퀀스를 처리하는 과정에서 은닉 상태가 과도하게 커지거나 작아질 수 있습니다. 이로 인해 모델이 학습하기 어려워질 수 있으므로, forward pass에서 은닉 상태를 정규화하는 것이 필수적입니다.
정규화와 성능 향상: 정규화를 적절히 적용하면 긴 시퀀스에서 RNN이 더 안정적으로 학습할 수 있으며, 이는 논문에서 제안하는 LRU 구조가 SSM과 유사한 성능을 발휘할 수 있는 이유 중 하나입니다. 또한, 정규화는 S4 모델에서 사용되는 구조와도 연결되며, 이 과정이 SSM에서 성능을 극대화하는 데 기여합니다.

4. Insights on S4 and Variants

논문에서 언급되는 S4 모델과 그 변형들(S4 and Variants)에 대한 인사이트는 주로 S4 모델이 뛰어난 성능을 발휘하는 원인과 이 모델의 특징에 대한 이해를 바탕으로 하고 있습니다.

1. S4의 구조적 효율성

인사이트: S4와 그 변형 모델들(DSS, S4D, S5 등)은 시퀀스 길이에 따라 연산 복잡도를 낮추는 효율적인 구조를 가지고 있습니다.
이유: S4는 Transformer의 attention 레이어가 가지는 $O(L^2)$ 메모리와 계산 복잡도를 피할 수 있습니다. S4는 순차적으로 토큰 간의 상호작용을 모델링하며, 이를 통해 긴 시퀀스를 효율적으로 처리할 수 있습니다. 또한, 순차적 모델임에도 불구하고 훈련 시 병렬 처리가 가능하여 학습 속도가 빠릅니다.

2. 선형 재귀 구조의 장점

인사이트: S4는 재귀적 연산을 선형적으로 처리하므로 RNN처럼 긴 시퀀스에 대한 정보 전파를 빠르게 수행할 수 있습니다.
이유: S4의 재귀적 레이어는 비선형성이 없는 선형 시스템으로 구성되며, 이는 학습이 보다 안정적이고 빠르게 이루어지게 합니다. 이 선형성은 RNN과 유사한 성질을 가지지만, 병렬 훈련이 가능하다는 점에서 큰 장점을 가집니다.

3. 복소 대각 행렬 사용의 이점

인사이트: S4는 복소수 대각 행렬을 사용함으로써 모델의 안정성과 성능을 높일 수 있습니다.
이유: 복소수 대각 행렬을 사용하면 모델이 더 많은 정보를 학습할 수 있으며, 연산 효율도 크게 향상됩니다. 특히 복소수 파라미터를 이용하여 모델 초기화를 안정적으로 설정하고, 훈련 시 장기 의존성 문제를 해결할 수 있습니다.

4. 특정 초기화의 중요성

인사이트: S4 모델의 성능 향상은 특정한 초기화 방법에서 기인하지만, 이러한 초기화가 항상 결정적인 것은 아닙니다.
이유: 초기화는 모델이 장기적인 의존성을 학습하는 데 중요하지만, 논문에서는 이 초기화 규칙이 항상 이론적으로 최적은 아닐 수 있으며, 다른 방법으로도 유사한 성능을 얻을 수 있다고 주장합니다.

5. 훈련 속도 및 성능의 균형

인사이트: S4 모델은 긴 시퀀스를 다룰 때도 빠른 학습 속도를 유지하며, 성능을 잃지 않는 균형점을 찾았습니다.
이유: S4의 설계는 RNN과 유사하지만 훈련 시 병렬 처리를 통해 학습 속도를 높일 수 있으며, 복잡한 모델의 성능을 유지하면서도 빠른 훈련을 가능하게 합니다.

결론적으로, 이 논문은 S4 모델과 그 변형들이 높은 성능을 달성하는 데 필요한 다양한 기하학적 및 계산적 요소들을 분석하고, 기존의 가정이 더 간단한 방법으로도 검증될 수 있음을 제시하고 있습니다.

이러한 인사이트는 향후 RNN 및 SSM 모델 개발에 중요한 방향성을 제공할 것으로 기대된다고 하며 글을 마무리합니다.

서쿠

Always be passionate ✨

이전 포스트

[개념] 시스템, 미분방정식, 그리고 상태 공간 모델

다음 포스트