시계열 데이터를 효율적으로 처리하는 방법은 지난 몇 년 동안 빠르게 발전했습니다. 특히, CMU에 계신 Albert Gu 교수님은 긴 시계열 의존성(Long-Range Dependencies, LRDs)을 처리하는 데 집중한 HiPPO(2020), LSSL(2021), 그리고 S4(2022)와 같은 연구들을 하고 계십니다.

이번 글에서는 연구의 흐름과 각 모델의 기술적 배경과 주요 기여를 설명하고, 어려운 개념들을 풀어봅니다. 이미지들은 아래 Reference에 적어둔 강의, 블로그 또는 논문에에서 발췌하여 편집 또는 사용하였습니다.

---

Backgrounds

1. Sequence Modeling의 필요성

Sequence Modeling은 시간에 따른 데이터의 패턴을 분석하고 예측하는 데 필수적인 기술입니다. 예를 들어, 음성 인식, 금융 시계열 분석, 바이오 신호 분석 등 다양한 분야에서 이러한 기술이 활용됩니다. 특히, 긴 시퀀스(long sequences)를 다루는 모델은 이러한 데이터를 효과적으로 처리하고 중요한 정보를 추출하는 데 중점을 둡니다.

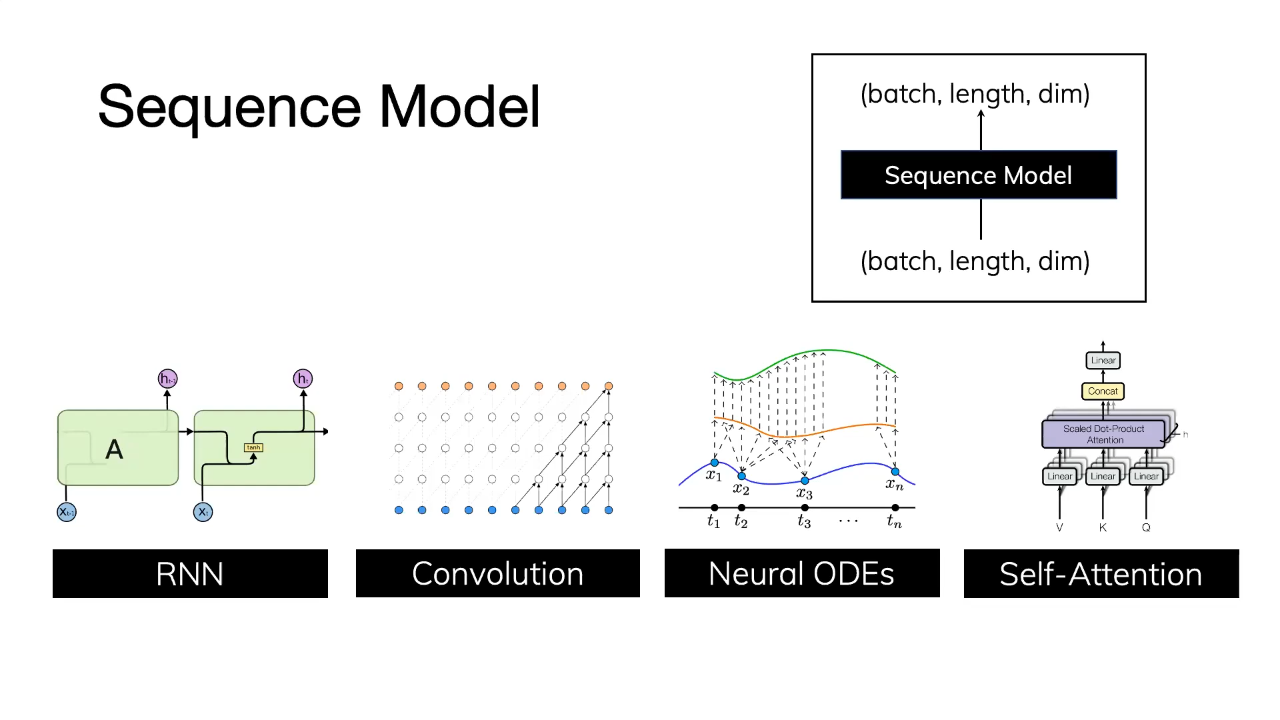
2. Sequence Modeling의 주요 과제

긴 시퀀스를 다루는 과정에서 두 가지 주요 과제가 있습니다.

• 첫째, 데이터의 시간적 연속성(time continuity)을 유지하면서도 이를 효과적으로 처리할 수 있는 모델이 필요합니다.
• 둘째, 학습 과정에서 발생하는 Vanishing Gradient 문제를 해결해야 합니다.

이는 RNN이나 기존의 순차 모델들이 긴 시퀀스에서 발생하는 공통적인 문제로, 시간에 따라 신호가 점차 약해져 모델 학습에 어려움을 줍니다.

3. State Space Model(SSM) 소개

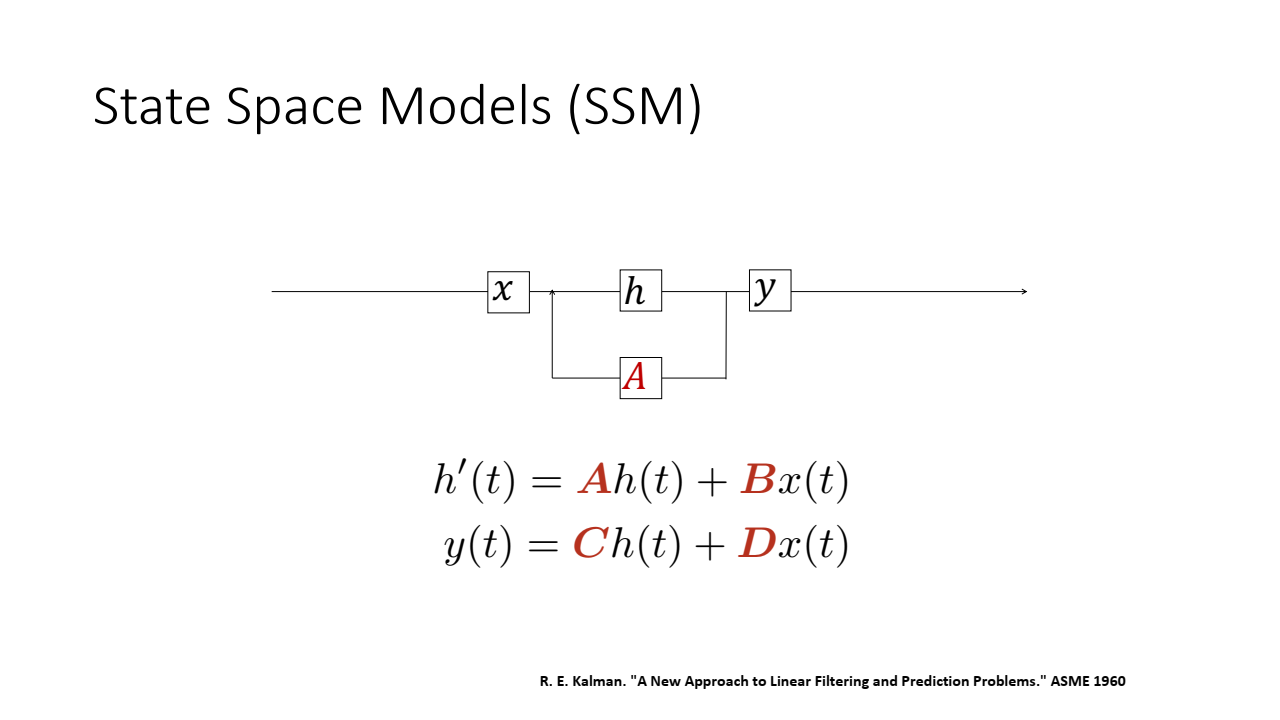
State Space Model(SSM)은 본래 제어 이론에서 유래한 모델로, 시스템의 상태(state)와 출력을 수학적으로 정의한 것입니다. 이 모델은 입력 데이터($x$)를 받아 상태($h$)를 계산한 후 이를 출력($y$)으로 변환하는 두 가지 주요 방정식으로 정의됩니다.

• SSM은 크게 3가지 Representation으로 표현될 수 있습니다:
  1. 연속 표현 (Continuous Representation)
  2. 순차적 표현 (Recurrent Representation)
  3. 합성곱 표현 (Convolution Representation)

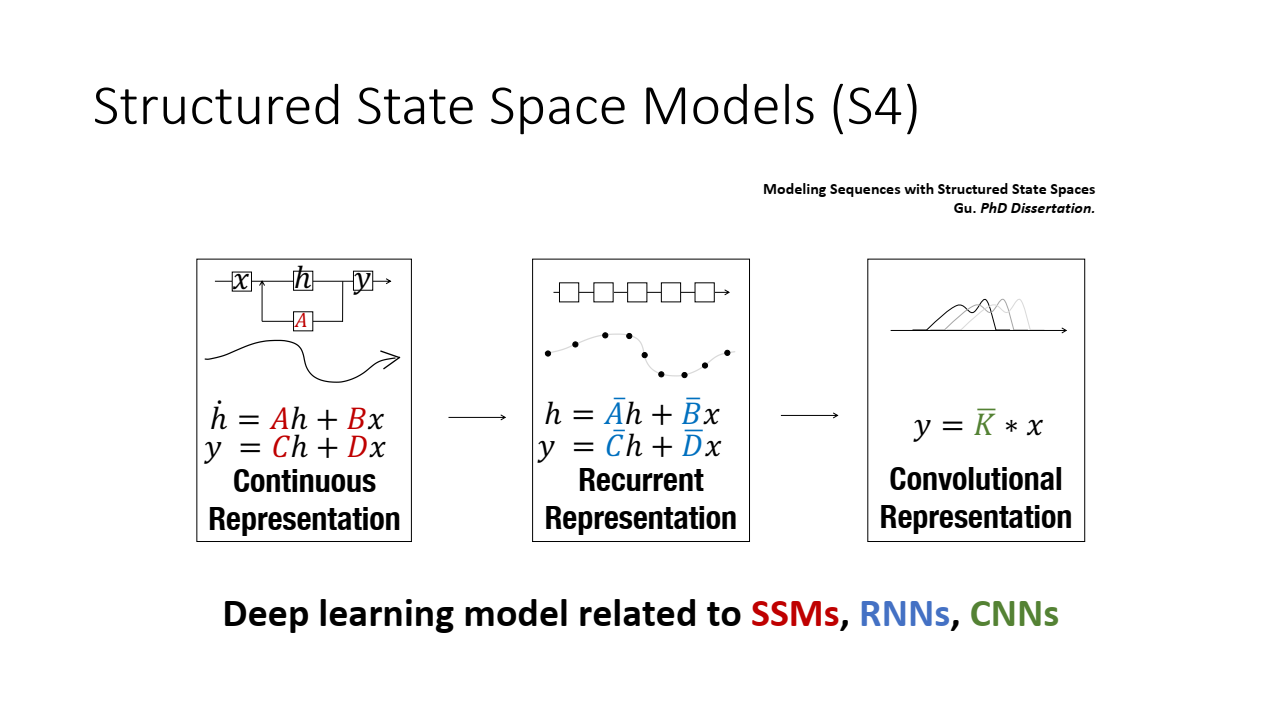
1. 연속 표현 (Continuous Representation)

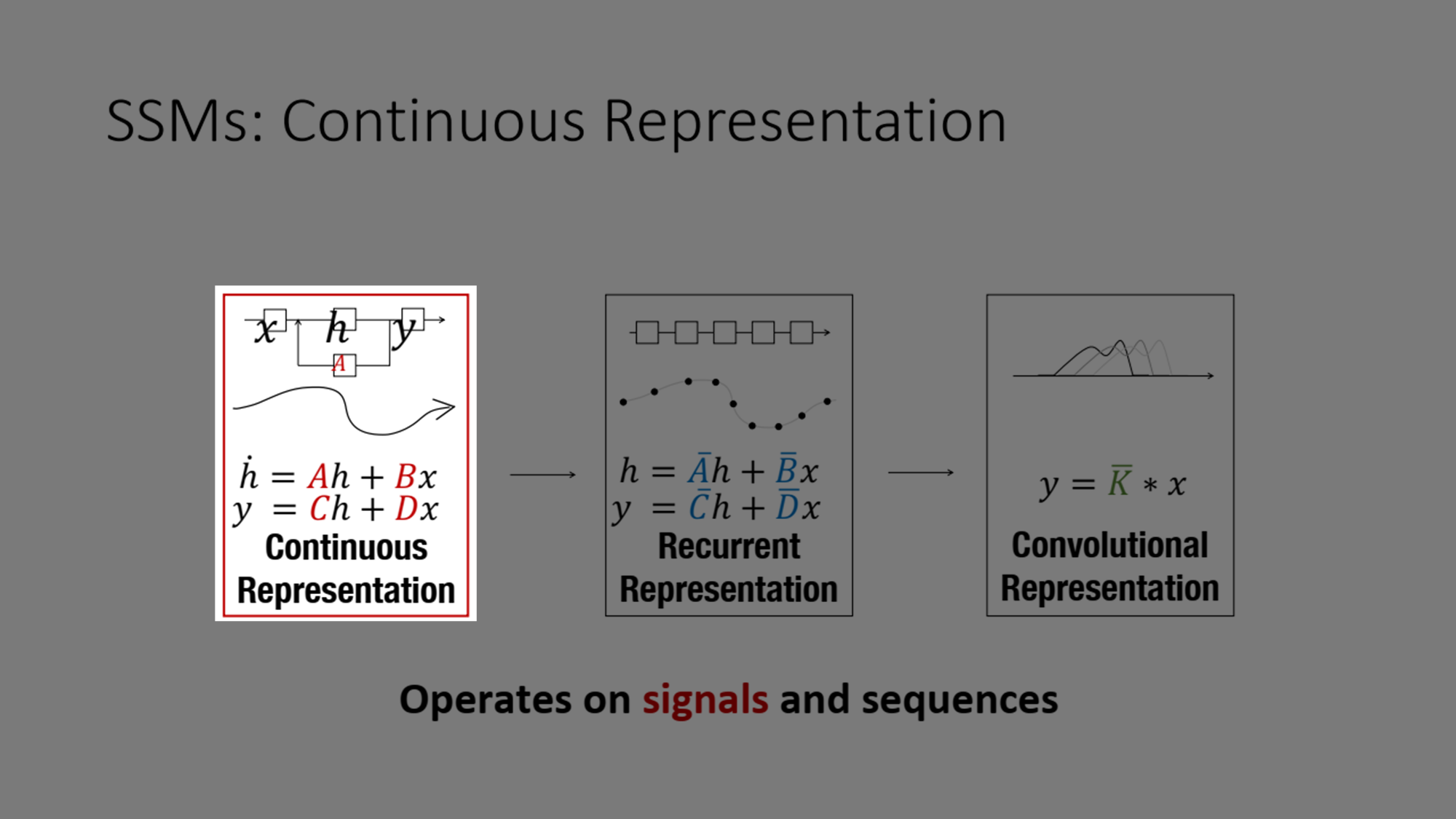
가장 먼저 SSM은 연속 표현(continuous Representation)을 처리할 수 있으며, 이를 통해 시퀀스 데이터의 연속성을 자연스럽게 모델링할 수 있습니다.

SSM의 주요 수학적 표현은 다음과 같습니다:

• 상태 방정식: $h'(t) = Ah(t) + Bx(t)$
• 출력 방정식: $y(t) = Ch(t) + Dx(t)$

이 방정식을 기반으로, SSM은 입력 시퀀스가 주어졌을 때 이를 처리하여 연속적인 출력을 생성하는 모델입니다.

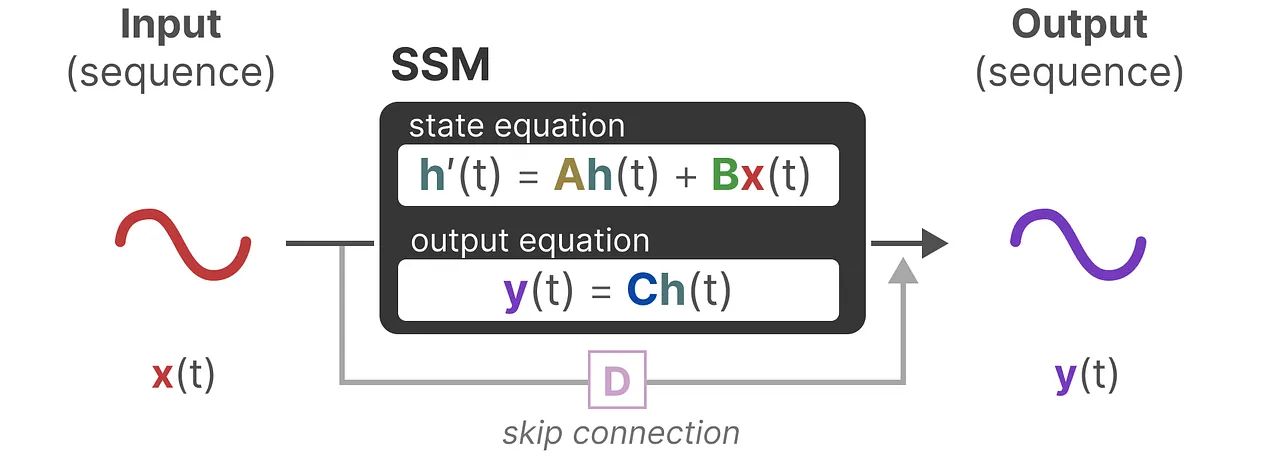
하지만, 여기서 반환되는 y는 연속된 시계열 표현(continuous-time representation)입니다. 이를 기계 또는 사람이 이해할 수 있는 범주로 가져오기 위해서는 Discrete Signal로 discretization(이산화) 작업을 수행해야합니다.

🔎 이산화란?
이산화(離散化, discretization)는 응용수학에서, 연속적인 함수, 모델, 변수, 방정식을 이산적인 구성요소로 변환하는 프로세스(process)이다. 이 프로세스는 일반적으로 디지털 컴퓨터에서 수치적 평가 및 구현에 적합하도록 하는 첫 단계로 수행된다.

---

2. Recurrent Representation

다음으로 Recurrent Representation은 상태 공간 모델에서 순차적으로 상태 $h_k$를 업데이트하는 구조입니다. 즉, $k$-번째 시간 단계에서의 상태 $h_k$는 이전 상태 $h_{k-1}$에 의존합니다.

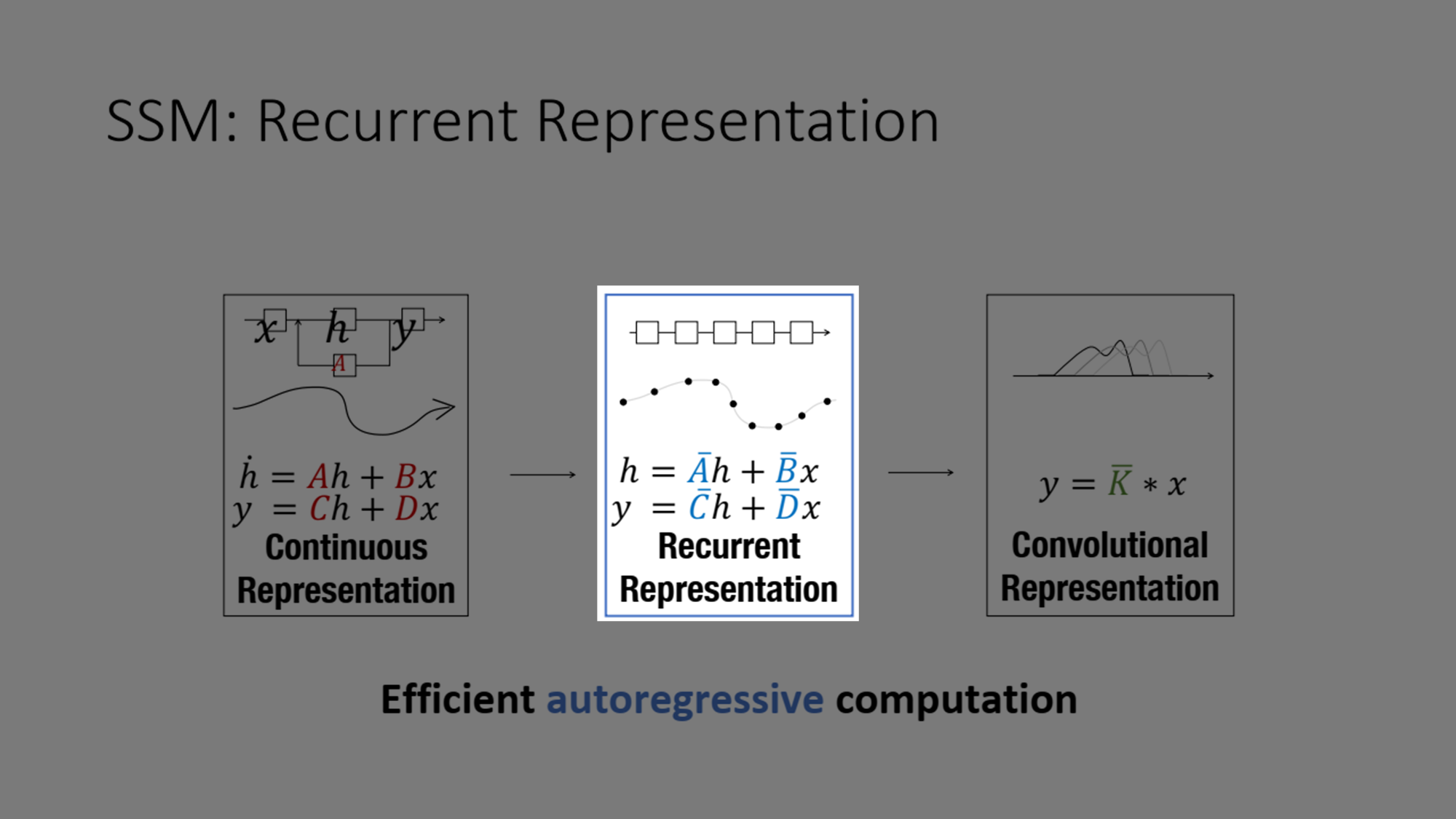
위 그림을 보시면 이전에 실선으로 이어진 그래프와는 다르게 지금의 그래프는 작게 작게 블록으로 나뉜 것을 보실 수 있죠? 이것은 데이터가 이산화되었기 때문입니다.

어디선가 많이 본 그림아닌가요? 바로 RNN의 모양과 유사한 것을 확인할 수 있습니다.

논문에서는 이산화를 위해 Zero-order hold (ZOH)이라는 기법을 사용합니다. ZOH는 디지털 신호를 아날로그 신호로 변환하는 과정에서 사용되는 중요한 기법으로, 각 샘플링 주기 동안 신호 값을 일정하게 유지하는 방법입니다.

✍️ ZOH의 수학적 표현은 다음과 같습니다:

$x_{\text{ZOH}}(t) = \sum_{n=-\infty}^{\infty} x[n] \cdot \text{rect}\left(\frac{t-T/2-nT}{T}\right)$

여기서:

• $x[n]$은 이산 시간 입력 신호
• $T$는 샘플링 주기
• $\text{rect}(\cdot)$는 직사각형 함수

(ZOH기반) 연속 시간 SSM을 이산 시간 SSM으로 변환

1. 연속 시간 SSM:

• $h'(t) = Ah(t) + Bx(t)$
• $y(t) = Ch(t) + Dx(t)$

2. ZOH 가정:

• $x(t) = x(k\Delta t) \quad \text{ , for} \quad k\Delta t \leq t < (k+1)\Delta t$

3. 상태 방정식 해결:

• $h(t) = e^{A(t-k\Delta t)}h(k\Delta t) + \int_{k\Delta t}^t e^{A(t-\tau)}Bx(k\Delta t)d\tau$

4. 이산 시간 모델 도출:

• $h_{k+1} = \bar{A}h_k + \bar{B}x_k$

• $y_k = Ch_k + Dx_k$

  여기서,

  • $\bar{A} = e^{A\Delta t}$
  • $\bar{B} = A^{-1}(e^{A\Delta t} - I)B$

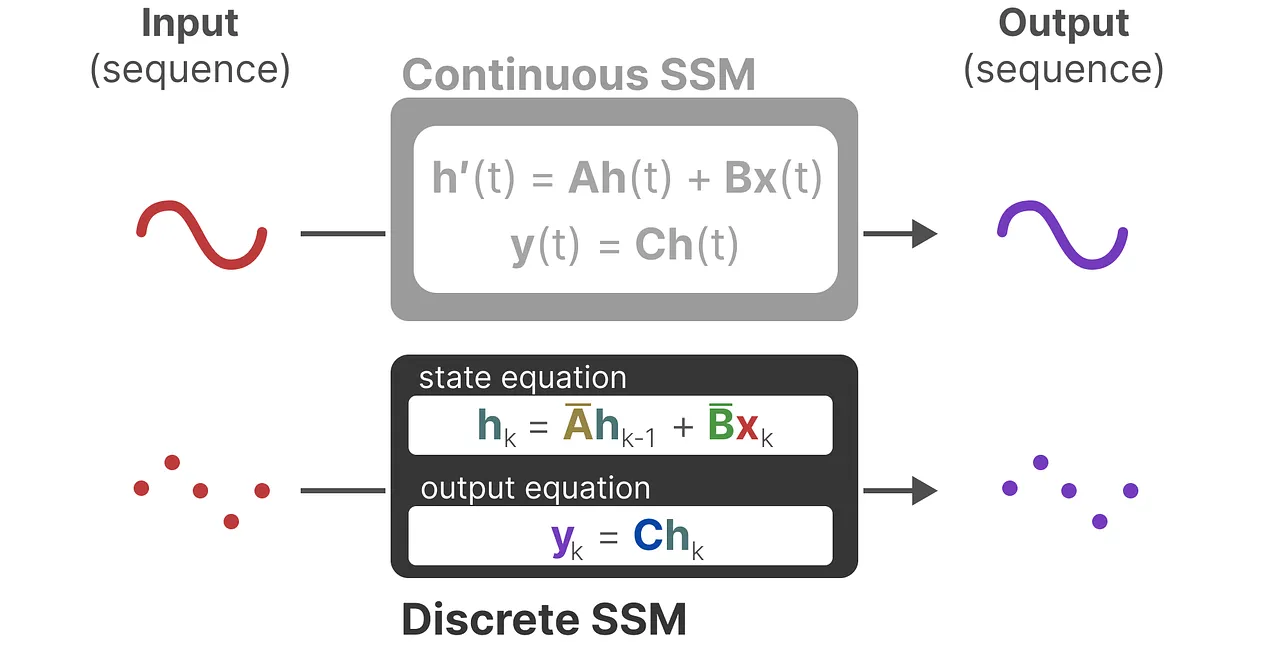
이제 이산화한 결과를 살펴보면 다음과 같이 각각의 T=0, T=1, T=2에 대해서 이전 time k-1의 $h_{k-1}$의 input과 현시점 $x_k$의 input을 받아서 $h_k$를 도출하고 이를 통해 $y_k$를 재귀적으로 호출하는 것을 볼 수 있습니다.

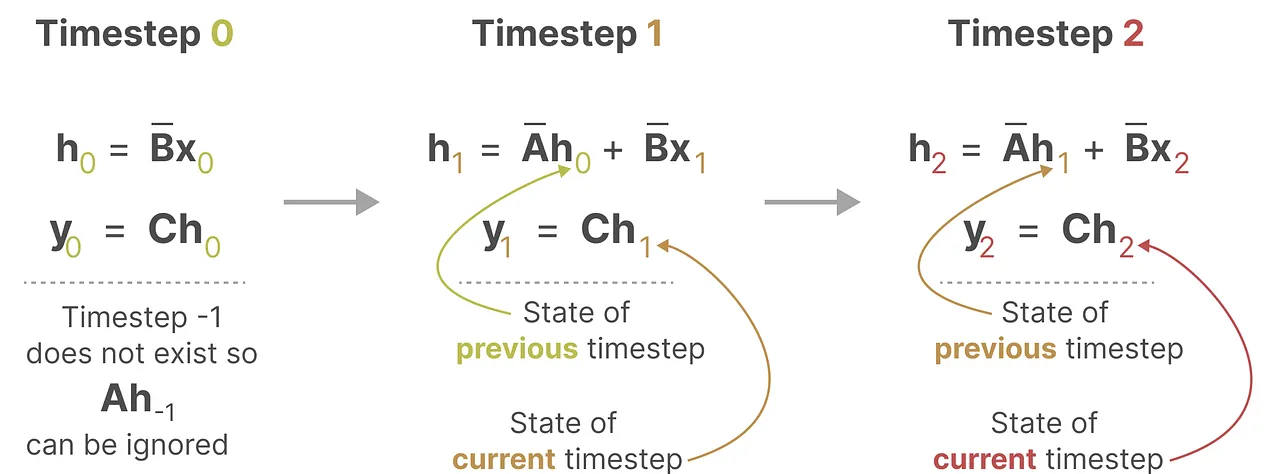
바로 RNN과 유사한 형태로 말이죠!!

---

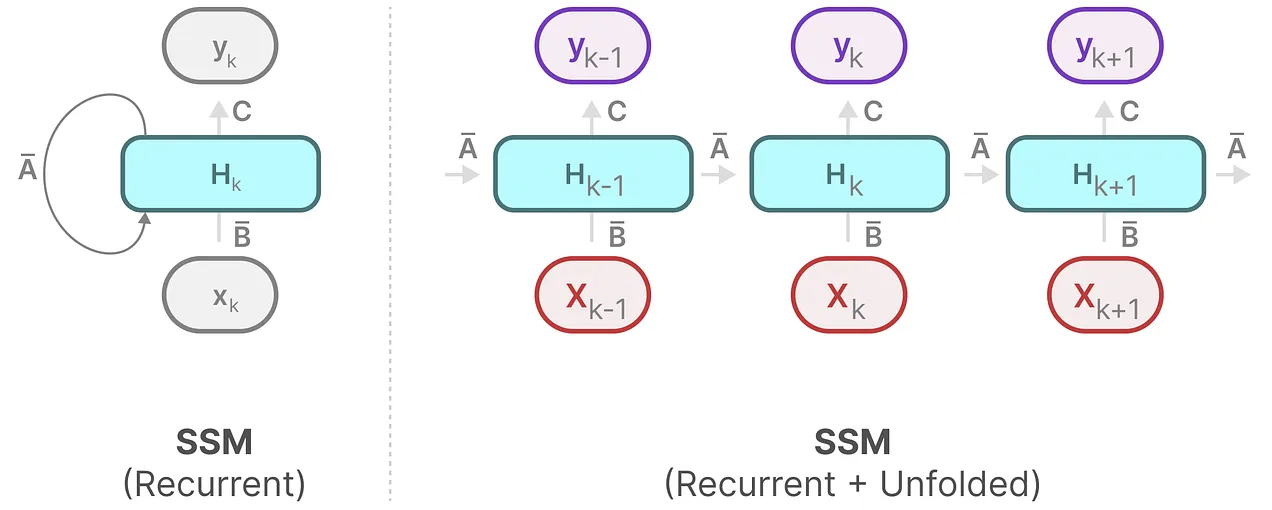
3. Convolution Representation

Recurrent Representation의 순차적인 상태 업데이트를 Convolution Representation으로 바꾸기 전에 먼저 시간 순으로 $h_k$를 살펴보겠습니다.

예를 들어,

• 첫 번째 상태(k=1)는 다음과 같습니다:

  • 상태 $h_1$:
    $h_1 = \bar{A} h_0 + \bar{B} x_0$
  • 출력 $y_1$:
    $y_1 = C h_1 + D x_0 = C(\bar{A} h_0 + \bar{B} x_0) + D x_0$

• 두 번째 상태(k=2)는 다음과 같습니다:

  • 상태 $h_2$:
    $h_2 = \bar{A} h_1 + \bar{B} x_1 = \bar{A}^2 h_0 + \bar{A} \bar{B} x_0 + \bar{B} x_1$
  • 출력 $y_2$:
    $y_2 = C h_2 + D x_1 = C(\bar{A}^2 h_0 + \bar{A} \bar{B} x_0 + \bar{B} x_1) + D x_1$

• 세 번째 상태(k=3)는 다음과 같습니다:

  • 상태 $h_3$:
    $h_3 = \bar{A} h_2 + \bar{B} x_2 = \bar{A}^3 h_0 + \bar{A}^2 \bar{B} x_0 + \bar{A} \bar{B} x_1 + \bar{B} x_2$
  • 출력 $y_3$:
    $y_3 = C h_3 + D x_2 = C(\bar{A}^3 h_0 + \bar{A}^2 \bar{B} x_0 + \bar{A} \bar{B} x_1 + \bar{B} x_2) + D x_2$

• 네 번째 상태(k=4)는 다음과 같습니다:

  • 상태 $h_4$:
    $h_4 = \bar{A} h_3 + \bar{B} x_3 = \bar{A}^4 h_0 + \bar{A}^3 \bar{B} x_0 + \bar{A}^2 \bar{B} x_1 + \bar{A} \bar{B} x_2 + \bar{B} x_3$
  • 출력 $y_4$:
    $y_4 = C h_4 + D x_3 = C(\bar{A}^4 h_0 + \bar{A}^3 \bar{B} x_0 + \bar{A}^2 \bar{B} x_1 + \bar{A} \bar{B} x_2 + \bar{B} x_3) + D x_3$

• 다섯 번째 상태(k=5)는 다음과 같습니다:

  • 상태 $h_5$:
    $h_5 = \bar{A} h_4 + \bar{B} x_4 = \bar{A}^5 h_0 + \bar{A}^4 \bar{B} x_0 + \bar{A}^3 \bar{B} x_1 + \bar{A}^2 \bar{B} x_2 + \bar{A} \bar{B} x_3 + \bar{B} x_4$
  • 출력 $y_5$:
    $y_5 = C h_5 + D x_4 = C(\bar{A}^5 h_0 + \bar{A}^4 \bar{B} x_0 + \bar{A}^3 \bar{B} x_1 + \bar{A}^2 \bar{B} x_2 + \bar{A} \bar{B} x_3 + \bar{B} x_4) + D x_4$

규칙이 좀 보이시나요?! 좀 더 이쁘게 제가 만든 그림을 밑에 보여드리겠습니다. (*D term은 생략함)

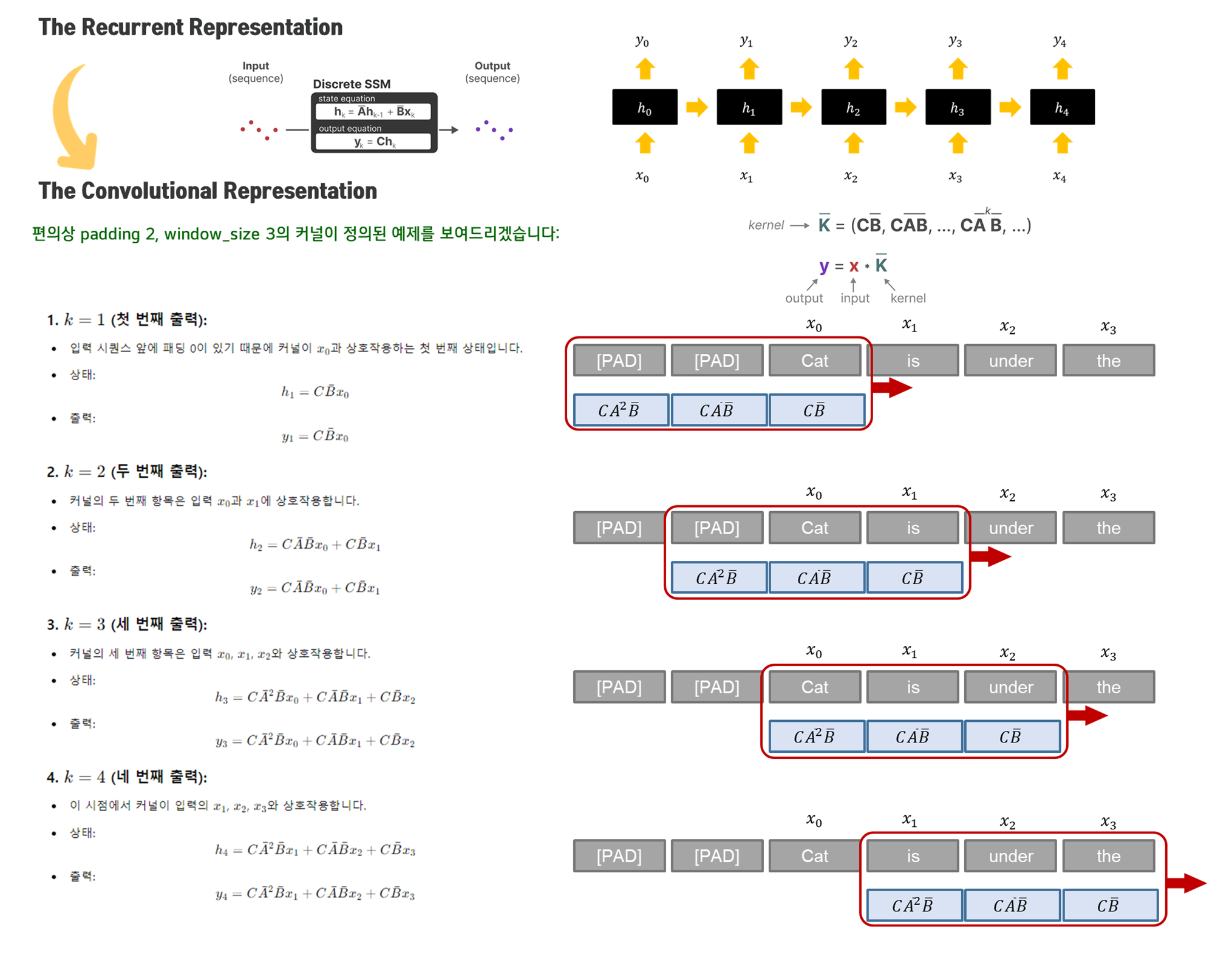
1. $k = 1$ (첫 번째 출력)

• 상태: $h_1 = C \bar{B} x_0$
  • 여기서 커널의 마지막 항목 $C \bar{B}$가 입력 $x_0$와 곱해져 첫 번째 출력 $y_1$가 계산됩니다.
  • 패딩이 있기 때문에 커널의 앞 두 항목은 입력과 상호작용하지 않고 패딩(0)에 해당합니다.
• 출력: $y_1 = C \bar{B} x_0$
  • 첫 번째 출력은 $C \bar{B} x_0$로 표현됩니다.

2. $k = 2$ (두 번째 출력)

• 상태: $h_2 = C \bar{A} \bar{B} x_0 + C \bar{B} x_1$
  • 이제 커널의 두 번째 항목이 $x_0$, 마지막 항목이 $x_1$과 곱해지면서 두 번째 상태가 계산됩니다.
  • 패딩 값이 하나 남아있고, 커널의 첫 번째 항목은 여전히 패딩(0)과 상호작용합니다.
• 출력: $y_2 = C \bar{A} \bar{B} x_0 + C \bar{B} x_1$
  • 두 번째 출력은 이전 입력과 현재 입력의 합으로 계산됩니다.

3. $k = 3$ (세 번째 출력)

• 상태: $h_3 = C \bar{A}^2 \bar{B} x_0 + C \bar{A} \bar{B} x_1 + C \bar{B} x_2$
  • 세 번째 상태에서는 커널의 모든 항목이 실제 입력과 상호작용하기 시작합니다.
  • 커널의 첫 번째 항목은 $x_0$, 두 번째 항목은 $x_1$, 세 번째 항목은 $x_2$와 곱해집니다.
• 출력: $y_3 = C \bar{A}^2 \bar{B} x_0 + C \bar{A} \bar{B} x_1 + C \bar{B} x_2$
  • 세 번째 출력은 $x_0$, $x_1$, $x_2$에 대한 커널 가중합으로 계산됩니다.

4. $k = 4$ (네 번째 출력)

• 상태: $h_4 = C \bar{A}^2 \bar{B} x_1 + C \bar{A} \bar{B} x_2 + C \bar{B} x_3$
  • 네 번째 상태에서는 커널이 $x_1$, $x_2$, $x_3$과 상호작용합니다.
  • 더 이상 패딩이 적용되지 않으며, 입력 시퀀스와 커널 간의 완전한 상호작용이 이루어집니다.
• 출력: $y_4 = C \bar{A}^2 \bar{B} x_1 + C \bar{A} \bar{B} x_2 + C \bar{B} x_3$
  • 네 번째 출력은 $x_1$, $x_2$, $x_3$에 대한 커널 가중합입니다.

Convolution Representation 방식의 장점은 Recurrent Representation에서 각 시간 단계별로 순차적으로 상태를 업데이트하는 대신, 모든 시간 단계의 출력을 한 번에 계산할 수 있다는 점입니다.

• 병렬 처리 가능: Recurrent Representation에서는 각 시간 단계별로 순차적으로 상태를 업데이트해야 하므로 계산이 직렬화되어 있습니다. 그러나 Convolution Representation에서는 커널을 이용하여 입력 시퀀스 전체에 걸쳐 동시에 출력을 계산할 수 있어, 병렬화가 가능해집니다. 이는 특히 긴 시퀀스를 처리할 때 효율적인 계산을 가능하게 합니다.

• 더 큰 커널 적용 가능: 예시에서는 커널 사이즈를 3으로 설정했지만, 이론적으로는 더 큰 커널도 사용할 수 있습니다. 더 큰 커널은 더 긴 범위의 과거 입력을 한 번에 처리할 수 있어, 더 넓은 문맥 정보를 활용할 수 있게 합니다. 이는 시퀀스 데이터에서 장기적인 종속성을 더 잘 반영하는 데 도움이 됩니다.

• 효율성: 합성곱 연산은 일반적으로 GPU와 같은 병렬화가 가능한 하드웨어에서 매우 빠르게 처리될 수 있습니다. 이는 Recurrent Representation에 비해 계산 속도에서 큰 이점을 제공합니다.

---

그러나, 이상적으로 이러한 deepSSM을 바로 적용하기에는 많은 문제점들이 있었는데요.

아래 연구들은 이런 Convolution Representation을 어떻게 효율적으로 계산하고 처리할 수 있는가에 대한 연구들입니다.

1. HiPPO : Recurrent Memory with Optimal Polynomial Projections (2020)
2. LSSL : Combining Recurrent, Convolutional, and Continuous-time Models with Linear State-Space Layers (2021)
3. S4 : Efficiently Modeling Long Sequences with Structured State Spaces (2022)

---

Research

이 논문들은 각각 시계열 데이터를 다루는 기존 모델의 한계를 극복하는 중요한 기술적 발전을 담고 있습니다.

1. HiPPO: Recurrent Memory with Optimal Polynomial Projections (NeurIPS, 2020)

   • 목적: 긴 시퀀스에 대한 메모리 문제를 해결하고, 메모리를 효율적으로 유지하면서 입력 정보를 계속 업데이트하는 방법을 제안합니다.
   • 효과: 이 연구는 메모리 효율성과 정보 유지 간의 균형을 찾는 데 초점을 맞춥니다. 이를 통해 긴 시퀀스에서도 정보를 효과적으로 처리할 수 있게 됩니다.

2. LSSL: Combining Recurrent, Convolutional, and Continuous-time Models with Linear State-Space Layers (NeurIPS, 2021)

   • 목적: 이 연구는 연속 시간 모델과 선형 상태 공간 레이어(LSSL)를 결합하여, 시간에 따른 연속적인 변화와 비연속적인 변화를 동시에 처리할 수 있게 만듭니다.
   • 효과: LSSL은 모델의 유연성을 높여서, 시계열 데이터뿐 아니라 다양한 종류의 연속적 데이터를 처리할 수 있도록 돕습니다.

3. S4: Efficiently Modeling Long Sequences with Structured State Spaces (ICLR, 2022)

   • 목적: S4는 Convolution Representation의 효율성을 극대화하면서도, 장기적인 종속성을 더 잘 처리할 수 있게 최적화되었습니다.
   • 효과: S4는 특히 장기적인 패턴 학습에 강점이 있어, 기존의 모델보다 훨씬 긴 시퀀스에서도 우수한 성능을 보입니다.

---

1. HiPPO: Recurrent Memory with Optimal Polynomial Projections (Neurips 2020)

Preliminary

본격적으로 HiPPO를 살펴보기에 앞서, 다음 수학 개념들을 어느 정도 이해하고 있어야 관련 내용을 더 잘 이해할 수 있습니다: 라게르(Laguerre) 다항식, 르장드르(Legendre) 다항식, 그리고 다항식 투영 연산자입니다. 이 개념들은 시계열 데이터를 분석하고 근사하는 데 중요한 역할을 하며, 복잡한 데이터를 수학적으로 다루는 강력한 도구입니다. 각 개념을 차례로 설명하겠습니다.

1. 다항식 투영 연산자(Polynomial Projection Operator)

• 다항식 투영 연산자는 복잡한 데이터를 특정 직교 다항식 기저를 사용하여 더 간단한 다항식으로 표현하는 과정입니다. 시계열 데이터나 함수가 주어졌을 때, 이를 직교하는 다항식들의 선형 결합으로 근사합니다.

💡 직교 다항식 기저(Orthogonal Polynomial Basis)는 여러 다항식 중에서도 서로 직교(orthogonal)하는 성질을 가진 다항식들의 집합을 의미합니다.

• 직교성은 두 함수(또는 두 다항식) 사이의 내적(inner product)이 0이라는 의미입니다. 직교성은 데이터나 함수의 서로 다른 성분이 서로 영향을 미치지 않는 독립적인 관계를 나타냅니다.
• 기저란 주어진 공간을 구성하는 "기본" 요소들의 집합을 의미합니다. 기저 벡터의 선형 결합을 통해 공간 내의 모든 벡터(또는 함수)를 표현할 수 있는 것처럼, 기저 다항식을 사용하면 주어진 함수나 데이터를 그 기저 다항식들의 선형 결합으로 표현할 수 있습니다.
  • 3차 다항식 공간에서는 다음과 같은 기저를 생각할 수 있습니다:
    $1, x, x^2, x^3$
  • 3차 이하의 모든 다항식은 이들의 선형 결합으로 표현될 수 있습니다:
    $f(x) = a_0 + a_1 x + a_2 x^2 + a_3 x^3$

• 다항식 투영의 핵심 : 주어진 함수나 데이터를 직교 다항식 기저 위에 "투영"하여 가장 적합한 근사값을 찾는 것입니다. 직교 다항식은 서로 독립이기 때문에, 데이터를 여러 개의 독립적인 성분으로 분해하여 분석하는 것이 가능합니다.

• 오차 최소화 : 투영 연산자는 보통 최소 제곱법(least squares method)을 사용하여 주어진 데이터를 다항식 기저로 표현하는 과정에서 오차를 최소화합니다.

일반적으로 "내적!" 하면 고등학교에서 배운 $a \cdot b = |a| |b| \cos\theta$ 가 생각나실겁니다. 하지만, 함수 간의 내적은 이를 확장한 개념으로 단순히 각도나 크기와 같은 직관적인 개념으로 설명되지 않습니다.

💬 (REVIEW) 벡터 내적 : $a \cdot b = |a| |b| \cos\theta$

• $a$와 $b$는 벡터입니다.
• $|a|$와 $|b|$는 각 벡터의 길이(크기, magnitude)입니다.
• $\theta$는 두 벡터 사이의 각도입니다.
• 두 벡터의 내적은 두 벡터 사이의 유사도를 측정하는데, 벡터가 평행할수록 내적의 값은 크고, 직교(즉, 90도일 때)할수록 내적은 0이 됩니다.

✨ (NEW) 함수 내적 : $\langle f, g \rangle = \int_a^b f(x) g(x) w(x) \, dx$

• $f(x)$와 $g(x)$는 함수입니다.
• $[a, b]$는 함수가 정의된 구간입니다.
• $w(x)$는 가중 함수로, 내적 계산에서 특정 구간에 가중치를 부여하는 역할을 합니다.
• 함수의 내적은 벡터 내적처럼 함수 사이의 유사도를 측정하는 역할을 합니다.

• 투영 연산자의 작동 방식:

  1. 기저 다항식 선택: 특정 구간에서 직교하는 다항식을 선택합니다.
     ↳ 예를 들어, 구간 [-1, 1]에서 르장드르 다항식, 구간 [0, ∞)에서 라게르 다항식을 사용할 수 있습니다. (아래 참고)
     
     
  2. 계수 결정: 다항식 투영 연산자는 주어진 데이터에 가장 적합한 다항식 기저의 계수를 찾아냅니다.
     ↳ 이를 통해 데이터를 표현하는 함수가 각 다항식의 선형 결합으로 나타납니다.
     
     
  3. 함수 근사: 투영된 결과는 원래 데이터에 대한 "최적의 근사"를 제공합니다.
     ↳ 이를 통해 데이터를 단순화하거나 분석할 수 있습니다.

2. 르장드르 다항식(Legendre Polynomials)

• 르장드르 다항식은 구간 [-1, 1]에서 가중 함수 $w(x) = 1$에 대해 직교성을 갖는 다항식입니다.

• 르장드르 다항식의 직교성은 다음 수식으로 표현됩니다:

  $\frac{2n+1}{2} \int_{-1}^{1} P_n(x) P_m(x) \, dx = \delta_{nm}$

• 이 수식은 서로 다른 차수의 르장드르 다항식들이 구간 [-1, 1]에서 직교함을 나타냅니다. 여기서:

  • $P_n(x)$와 $P_m(x)$는 각각 차수가 다른 르장드르 다항식입니다.
  • $\delta_{nm}$는 크로네커 델타로, $n = m$일 때는 1, 그렇지 않으면 0을 의미합니다. 즉, 같은 차수일 경우 내적이 1이 되고, 다른 차수일 경우 내적이 0이 됩니다.

• 또한, 르장드르 다항식은 다음과 같은 경계 조건을 만족합니다:

  $P_n(1) = 1, \quad P_n(-1) = (-1)^n$

  이는 르장드르 다항식의 값이 구간 끝점에서 어떻게 동작하는지를 보여줍니다.

• (참고) HiPPO에서는 Legendre 다항식이 시간 축에 따른 데이터를 압축하는 데 사용됩니다. 이를 통해 이전 시점에서의 데이터를 효과적으로 메모리에 저장하고 기억할 수 있습니다.

3. 라게르 다항식(Laguerre Polynomials)

• 라게르 다항식은 [0, ∞) 구간에서 가중 함수 $e^{-x}$에 대해 직교성을 갖는 다항식입니다.

• 라게르 다항식의 직교성은 다음 수식으로 표현됩니다:

  $\int_0^{\infty} x^\alpha e^{-x} L_n^{(\alpha)}(x) L_m^{(\alpha)}(x) \, dx = \frac{(n + \alpha)!}{n!} \delta_{nm}$

• 이 수식은 서로 다른 차수의 라게르 다항식들이 가중 함수 $e^{-x}$에 대해 직교함을 나타냅니다. 여기서:

  • $L_n^{(\alpha)}(x)$와 $L_m^{(\alpha)}(x)$는 각각 일반화된 라게르 다항식으로, 매개변수 $\alpha$에 따라 달라집니다.
  • $\delta_{nm}$는 크로네커 델타로, $n = m$일 때는 1, 그렇지 않으면 0입니다.

• 표준 라게르 다항식은 매개변수 $\alpha = 0$일 때의 특수한 경우로, 다음과 같은 직교성을 가집니다:

  $\int_0^{\infty} e^{-x} L_n(x) L_m(x) \, dx = \frac{(n)!}{n!} \delta_{nm} = \delta_{nm}$

• (참고) HiPPO에서는 Laguerre 다항식을 사용하여 과거 데이터를 표현하고 기억하는 방식으로, 특히 메모리 관리에 사용됩니다. 이 다항식은 시간이 지남에 따라 데이터가 어떻게 변하는지 모델링하는 데 적합합니다.

HiPPO Preliminary
HiPPO에서는 다항식 투영 연산자(Legendre 다항식과 Laguerre 다항식)을 통해 시간 축에 따른 데이터를 압축하고, 메모리 사용량을 줄이며, 중요한 정보를 요약하여 저장하는 방식으로 사용됩니다.

• 이 다항식들은 입력 데이터를 다항식 공간에 투영하여, 이전 시점의 데이터를 효율적으로 기억하고 업데이트하는 데 도움을 줍니다.

  • Legendre 다항식은 구간 [-1, 1] 내에서 시계열 데이터를 모델링하고, 직교성을 통해 메모리의 효율적인 관리가 가능합니다.
  • Laguerre 다항식은 주로 신호 처리에서 긴 시간에 걸쳐 데이터를 처리할 때 사용되며, HiPPO에서는 데이터를 요약하고 저장하는 데 사용합니다.

---

Introduction (서론)

• Introductin에서는 먼저 Sequential 데이터의 처리를 위한 현존하는 RNN 모델의 제약 사항들을 아래와 같이 서술합니다:

  1. Limited Memory Horizon: RNN은 긴 시퀀스를 처리할 때 이전 정보의 기억이 약해지는 경향이 있습니다. 즉, 모델이 이전 데이터에서 중요한 정보를 잊어버리는 문제에 직면하게 됩니다.

  2. Vanishing Gradients: RNN은 역전파 과정에서 기울기가 매우 작아져서 가중치 업데이트가 거의 이루어지지 않는 문제에 직면합니다. 이로 인해 모델이 장기 의존성을 학습하기가 매우 어려워집니다.

  3. 시퀀스 길이 및 시간 척도에 대한 선행 정보 요구: 기존 RNN 및 그 변형들은 특정한 시퀀스 길이나 시간 척도에 대한 선행 정보(prior)를 필요로 합니다. 그러나 이러한 선행 정보는 불확실한 환경이나 데이터 분포 변화에 대해 일반화하기 어렵습니다.

  4. 이론적 보장 결여(Theoretical Guarantees):

     • 기존 방법들은 장기 의존성을 얼마나 잘 캡처할 수 있는지에 대한 이론적 보장이 부족합니다. 특히, 기울기 경계 등과 같은 성능에 대한 이론적 근거가 결여되어 있어, 효과적인 성능을 기대하기 어렵습니다.

  5. 장기 및 복잡한 시간 의존성 모델링의 어려움: RNN은 복잡한 시간 의존성을 모델링하는 데 한계가 있으며, 이로 인해 의료 데이터와 같은 다양한 샘플링 주기를 가진 데이터에서 효과적으로 작동하지 못할 수 있습니다.

• 논문에서는 이러한 한계점을 해결하기 위해 HiPPO(High-order Polynomial Projection Operators)라는 새로운 프레임워크를 제안합니다.

• HiPPO는 연속 신호 및 이산 시계열 데이터를 최적의 방법으로 압축하고 과거 데이터를 모델링하여 장기 의존성을 잘 처리할 수 있도록 도와줍니다.

---

The HiPPO Framework: High-order Polynomial Projection Operators (HiPPO 프레임워크: 고차 다항식 투영 연산자)

HiPPO 프레임워크의 목표는 시간에 따라 변화하는 데이터를 압축된 형태로 유지하며, 각 시간 t에서 과거 데이터를 효율적으로 표현하는 것입니다.

• 이 프레임워크는 온라인 함수 근사를 통해 메모리 메커니즘을 고안하고, 고차 다항식 투영 연산자를 사용하는 방식으로 순차 데이터를 처리합니다

문제 정의

• 입력 함수 $f(t)$의 누적 이력을 온라인으로 압축하여 표현하는 방법을 논의합니다.

  • Online Approximation (온라인 근사):
    • 각 시간 $t$마다 $f_{\leq t}$를 근사하기 위해 측도 $\mu(t)$가 변화합니다.
    • 이 측도는 다양한 과거 입력의 중요도를 조절하며, 최적의 다항식 근사를 찾아내는 과정에서 활용됩니다.

• 함수의 역사 $f_{\leq t}$를 유지하기 위해서는 두 가지 필수 요소가 도출됩니다: 근사 방법과 서브스페이스.

  1. Function Approximation with respect to a Measure (측도에 대한 함수 근사):

     • 근사 품질을 정량화하는 방법은 확률 측도 $\mu$를 통해 내적을 정의하는 방식입니다.
     • 내적은 $\langle f, g \rangle_\mu = \int_0^\infty f(x) g(x) d\mu(x)$로 표현되며, 함수 $f$와 $g$ 사이의 거리 또는 오차를 측정할 수 있는 기준을 제공합니다.

  2. Polynomial Basis Expansion (다항식 기초 확장):

     • 다항식을 기반으로 한 부분 공간 $G$를 사용하여 함수를 근사합니다.
     • 이 부분 공간은 차수 $N$ 미만의 다항식으로 구성되며, 이는 입력 함수의 근사를 위해 사용할 수 있는 기준을 제공합니다.
     • 이러한 기초 확장은 다양한 함수들을 효과적으로 표현할 수 있는 기반을 제공합니다.

HiPPO 핵심 아이디어

1. Choose suitable basis (적절한 기저 선택)

• 의미:

  • 특정 함수 $f(t)$를 근사하기 위해, 그 함수의 공간에서 적절한 다항식 기저를 선택하는 단계입니다.
  • 이 기저는 함수의 성질과 시간 가변 측정 $\mu(t)$에 따라 달라지며, 일반적으로는 orthogonal 다항식이 사용됩니다.

• 세부 사항:

  • 선택된 기저 $\{g_n\}_{n < N}$는 $N$차원의 다항식 공간을 구성하며, 이 기저에 대해 함수 $f_{\leq t}$를 projection 합니다.
  • 이는 주어진 함수와 기저의 관계를 정의하기 위한 것입니다. 최적의 계수 $c(t)$는 다음과 같은 내적을 통해 계산됩니다:
    $c(t)_n := \langle f_{\leq t}, g_n \rangle_{\mu(t)}$
  • 이 단계의 목적은 입력 신호의 중요한 특성들을 보존하면서 복잡한 함수를 그 기저에 맞춰 간단한 다항식으로 표현하는 것입니다.

2. Differentiate the projection (프로젝션 미분)

• 의미:

  • 선택한 기저에 대해 시간 $t$에 따라 projection을 미분하는 단계입니다.
  • 이는 주어진 함수의 시간적 변화를 포착하고, projection 계수의 동역학을 이해하는 데 필요합니다.

• 세부 사항:

  • 미분을 통해 얻은 관계는 projection의 변화량을 설명하며, 일반적으로 이러한 미분은 자기 유사성을 가지는 방정식 형태로 표현됩니다.
  $\frac{d}{dt}c_n(t) = \text{function of } f(t) \text{ and } (c_k(t))_{k \in [N]}$
  • 이 단계는 프로젝션 계수가 시간에 따라 어떻게 변화하는지를 설명하는 ODE(상미분방정식)를 수립하는 데 필수적입니다. 이를 통해, $c(t)$의 동역학이 정량적으로 분석 가능하게 됩니다.

HiPPO 프레임워크

HiPPO는 함수 근사를 위한 일종의 동적 시스템 방법론으로, 주어진 함수 $f(t)$를 시간에 따라 압축하고 저장하는 과정을 다룹니다. 이 과정은 측도에 기반한 직교 기저를 사용하여 함수를 다항식 공간으로 투영(projection)하고, 시간에 따라 변화하는 함수의 정보를 효율적으로 표현할 수 있도록 설계되었습니다.

아래와 그림으로 정리를 하니까 이해가 되는군요! 🔥 (오랜만에 수식보니까 머리가😱)

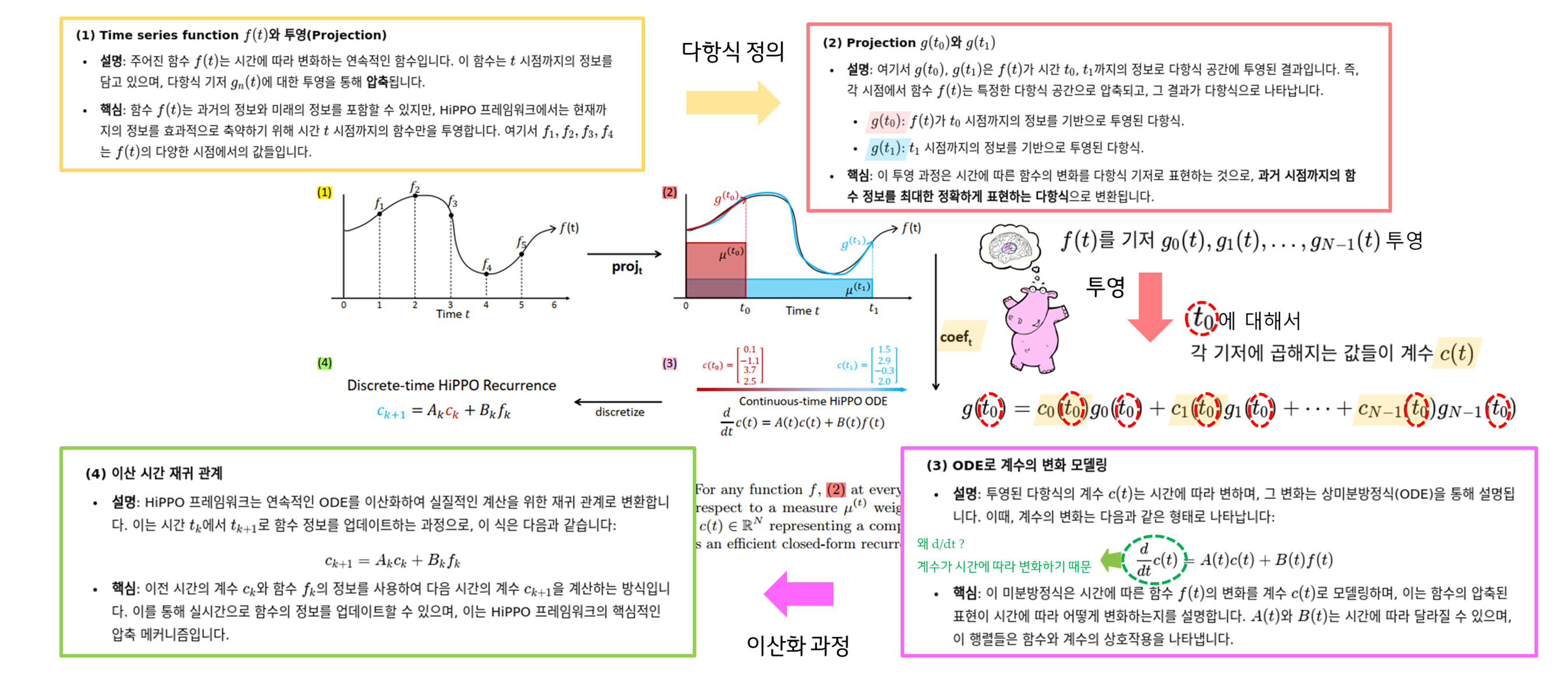
글로 다시 한번 좀 정리해볼까요?

① Projection 연산 : 함수 $f(t)$를 다항식 공간으로 투영

• 투영 연산자 $\text{proj}$는 함수 $f(t)$를 일정 시간 $t$까지의 정보로 제한하여 다항식 공간 $G$에 투영합니다. 즉, 주어진 $f(t)$의 정보를 다항식 $g(t)$로 근사하여 나타냅니다.
• 이 과정에서 중요한 것은, 투영을 통해 얻은 다항식이 시간 $t$ 이전의 함수 정보 $f_{\leq t}(x)$를 최대한 정확하게 표현하는 것입니다. 투영 연산의 목표는, 주어진 측도 $\mu(t)$ 하에서 오차가 최소화되도록 다항식 $g(t)$로 함수를 근사하는 것입니다.

② Coefficients 계산: 계수 $c(t)$ 구하기

• 투영된 다항식 $g(t)$는 다항식 기저 함수들의 선형 결합으로 표현되며, 각 기저 함수에 곱해지는 계수 $c(t)$는 시간에 따라 변화합니다.
• HiPPO는 이 계수 $c(t)$를 효율적으로 계산하여, 함수 $f(t)$의 과거 기록을 압축하는 방식으로 표현합니다. $c(t)$는 $\mathbb{R}^N$의 벡터로, 이는 선택된 $N$개의 기저 함수에 대한 계수를 의미합니다.

③ 미분 방정식 (ODE)으로 계수의 진화 모델링

• 투영된 함수의 계수 $c(t)$는 시간에 따라 진화하며, 이 변화는 상미분 방정식(ODE)으로 표현됩니다:
  $\frac{d}{dt}c(t) = A(t)c(t) + B(t)f(t)$
• 이 방정식은 계수 $c(t)$가 시간 $t$에 따라 어떻게 변화하는지를 설명합니다. $A(t)$와 $B(t)$는 각각 계수와 함수의 변화율을 나타내는 행렬입니다.
• 중요한 점은, HiPPO가 이 ODE를 통해 함수를 시간에 따라 온라인 방식으로 압축한다는 것입니다. 즉, 실시간으로 함수의 정보를 저장하고 진화시킵니다.

💡 High Order Projection: Measure Families and HiPPO ODEs

• HiPPO 프레임워크에서 고차 다항식 투영(High Order Projection)을 통해 과거 데이터를 다항식 형태로 효율적으로 압축하고 이를 실시간으로 업데이트하는 것입니다.
  • 특히, HiPPO에서는 LagT(Translated Laguerre Measure)와 LegT(Translated Legendre Measure) 두 가지 측정(Measure) 방법을 제시하고, 이를 바탕으로 미분 방정식(ODE)을 사용하여 메모리를 업데이트하는 방식을 제안합니다.

💬 Translated Laguerre Measure (LagT)

• LagT는 최근의 데이터가 더 중요하다는 가정을 반영합니다.
  • 과거로 갈수록 데이터의 중요도가 지수적으로 감소합니다.
• Measure 정의:
  $\mu(t)(x) = e^{-(t-x)} \quad \text{(if } x \leq t \text{)}$
  • 이 수식은 $x \leq t$일 때만 정의되며, 과거로 갈수록 $e^{-(t-x)}$라는 함수가 지수적으로 감소함을 나타냅니다.
  • 이는 최근의 데이터가 과거의 데이터보다 중요하다는 의미입니다.
• ODE 형태:
  $\frac{d}{dt} c(t) = -Ac(t) + Bf(t)$
  • 여기서 $c(t)$는 투영된 다항식의 계수 벡터를 의미합니다.
  • 이 식에서 주어진 데이터 $f(t)$는 LagT가 최근 데이터를 중요하게 반영하도록 설계된 방식으로 다항식 기저에 투영됩니다.
• 행렬 A와 B 정의:
  $A_{nk} = \begin{cases} 1 & \text{if } n \geq k \\ 0 & \text{if } n < k \end{cases} \quad, \quad B_n = 1$
  • 이는 지수적 감소를 반영한 메커니즘으로, 최근의 데이터가 더 중요한 방식으로 다항식의 계수들을 업데이트합니다.

💬 Translated Legendre Measure (LegT)

• LegT는 고정된 시간 범위 내의 데이터만 중요하다고 가정합니다.
  • 즉, 일정 길이의 슬라이딩 윈도우(Sliding Window) 방식으로 데이터를 처리합니다.
• Measure 정의:
  $\mu(t)(x) = \frac{1}{\theta} I_{[t-\theta, t]}(x)$
  • 여기서 $I_{[t-\theta, t]}$는 슬라이딩 윈도우를 나타내며, 길이 $\theta$만큼의 시간 창에서 데이터에 균등한 가중치를 부여합니다.
  • 즉, 시간 창 $[t-\theta, t]$ 사이의 데이터를 중요하게 다룹니다.
• ODE 형태:
  $\frac{d}{dt} c(t) = -\frac{1}{\theta} Ac(t) + \frac{1}{\theta} Bf(t)$
  • 여기서도 역시 $c(t)$는 다항식의 계수 벡터를 나타냅니다.
• 행렬 A와 B 정의:
  $A_{nk} = \begin{cases} (-1)^{n-k}(2n + 1) & \text{if } n \geq k \\ 2n + 1 & \text{if } n < k \end{cases} \quad, \quad B_n = (-1)^n (2n + 1)$
  • 이는 일정한 시간 창 내에서 데이터를 투영하여 유지하며, 일정 시간 범위 내의 데이터에만 중요성을 부여합니다.

④ Discrete-time HiPPO Recurrence (이산 시간 재귀 관계)

• HiPPO 프레임워크를 연속 시간(Continuous Time)에서 이산 시간(Discrete Time)으로 변환하는 방법에 대해 설명합니다.

• 이는 실질적인 시계열 데이터나 이산적인 시퀀스 데이터에 적용하기 위해 ODE를 이산화하는 과정입니다.

  • ODE를 이산화하여 실질적으로 계산 가능한 형태로 만들면, 아래와 같은 재귀 관계를 얻게 됩니다:
    $c_{k+1} = A_k c_k + B_k f_k$
  • 이 식은 이전 시간의 계수 $c_k$와 새로운 함수 값 $f_k$을 사용하여 다음 시간 $k+1$에서의 계수 $c_{k+1}$를 계산합니다. 즉, 이 식은 함수의 정보를 이산적인 시간 단계에서 재귀적으로 업데이트하는 방식으로 구현됩니다.
  • 이 과정을 통해, HiPPO는 함수의 과거 기록을 선형 결합의 형태로 압축하여 저장하고, 실시간으로 업데이트하는 효과적인 방법을 제공합니다.

🕐 HiPPO-LegS: Scaled Measures for Timescale Robustness (HiPPO-LegS: 시계열 견고성을 위한 확장된 측정 방법)

• HiPPO-LegS는 시간 척도에 강건한 메모리 메커니즘을 제공하는 새로운 접근 방식입니다. 이 메커니즘은 과거 모든 시간에 대해 균등한 가중치를 부여하여 메모리를 구성합니다.
  
  • 전체 이력 고려: LegS는 완전한 과거 이력을 고려하여 메모리를 구성하며, 이는 특정 슬라이딩 윈도우를 사용하는 기법과 달리 모든 과거 데이터를 균등하게 평가합니다.
    • 반면, LagT와 LegT는 특정 시간 범위 내에서 데이터를 처리하므로 장기적 의존성을 포착하는 데 한계가 있을 수 있습니다.
  • 하이퍼파라미터 필요 없음: LegS는 메모리 구성에 필요한 하이퍼파라미터 없이 동작합니다.
    • 반면, LagT와 LegT는 하이퍼파라미터를 조정해야 할 수 있습니다.
  • 시간 스케일에 대한 강건성: LegS는 입력 신호의 시간 척도가 바뀌어도 안정적으로 동작할 수 있습니다.
    • 반면 LagT나 LegT는 특정 시간 척도에 대해 최적화된 결과를 나타낼 수 있지만, 다른 시간 척도에서는 성능이 저하될 수 있습니다.
  • 시간에 따른 계산 효율성: LegS는 메모리 업데이트 과정을 간소화하여 각 시간 단계에서 더 빠르게 처리할 수 있습니다.
    • LagT나 LegT는 상대적으로 복잡한 업데이트 규칙을 사용해야 할 수 있습니다.
  • Gradient 및 역전파 문제 해결: LegS는 기울기 크기가 보존될 수 있는 메커니즘을 제공하여, 긴 시퀀스에 걸쳐 학습 안정성을 높입니다.
    • LagT와 LegT는 때때로 그래디언트가 소실되는 문제가 발생할 수 있습니다.

---

Empirical Validation (실증적 검증)

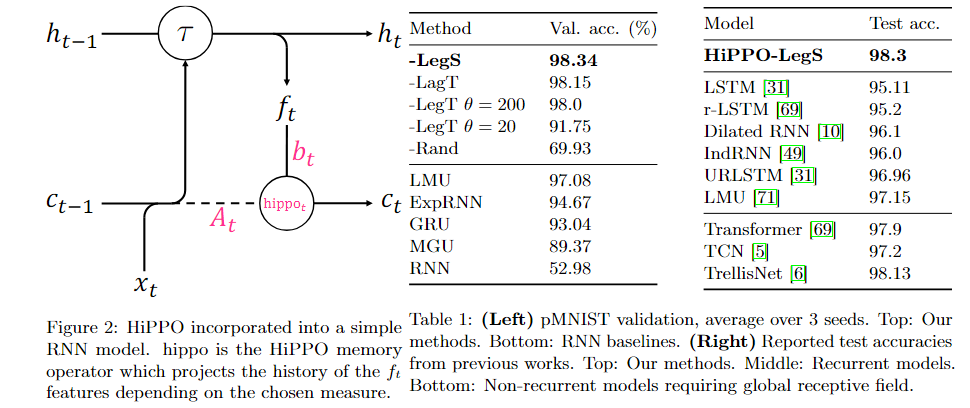
• 4.1 Long-range Memory Benchmark Tasks (장기 메모리 벤치마크 과제): 장기 메모리 의존성을 평가하는 다양한 벤치마크 과제에서 HiPPO-LegS의 성능을 검증합니다.
• 4.2 Timescale Robustness of HiPPO-LegS (HiPPO-LegS의 시계열 견고성): HiPPO-LegS가 다양한 시간 척도에서 얼마나 견고하게 성능을 발휘하는지 검증합니다.
• 4.3 Theoretical Validation and Scalability (이론적 검증 및 확장성): HiPPO 프레임워크가 이론적으로 어떻게 성능이 보장되는지와 그 확장성을 설명합니다.
• 4.4 Additional Experiments (추가 실험): 추가 실험을 통해 HiPPO 메모리 메커니즘의 유용성을 검증합니다.

Conclusion (결론)

• HiPPO 프레임워크가 메모리 문제에 대한 근본적인 해결책을 제시하며, 기존의 메모리 메커니즘을 통합하고 확장하여 더 나은 성능을 발휘할 수 있음을 결론으로 제시합니다

---

2. LSSL: Combining Recurrent, Convolutional, and Continuous-time Models with Linear State-Space Layers (NeurIPS, 2021)

이 논문의 목차에 따른 개념들을 다음과 같이 설명하겠습니다:

Introduction

• LSSL(Linear State-Space Layer)는 순환(Recurrent), 합성곱(Convolutional), 연속 시간 모델(Continuous-time)의 장점을 결합한 새로운 모델 패러다임으로, 시간에 따른 순차 데이터 처리를 더욱 효율적으로 할 수 있도록 설계된 구조입니다.

• 배경 및 문제 정의:

  • 머신러닝에서 시퀀스 데이터(Sequential Data)를 처리하는 일반적인 방식은 RNN(Recurrent Neural Network), CNN(Convolutional Neural Network), NeuralODE(Neural Differential Equation) 등의 구조를 사용하는 것입니다. 이들은 각각 장단점이 있습니다.

    • RNN은 시퀀스 데이터에 대한 상태 저장(Stateful) 성질을 갖고 있으나, 매 스텝마다 저장과 계산이 필요하므로 매우 비효율적입니다. 대표적인 문제로는 Vanishing Gradient Problem이 있습니다.
    • CNN은 병렬 처리와 빠른 훈련이 가능하나, 긴 시퀀스를 처리하는 데 한계가 있습니다. 즉, 로컬 정보에 국한되어 있으며 긴 문맥(long-term dependency)을 기억하는 능력이 부족합니다.
    • NeuralODE는 연속적 시간 모델을 사용하여 수학적으로 시퀀스를 처리하지만 계산 비용이 많이 들고, 특히 긴 시퀀스를 처리할 때 매우 비효율적입니다.

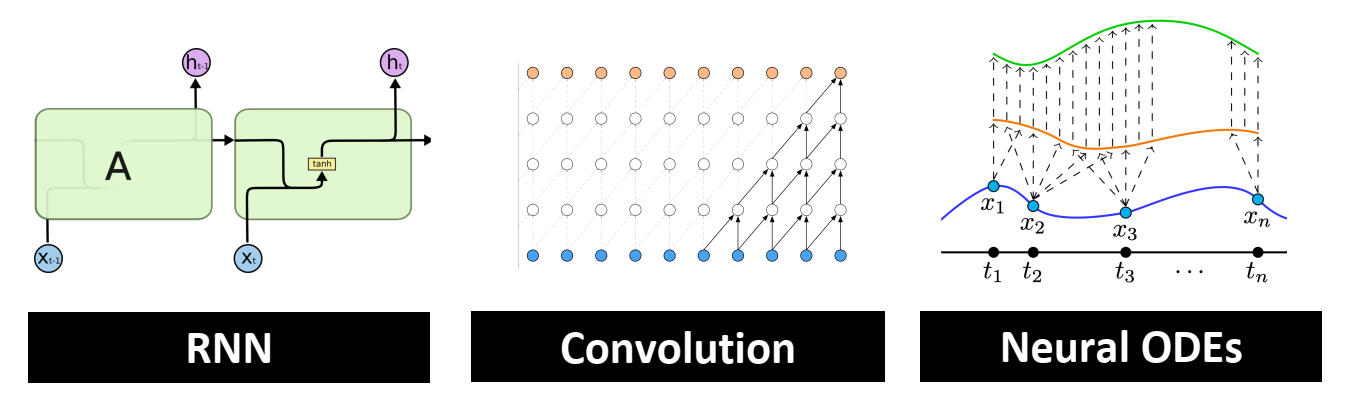
• LSSL의 제안 및 목적:
  • 본 연구에서는 이러한 RNN, CNN, NeuralODE 각각의 장점을 살리면서도 각 모델의 단점을 극복하는 새로운 구조인 Linear State-Space Layer(LSSL)를 제안합니다.
  • 주요 목표는 CNN의 병렬 처리 장점, RNN의 상태 추론 능력, NeuralODE의 시간 척도(Time-scale) 적응력을 동시에 제공하는 모델을 개발하는 것입니다.
    • 재귀성(Recurrent): 특정 시간 간격 $\Delta t$를 사용하여 상태 공간 모델을 불연속화(Discretization)하면, 재귀적인 방식으로 시퀀스를 처리할 수 있습니다. 이를 통해 RNN처럼 상태를 추적할 수 있습니다.
    • 합성곱성(Convolutional): 선형 시간 불변 시스템(Linear Time-Invariant System, LTI)으로서, 연속적인 합성곱으로 표현이 가능합니다. 이를 통해 CNN과 같이 병렬 처리 및 효율적인 훈련이 가능합니다.
    • 연속 시간 모델(Continuous-time): LSSL은 미분 방정식으로 표현되므로 연속 시간 모델로서의 장점을 가지며, 다양한 시간 척도에 적응할 수 있는 유연성을 제공합니다.

아래 그림은 논문에서 나온 Figure1로 위에서 설명하는 LSSL의 3가지 View를 설명합니다.

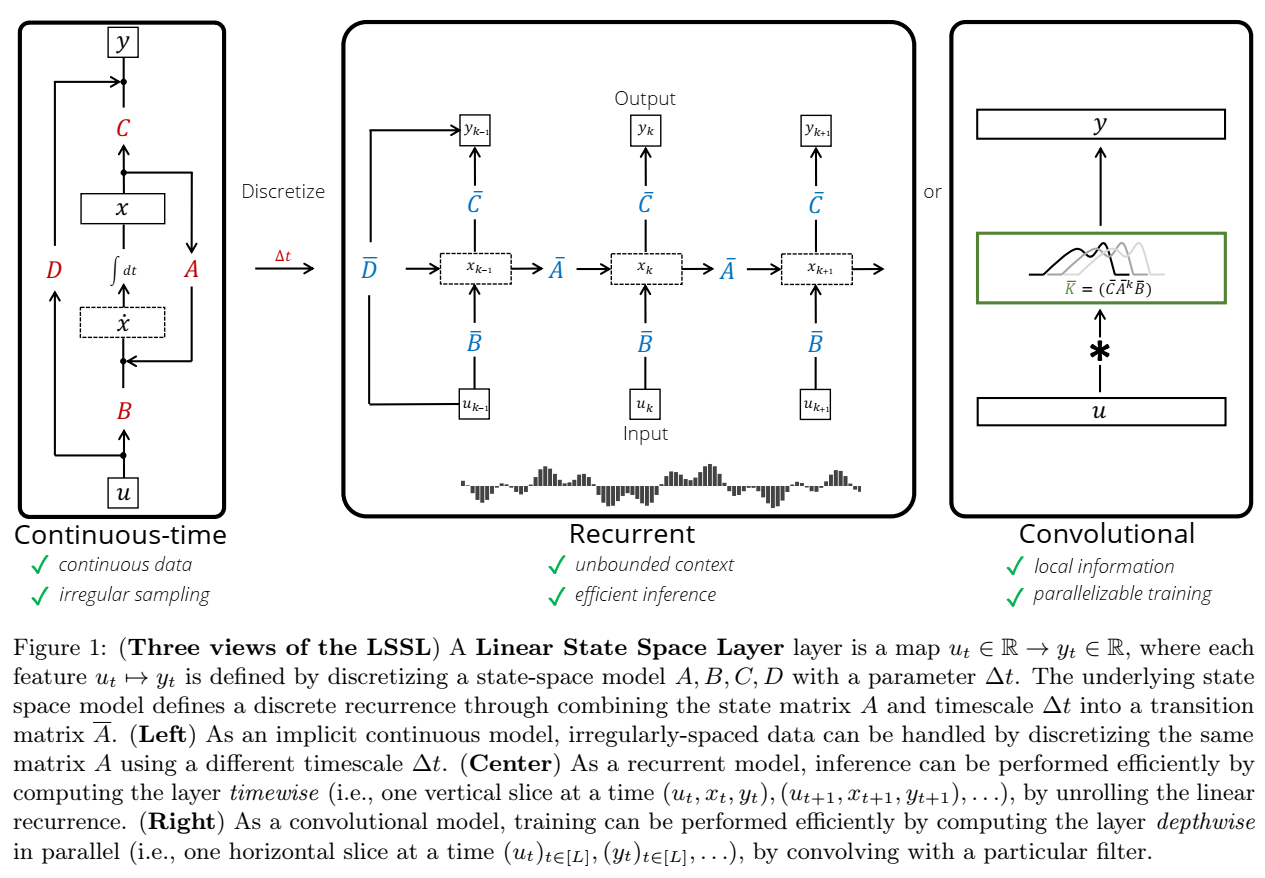
• View 1. Continuous-time 관점:

  • 이 모드에서는 상태 공간 모델이 연속적 시간 $t$에 따라 변하며, 불규칙한 샘플링 데이터도 처리할 수 있습니다. (미분 방정식 형태)
  • 식 $\dot{x}(t) = A x(t) + B u(t)$는 상태가 시간에 따라 어떻게 변화하는지 나타내며, 출력은 $y(t) = C x(t) + D u(t)$로 정의됩니다.

• View 2. Recurrent 관점:

  • 이산화(Discretization)를 통해 RNN과 같은 형태로 사용할 수 있으며 시간 간격 $\Delta t$에 따라 상태가 변화하고, 이전 상태 정보 $x_{k-1}$를 사용하여 현재 상태 $x_k$와 출력을 계산합니다.
  • 이를 통해 무한한 문맥(Unbounded Context)을 처리할 수 있으며, 효율적인 추론이 가능합니다.

• View 3. Convolutional 관점:

  • 합성곱적 방식으로도 표현이 가능합니다. 합성곱 커널 $K$는 선형 시스템을 기반으로 계산되며, 이를 통해 입력 시퀀스에 대해 병렬로 처리할 수 있습니다.
  • CNN과 같이 로컬 정보(Local Information)를 사용하면서도, 병렬화된 훈련이 가능하다는 장점이 있습니다.

Linear State-Space Layers (LSSL)

• 3.1 LSSL의 다양한 뷰 (Different Views of the LSSL)

  • LSSL의 기본 수식은 상태 공간 표현(state-space representation)인 A, B, C, D행렬을 사용하여 정의됩니다. 수식으로는 아래와 같이 표현됩니다.
  $\dot{x}(t) = A x(t) + B u(t)$
  $y(t) = C x(t) + D u(t)$

  • LSSL은 이 모델을 이산화(discretization)하여 $\Delta t$라는 타임스텝을 기반으로 입력 시퀀스 $u(t)$를 출력 시퀀스 $y(t)$로 변환하는 시퀀스 투 시퀀스 맵핑을 제공합니다. 이때, 각 타임스텝의 H-dim feature 벡터를 포함한 시퀀스를 처리합니다.

  • LSSL은 여러 가지 방식으로 계산될 수 있으며, 그 방식들은 크게 재귀적 모델(Recurrent Model), 합성곱 모델(Convolutional Model), 연속 시간 모델(Continuous-Time Model)로 나뉩니다. 논문은 해당 파트에서 이를 도식적으로 표현하면서 각 방식이 어떻게 다르게 작동하는지를 보여줍니다. (이는 앞에의 3. State Space Model(SSM) 소개에서도 다뤘으니 너무 깊게 가지는 않겠습니다)

① Recurrent View (재귀적 관점)

• 재귀적 관점에서는 상태 벡터 $x_{t-1}$이 이전 입력 정보와 현재 입력 정보 간의 문맥을 유지합니다.
  
  • 이를 통해 효율적인 상태 추론을 할 수 있으며, 순환 신경망(RNN)처럼 작동합니다.

② Convolutional View (합성곱 관점)

• 합성곱 관점에서, LSSL은 state 벡터를 통해 필터링된 출력을 제공합니다.
  

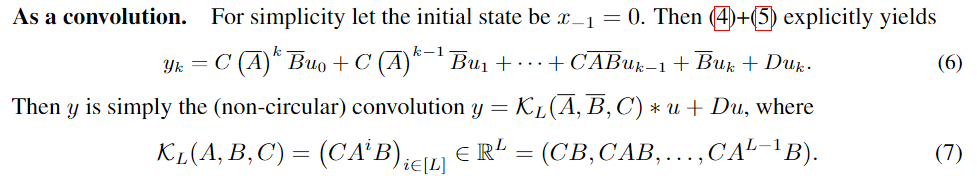
  • 합성곱 관점에서 계산 효율성을 높이기 위해 FFT(빠른 푸리에 변환)를 사용할 수 있습니다.

• 3.2 LSSL의 표현력 (Expressivity of LSSLs)

  • 이 절에서는 LSSL이 실제로 어느 정도까지 다양한 재귀적 특성과 합성곱적 특성 표현을 얼마나 잘 할 수 있는지를 분석합니다.

  ① 합성곱이 가능한 LSSL

  • 상태 공간 시스템과 임펄스 응답(Impulse Response) : 상태 공간 시스템은 기본적으로 연속 시간 또는 불연속 시간 시스템의 입력과 출력을 상태 변수로 표현하는 방식입니다. LSSL도 이러한 상태 공간 시스템을 기반으로 하여 입력 $u(t)$를 시간에 따라 상태 $x(t)$와 출력 $y(t)$로 변환합니다. 수학적으로는 다음과 같은 형태입니다:
  $\dot{x}(t) = A x(t) + B u(t)$
  $y(t) = C x(t) + D u(t)$
  • 여기서 입력 $u(t)$가 주어졌을 때 시스템이 시간에 따라 어떻게 변하는지를 나타내는 함수가 임펄스 응답 함수입니다. 임펄스 응답 함수는 시스템이 특정 입력(즉, 임펄스)에 대해 어떻게 반응하는지를 보여줍니다.

  💬 임펄스 응답 함수(Impulse Response Function, IRF)란 ?

  • 임펄스 응답 함수(IRF)는 시스템이나 신호 처리에서 중요한 개념입니다. 이는 시스템이 단위 임펄스 입력에 대해 어떻게 반응하는지를 나타내는 함수입니다.
  • 임펄스(impulse)는 물리학에서 물체에 작용하는 힘이 시간에 걸쳐 변화하는 과정을 설명하는 개념입니다. 일반적으로 임펄스는 힘과 시간의 곱으로 정의되며, 물체의 운동량 변화와 관련이 있습니다. 수식으로 표현하면 다음과 같습니다: $J = F \cdot \Delta t$

• 임펄스 응답과 합성곱 연산 : 임펄스 응답 함수 $h(t)$는 상태 공간 모델에서 출력을 계산하는데 매우 중요합니다. 임펄스 응답을 알면 입력 신호 $u(t)$가 주어졌을 때 시스템의 출력을 다음과 같은 합성곱 연산으로 표현할 수 있습니다:

  $y(t) = (h * u)(t) = \int h(\tau) u(t - \tau) d\tau$

• 즉, 시스템의 출력은 입력 신호 $u(t)$와 시스템의 임펄스 응답 $h(t)$의 합성곱으로 계산됩니다. 여기서 합성곱 연산이 중요한 이유는, 임펄스 응답 함수가 시스템의 시간적 특성을 결정하며, 이를 통해 과거의 입력들이 현재의 출력을 어떻게 결정하는지를 설명할 수 있기 때문입니다.

• LSSL에서 합성곱의 역할 : LSSL은 상태 공간 시스템을 기반으로 하지만, 이를 이산화(Discretization)하여 합성곱으로 처리할 수 있습니다.

  • 이산화된 시스템은 실제로 시간에 따라 입력이 어떻게 변하는지를 계산할 때, 임펄스 응답 함수를 사용하여 합성곱 필터로 변환할 수 있습니다.
  • 즉, 상태 공간 시스템을 통해 정의된 시스템의 응답을 합성곱 필터로 표현할 수 있다는 의미입니다.

② LSSL의 RNN과의 관계

• RNN은 입력 시퀀스를 처리할 때, 이전 시간의 상태 $h_{t-1}$를 현재 상태 $h_t$에 전달함으로써 시간적 종속성을 유지합니다.

  • 즉, RNN은 이전 타임스텝의 정보를 다음 타임스텝으로 전달하면서 상태를 갱신하고, 이를 통해 긴 시퀀스의 정보를 추적할 수 있습니다. 수학적으로 RNN의 상태 갱신 방정식은 다음과 같이 표현됩니다:
    $h_t = \sigma(W_h h_{t-1} + W_x x_t)$
  • LSSL도 RNN처럼 시간에 따른 상태 갱신을 수행합니다. LSSL의 상태 갱신 방정식은 상태 공간 모델에 기반한 미분 방정식으로 정의되는데, 이를 이산화하면 RNN과 유사한 구조가 됩니다.

  $h'(t) = Ah(t) + Bx(t)$
  $y(t) = Ch(t) + Dx(t)$
  ↓ 이산화 수행
  $h_{k+1} = \bar{A}h_k + \bar{B}x_k$
  $y_k = Ch_k + Dx_k$

  • 또한, RNN은 위와 같은 상태 갱신 과정에서 게이팅 메커니즘(Gating Mechanism)을 통해 각 타임스텝에서 정보를 얼마나 전달할지 조절합니다. LSTM이나 GRU에서의 게이팅 메커니즘은 RNN이 각 타임스텝에서 정보의 흐름을 조절하는 중요한 요소입니다.

  • 이 게이팅 메커니즘은 사실상 시간 척도(Time-scale)를 부드럽게 하여 각 스텝에서의 상태 변화가 너무 급격하지 않게 만드는 역할을 합니다. 예를 들어, LSTM의 Forget Gate는 이전 상태를 얼마나 기억할지 조절하는데, 이는 일정한 시간 척도에서의 변화를 부드럽게 하는 역할을 합니다.
    

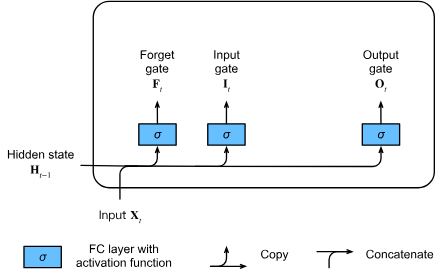
  • LSSL에서도 $\Delta t$라는 시간 간격(Time-step)이 중요한 역할을 합니다. 이 시간 간격은 각 타임스텝 간의 상태 변화를 결정하며, 이는 RNN에서 게이팅 메커니즘과 매우 유사한 역할을 합니다.

    • 즉, LSSL의 시간 척도는 RNN의 게이팅 메커니즘과 본질적으로 같은 개념으로, 입력 데이터를 처리할 때 시간에 따른 변화량을 부드럽게 조절하는 역할을 합니다.

③ Deep LSSL

• LSSL을 하나의 레이어로 사용하지 않고 여러 레이어로 쌓아서 보다 깊은 네트워크로 확장할 수 있습니다. 이 구조는 특히 비선형 시퀀스 데이터를 처리하는 데 적합합니다.

  • 기본 LSSL 구조 : LSSL은 $\mathbb{R}^L \to \mathbb{R}^L$ seq-to-seq 매핑을 수행하며, 각각의 LSSL 레이어는 파라미터 $A, B, C, D$와 시간 간격 $\Delta t$로 정의됩니다. 입력 시퀀스는 H 차원의 피처로 처리되며, 각 피처가 독립적으로 학습됩니다.

  • Layer Stacking : Deep LSSL은 여러 LSSL 레이어를 쌓아서 더 복잡한 시퀀스 데이터를 처리할 수 있습니다. 각 레이어는 서로 다른 상태 공간 파라미터와 시간 간격을 학습하여, 다차원적인 시간 척도에서 데이터를 처리합니다.

  • Residual Connections : ResNet과 같은 Residual Connections을 사용하여 딥러닝 네트워크에서 발생할 수 있는 기울기 소실 문제를 해결합니다. 각 레이어의 출력을 다음 레이어로 직접 전달함으로써 정보가 사라지지 않게 유지하는 방식입니다.

  • Normalization : LSSL의 레이어가 깊어질수록 Layer Normalization이 필요합니다. 이는 레이어가 쌓일 때 발생하는 내부 공변량 변화(Internal Covariate Shift)를 줄여주어, 학습 속도를 높이고 성능을 개선합니다.

Appendix B.1 (M) LSSL Computation

• LSSL의 계산은 시간이 많이 걸릴 수 있지만, 일부 계산을 캐싱함으로써 효율성을 높일 수 있습니다. 특히, 훈련되지 않은 $A$와 $\Delta t$ 파라미터를 고정할 경우 캐싱을 통해 계산 효율을 극대화할 수 있습니다.
  • 전이 행렬(Transition Matrix): 상태 전이 행렬 $\bar{A}$는 블랙박스 매트릭스-벡터 곱 알고리즘을 사용하여 계산되며, 이를 캐싱해 둠으로써 연산을 반복하지 않아도 됩니다.
  • 크릴로프 행렬(Krylov Matrix): 크릴로프 행렬은 입력과 상태 전이 행렬 $A$, 그리고 $B$ 행렬을 통해 계산되며, 이 계산은 병렬화될 수 있습니다. 제곱 연산 및 지수화를 통해 효율적으로 계산할 수 있습니다. 최종적으로 이 크릴로프 행렬은 $(A^k B)$의 형태로 캐싱되어 합성곱 연산 전에 저장됩니다.
  • 복잡도: 캐싱을 사용한 이 알고리즘은 계산 복잡도가 $O(NL)$로 줄어들지만, 이를 캐싱하기 위한 추가적인 메모리 공간이 필요합니다. 이 부분은 훈련 시 모델의 효율성을 극대화할 수 있지만, inference 시에는 더 많은 계산이 요구될 수 있습니다.

Appendix B.2 Initialization of $A$

• 파라미터 $A$는 HiPPO-LegS 연산자를 사용하여 초기화됩니다. HiPPO-LegS는 연속 시간 메모리화 문제를 해결하기 위해 설계된 연산자로, 상태 공간 시스템에서 긴 시퀀스 데이터를 효율적으로 처리하는 데 도움을 줍니다.
• $A$는 특정 규칙에 따라 대각 행렬을 구성하는데, $A$의 초기값은 아래와 같이 주어집니다:
  $A_{nk} = \begin{cases} (2n + 1)^{1/2}/(2k + 1)^{1/2} & \text{if } n \geq k \\ n + 1 & \text{if } n = k \\ 0 & \text{if } n < k \end{cases}$
• 이 초기화 방식은 LSSL의 상태 전이가 HiPPO 연산에 맞추어 최적화되도록 하며, 긴 시퀀스 메모리화 문제를 해결하는 데 도움을 줍니다.

Appendix B.3 Initialization of $\Delta t$

• LSSL에서 $\Delta t$는 각 레이어에서 상태 공간 시스템의 시간 간격(Time-step)을 조절하는 중요한 파라미터입니다. $\Delta t$는 로그 균등 분포(log-uniform distribution)를 사용하여 초기화되며, 이는 시간 척도 $\Delta t$를 다양하게 설정함으로써 여러 시간 척도를 학습할 수 있도록 합니다.
  • 최소 시간 간격 $\Delta t_{min}$와 최대 시간 간격 $\Delta t_{max}$를 설정하여, 데이터의 시퀀스 길이에 맞게 시간 간격을 초기화합니다.
  • 이 파라미터는 시퀀스 데이터의 길이와 데이터셋마다 다르게 설정될 수 있으며, 다양한 시간 척도에 대해 모델이 적응할 수 있게 합니다.

Combining LSSLs with Continuous-time Memorization
기본 LSSL은 긴 시퀀스를 처리하는 데 있어 두 가지 문제가 있었습니다: (1) 기울기 소실 문제와 (2) 연산 복잡도 문제

• 4.1 Incorporating Long Dependencies into LSSLs (기울기 소실 문제):
  • 문제: 상태 전이 행렬 $A$를 무작위로 설정하거나 적절하게 설계하지 않으면, 긴 시퀀스를 처리할 때 기울기 소실 문제가 발생합니다. 이는 네트워크가 긴 시간 동안 중요한 정보를 유지하지 못하는 문제로, 특히 LSSL이 RNN과 같은 순환 구조를 가지고 있기 때문에 발생할 수 있습니다.
    • LSSL은 긴 시퀀스 데이터를 처리할 수 있는 구조를 갖추고 있지만, 무작위(random initialized) 상태 행렬 $A$를 사용할 경우 효과가 크지 않음을 경험적으로 확인하였습니다. (실험적으로 확인함)
  • 해결책: 이를 해결하기 위해 HiPPO 프레임워크를 적용하여, 적절한 상태 전이 행렬 $A$를 설계합니다. HiPPO는 시간에 따른 중요한 정보를 잘 유지할 수 있도록 상태 공간 모델을 최적화하여 기울기 소실 문제를 완화합니다.
• 4.2 Theoretically Efficient Algorithms for the LSSL (연산 복잡도 문제):
  • 문제: LSSL은 상태 전이 행렬 $A$와 벡터의 곱셈(Matrix-Vector Multiplication, MVM)이나 Krylov 공간에서의 합성곱 연산이 포함되는데, 이 연산들이 매우 복잡하고 시간이 많이 걸릴 수 있습니다. 특히, 긴 시퀀스를 처리할 때 연산 복잡도가 커지는 문제가 있습니다.
  • 해결책: 이를 해결하기 위해 Quasiseparable 행렬을 사용하여, 상태 전이 행렬의 특성을 활용한 효율적인 계산 방법을 제안합니다. Quasiseparable 행렬은 선형 시간 복잡도로 계산할 수 있으며, Krylov 공간에서의 연산을 더 빠르고 효율적으로 수행할 수 있게 해줍니다.

Empirical Evaluation

• 5.1 Image and Time Series Benchmarks: 시계열 이미지와 같은 데이터셋에서 LSSL의 성능을 평가한 실험 결과를 설명합니다. 여기에는 sMNIST, pMNIST, sCIFAR와 같은 유명한 벤치마크에서의 성능 비교가 포함됩니다.
• 5.2 Speech and Image Classification for Very Long Time Series: 매우 긴 시퀀스 데이터를 처리하는 음성 및 이미지 분류 문제에서 LSSL이 기존 모델보다 뛰어난 성능을 보였다는 점을 설명합니다.
• 5.3 Advantages of Recurrent, Convolutional, and Continuous-time Models: 재귀적, 컨볼루션, 연속-시간 모델의 장점을 모두 갖춘 LSSL의 장점을 강조합니다.
• 5.4 LSSL Ablations: Learning the Memory Dynamics and Timescale: LSSL이 시퀀스의 시간 스케일을 자동으로 학습할 수 있는 능력을 분석하고, 메모리 동력학을 학습하는 방법에 대한 실험 결과를 보여줍니다.

---

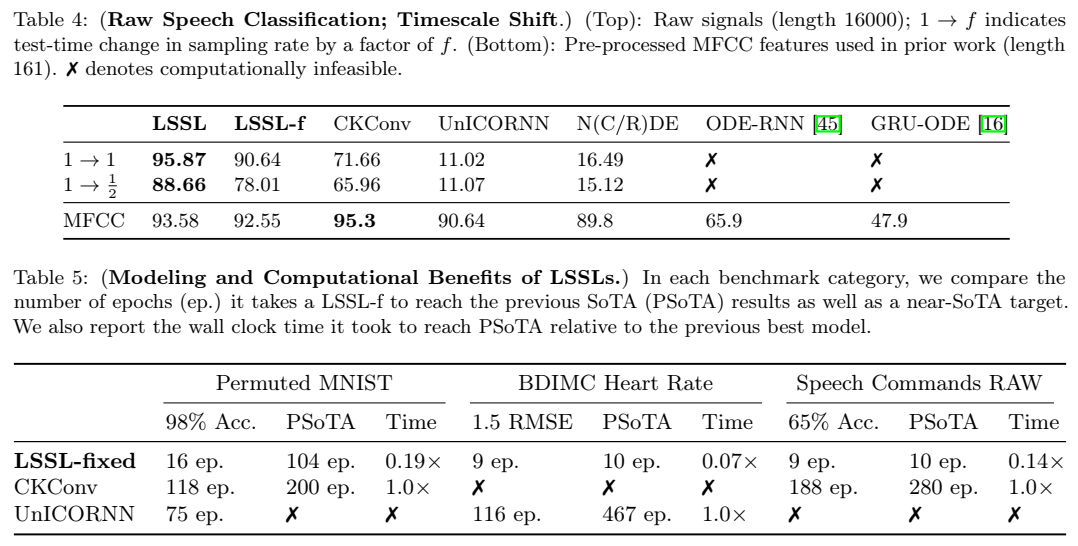
3. S4: Efficiently Modeling Long Sequences with Structured State Spaces (ICLR, 2022)

Introduction

• 이 섹션에서는 순차 데이터(sequence data) 모델링의 주요 과제인 장기 종속성(long-range dependencies) 문제를 다루며 기존의 모델(RNN, CNN, Transformer 등)이 긴 시퀀스를 처리하는 데 있어 겪는 문제점을 제시합니다.

  • RNNs (Recurrent Neural Networks): RNN 계열 모델은 본래 순차 데이터 처리를 위해 개발되었으나, vanishing gradient(기울기 소실) 문제로 인해 긴 시퀀스를 처리하는 데 한계가 있습니다.
  • CNNs (Convolutional Neural Networks): CNN은 시퀀스 길이를 확장하기 위해 dilated convolutions(확장된 컨볼루션) 등을 도입했으나 여전히 긴 시퀀스 처리에서 성능이 저하됩니다.
  • Transformers: Transformers 모델은 대규모 시퀀스 처리에 널리 사용되지만, quadratic scaling(시퀀스 길이에 따른 연산 복잡도가 제곱에 비례) 문제로 인해 매우 긴 시퀀스에서는 비효율적입니다.

• 대안적 접근법으로 최근 연구에서는 상태 공간 모델(SSM)을 기반으로 한 접근법이 제안되었습니다. SSM은 제어 이론 등 다양한 분야에서 오래전부터 사용되어 온 모델로 시간에 따라 변화하는 상태를 표현하고, 이를 통해 장기적인 시계열 데이터를 처리할 수 있습니다. 그러나 기존 SSM을 딥러닝에 적용하는 데는 계산 비용과 메모리 사용량이 매우 크다는 한계에 봉착했습니다.

• 본 논문에서는 이러한 문제를 해결하기 위해 S4(Structured State Spaces) 모델을 제안합니다. 이 모델은 상태 공간 모델의 수학적 강점을 유지하면서도, 이를 더 효율적으로 계산할 수 있는 방법을 제공합니다.

  • S4는 상태 행렬 A를 저랭크(low-rank)와 정규 행렬(normal matrix)로 분해하여 계산의 안정성과 효율성을 높입니다.
  • 특히 S4는 Cauchy kernel을 사용하여 효율적인 계산을 가능하게 하며, 이로 인해 긴 시퀀스를 처리하는 데 필요한 연산량과 메모리 사용량을 크게 줄일 수 있습니다.

• Figure 1 설명

  

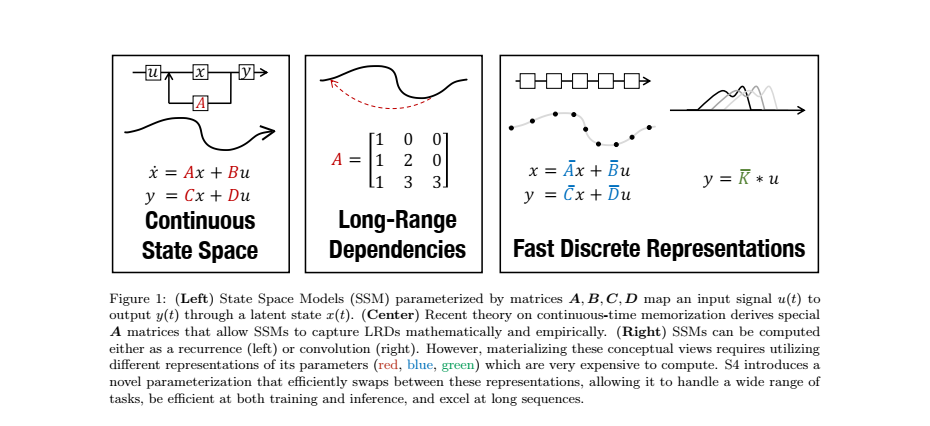
  1. (왼쪽) 상태 공간 모델: 상태 공간 모델은 입력 신호 $u(t)$가 주어졌을 때, 이를 은닉 상태 $x(t)$로 변환한 뒤, 최종적으로 출력 $y(t)$를 생성하는 시스템입니다.

     • 상태 변환은 상태 행렬 $A$, 입력 행렬 $B$, 출력 행렬 $C$, 그리고 스킵 연결을 담당하는 행렬 $D$에 의해 정의됩니다.
     • 이 모델은 제어 이론과 계산 신경과학에서 광범위하게 사용되며, 특히 연속 시간 시스템을 모델링하는 데 적합합니다.

  2. (중앙) 연속 시간 메모리 이론: 최근 연구에서는 특정 행렬 $A$를 사용하면 SSM이 장기 종속성(Long-Range Dependencies, LRDs)을 수학적으로나 실험적으로 효과적으로 처리할 수 있음을 입증했습니다. (이전 연구)

     • 이러한 행렬은 HiPPO라는 이론에서 유도된 특별한 행렬로, 입력의 긴 이력을 기억하는 데 최적화되어 있습니다.

  3. (오른쪽) 재귀 및 컨볼루션 표현: SSM은 두 가지 방식으로 계산할 수 있습니다. 재귀적 방식과 컨볼루션 방식.

     • 재귀적 방식은 RNN처럼 순차적으로 계산되며, 컨볼루션 방식은 병렬화가 가능해 더 빠른 연산이 가능합니다.
     • S4는 이러한 서로 다른 표현 간의 변환을 효율적으로 수행할 수 있도록 설계되었으며, 다양한 작업에 적합한 방식으로 효율적인 학습과 추론을 지원합니다.

Method: Structured State Spaces (S4)

• 3.1 동기: 대각화 (Motivation: Diagonalization)

  • 문제 정의 : 상태 공간 모델(SSM)의 중요한 문제는, 상태 공간의 크기가 커짐에 따라 연산 복잡도가 증가한다는 것입니다. 구체적으로, HiPPO 행렬 $A$를 여러 번 곱하는 연산이 복잡도를 증가시키는 주 원인입니다. (∵상태 업데이트를 위해서는 A를 여러번 곱해야함)
    • 상태 공간 모델에서 $A$는 상태 갱신을 담당하는 핵심 행렬이며, 이를 사용하는 연산은 반복적으로 일어납니다. $A$를 직접 계산하면 $O(N^2L)$에 달하는 연산량과 $O(NL)$의 메모리 공간이 필요합니다. 이는 특히 대규모 시퀀스 모델링에서 병목이 됩니다.
      이를 해결하기 위해, 켤레(conjugation)라는 수학적 기법을 도입하여 연산을 단순화할 수 있습니다.

• Lemma 3.1: 켤레 관계 : 이 레마에서는 상태 공간 모델(SSM)의 행렬 $A$, $B$, $C$에 켤레 변환 을 적용하면 동일한 모델을 얻을 수 있음을 보여줍니다. 이 말은, 두 상태 공간 모델이 서로 동일한 정보를 표현하고 있지만 다른 좌표계에서 표현될 수 있다는 의미입니다. 이를 통해 시스템의 복잡한 계산을 더 단순화할 수 있습니다.

  켤레 변환이란?

  • 선형대수학에서 켤레 변환(conjugate transformation)은 복소수 행렬이나 벡터에 적용되는 중요한 연산입니다. 이 변환은 복소수 행렬에 대해 두 가지 연산을 순차적으로 수행합니다: ① 행렬을 전치(transpose)합니다. ② 각 원소를 켤레 복소수로 변환합니다

  켤레 변환의 의의

  • 시스템 분석: 켤레 변환을 통해 시스템을 더 쉽게 분석할 수 있는 형태로 변환할 수 있습니다.
    • 예를 들어, 대각화나 정규형으로의 변환이 가능합니다.
  • 제어 설계: 상태 피드백 제어나 관측기 설계 시, 켤레 변환을 통해 더 간단한 형태의 시스템으로 변환하여 설계를 수행할 수 있습니다.
  • 계산 효율: 특정 형태로의 변환을 통해 계산 효율을 높일 수 있습니다. 예를 들어, 대각 행렬은 계산이 매우 간단합니다.

  켤레 관계의 의미 : 켤레 관계는 주로 복소수나 행렬에서 사용되는 개념입니다.

  • 복소수에서의 켤레 : 복소수 a + bi의 켤레는 a - bi입니다. 켤레 복소수는 실수부는 같고 허수부의 부호만 반대입니다.
  • 행렬에서의 켤레 전치 : 행렬 A의 켤레 전치(conjugate transpose)는 A*로 표기하며, 행렬을 전치한 후 각 원소를 켤레 복소수로 바꾼 것입니다

  

  • 두 개의 상태 공간 모델을 생각해 봅시다. 하나는 원래의 상태 벡터 $x$를 사용하고, 다른 하나는 변환된 상태 벡터 $\tilde{x} = Vx$를 사용합니다. 여기서 $V$는 변환을 수행하는 행렬입니다.

    • 각각의 상태 공간 방정식은 다음과 같습니다.

      1. 원래 상태 공간 모델:

         $x' = Ax + Bu$
         $y = Cx$

      2. 변환된 상태 공간 모델:

         $\tilde{x}' = V^{-1}AV\tilde{x} + V^{-1}Bu$
         $y = CV\tilde{x}$

  • 이 두 모델은 동일한 시스템을 나타내며, 이는 켤레 변환 이 상태 공간 모델에서 동등 관계임을 의미합니다. 이를 통해 우리는 $A$, $B$, $C$ 행렬을 변환하여 동일한 연산을 다른 형태로 계산할 수 있게 됩니다. 켤레 관계는 아래 식으로 정의됩니다.

    $(A, B, C) \sim (V^{-1} A V, V^{-1} B, C V)$

  • 즉, 행렬 $V$를 사용하여 상태 벡터 $x$를 변환하면, 새로운 상태 벡터 $\tilde{x} = Vx$로 변환된 시스템에서 더 효율적인 연산이 가능합니다.

  • 행렬 $A$를 $V^{-1} A V$로 변환하여 대각화하면, $A$가 대각 행렬일 때 계산이 단순해집니다.

• Lemma 3.2: HiPPO 행렬의 대각화: 이 레마는 HiPPO 행렬 $A$가 대각화될 수 있음을 보여줍니다. 여기서 대각화는 복잡한 행렬 연산을 더 단순하게 만들어주는 중요한 수학적 기법입니다.
  

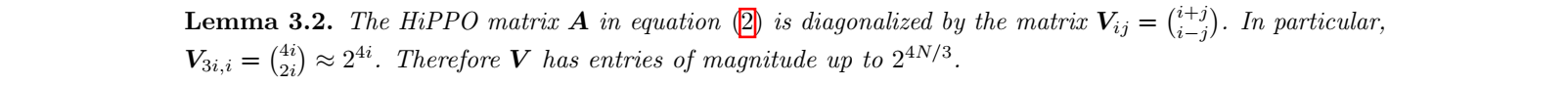
  • HiPPO 행렬은 시계열 데이터를 처리하기 위한 특정 유형의 행렬인데, 이 행렬의 대각화는 계산 효율성을 높이는 데 중요한 역할을 합니다.

  • HiPPO 행렬 $A$는 대각화될 수 있으며, 대각화에 사용되는 변환 행렬 $V$와 행렬 $V$의 각 항목 $V_{3k,i}$는 아래와 같이 정의됩니다.

    $V_{ij} = \left( \binom{i+j}{i-j} \right)$
    $V_{3k,i} = \left(\binom{k}{i}\right) 2^{i-k}$

  • 이 식을 통해, $V$의 항목은 $2^{iN/3}$ 정도의 크기를 가집니다. 이 수식을 통해 HiPPO 행렬을 대각화하여 연산을 간소화할 수 있습니다.

• 3.2 S4 파라미터화: Normal Plus Low-Rank Parameterization (NLPR)

  • 기본적인 HiPPO 행렬 $A$는 대각 행렬이 아니며, 일반적으로 계산이 복잡합니다. 이를 해결하기 위해, 논문에서는 정규 행렬(normal matrix)과 저랭크 행렬(low-rank matrix)의 합으로 분해하는 기법을 제시합니다.

  정규 행렬 (Normal Matrix) : 정규 행렬은 특별한 성질을 가진 정사각 행렬입니다.

  • 정의: 행렬을 뒤집고 복소수 부분의 부호를 바꾼 것(켤레 전치)과 원래 행렬을 곱했을 때, 순서를 바꿔도 같은 결과가 나오는 행렬입니다.

  저랭크 행렬 (Low-rank Matrix) : 저랭크 행렬은 복잡한 정보를 간단하게 표현할 수 있는 행렬입니다.

  • 정의: 행렬의 랭크(독립적인 행 또는 열의 수)가 작은 행렬을 말합니다.

  • 정규 행렬은 대각화가 가능하지만, HiPPO 행렬 자체는 이 속성을 만족하지 않으므로 이를 활용할 수 없습니다.

  • 대신, HiPPO 행렬은 정규 행렬과 저랭크 행렬의 합으로 근사할 수 있습니다. 즉, $A$는 아래와 같이 분해됩니다.

    $A = V \Lambda V^{-1} - PQ^T$
    • $\Lambda$: 대각 행렬
    • $P$, $Q$: 저랭크 행렬

  • 저랭크 행렬의 항목 수가 적기 때문에 계산이 효율적으로 이루어질 수 있으며, 이러한 분해는 NPLR (Normal Plus Low-Rank) 기법으로 알려져 있습니다. 이 방법을 사용하면, $A$를 여러 번 곱하는 연산의 복잡도를 대폭 줄일 수 있다고 합니다.

  • (Theorem 1) 모든 HiPPO 행렬의 NPLR 표현 : 모든 HiPPO 행렬이 NPLR 표현을 가질 수 있음을 증명합니다. 이를 통해, S4 모델에서 사용되는 행렬 $A$는 아래와 같이 표현됩니다.
    

    $A = V\Lambda V^{-1} - PQ^T = V\left(\Lambda - (V^{-1}P)(V^{-1}Q)^T\right)V^{-1}$
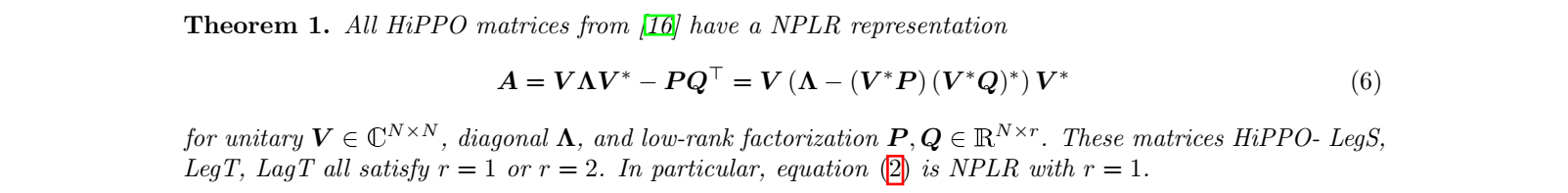
    • $\Lambda$는 대각 행렬
    • $P$와 $Q$는 저랭크 행렬

• 3.3 S4 Algorithms and Computational Complexity : 이 섹션에서는 S4 모델에서 제안하는 주요 알고리즘과 그 복잡도에 대해 설명합니다. 정리 2 와 정리 3 은 각각 재귀 연산과 컨볼루션 연산의 복잡도를 다룹니다.
  

  • Theorem 2: S4 Recurrence에서는 재귀 연산의 복잡도를 $O(N)$으로 줄일 수 있음을 설명합니다. 재귀 연산은 상태 공간 모델에서 중요한 연산이며, 이를 효율적으로 수행하는 방법을 제안합니다.

  • Theorem 3: S4 Convolution에서는 SSM의 컨볼루션 필터 $K$를 계산하는 연산을 $O(N + L)$로 줄일 수 있음을 설명합니다. 이 필터는 시퀀스 모델에서 주로 사용되는 핵심 연산 중 하나입니다.

    • 컨볼루션 필터의 계산은 4개의 케우시 곱셈(Cauchy multiplies)으로 이루어지며, $O(N + L)$ 연산만 필요합니다. 이로 인해 S4 모델은 대규모 시퀀스 데이터를 처리하는 데 매우 효율적입니다.

    케우시 행렬(Cauchy Matrix): 두 벡터의 원소 차이의 역수로 이루어진 특수한 행렬.

    $C_{ij} = \frac{1}{x_i - y_j}$

    케우시 곱셈(Cauchy Multiplication): 함수나 수열의 곱셈을 효율적으로 계산하는 방법으로, 다항식의 곱이나 컨볼루션 연산에서 사용됨.

Algorithm 1: S4 Convolution Kernel

• 알고리즘 1은 S4 컨볼루션 커널(S4 Convolution Kernel)을 계산하는 절차를 설명하고 있습니다. 이 알고리즘은 상태 공간 모델(SSM)을 기반으로 시퀀스 데이터에서 컨볼루션 필터를 효율적으로 계산하는 방법을 제시합니다. 아래 그림을 기준으로 설명합니다.

입력

• $\Lambda, P, Q, B, C$: 상태 공간 모델에서 상태 업데이트, 입력 및 출력에 관련된 S4 모델의 파라미터.
• $\Delta$: 시간 간격 또는 단계 크기(step size).

출력

• $K$: S4 모델의 컨볼루션 커널 (SSM 최종 컨볼루션 필터)

단계별 설명

• ① SSM 생성 함수 $\tilde{C}$ 계산

  • 여기서, SSM 생성 함수(Generating Function) $\tilde{C}$는 아래와 같이 정의됩니다.

    $\tilde{C} \leftarrow \left( I - A^L \right)^{-1} C$

  • $A^L$는 행렬 $A$를 시간 단계 $L$에 대해 제곱한 행렬을 의미합니다.

    • 이 연산은 상태 공간 모델에서 상태 갱신을 나타내며, $C$와 결합하여 상태 공간의 출력을 계산할 수 있습니다. (참고로, C는 상태 공간 모델(SSM)의 출력 행렬)

  • $I - A^L$은 단위 행렬 $I$에서 행렬 $A^L$을 뺀 것입니다. 이는 $A$가 시스템에 미치는 영향을 반영하여 단위 행렬에서 일정 부분을 조정하는 역할을 합니다.

  • $(I - A^L)^{-1}$은 상태 공간 모델에서 여러 시간 스텝에 걸친 상태 변화를 고려합니다. 이를 통해 시스템의 현재 상태에 대한 정보를 추출하고, 시간이 지남에 따라 상태가 어떻게 변화하는지 계산한 후, 그 영향을 역으로 계산하는 역할을 합니다.

  • 이 단계에서 최종적으로 $\tilde{C}$를 계산하여 SSM을 나타내는 벡터를 얻습니다. 이를 통해 생성된 상태 벡터는 이후의 컨볼루션 커널 계산에 사용됩니다.

• ② SSM 케우시 곱셈 (Cauchy Multiplication)

  • $K$의 각 성분을 아래와 같이 케우시 곱셈을 통해 계산합니다.

    $\begin{bmatrix} k_{00}(\omega) & k_{01}(\omega) \\ k_{10}(\omega) & k_{11}(\omega) \end{bmatrix} \leftarrow \tilde{C} \cdot \left[ \left( \Delta \frac{1 - \omega}{1 + \omega} - \Lambda \right)^{-1} \cdot B P \right]$

  • 여기서 케우시 곱셈(Cauchy Multiplication)을 사용하여 복잡한 행렬 연산을 효율적으로 수행합니다. Cauchy 행렬은 특수한 형태의 행렬로, 여기에서는 $P$와 $B$ 행렬을 곱하여 최종 컨볼루션 필터 $K$를 계산하는 데 사용됩니다.

  • $\Lambda$는 대각 행렬이고, $B$와 $P$는 S4 모델에서 상태와 입력에 대한 저랭크 행렬입니다.

• ③ Woodbury Identity 적용

  • Woodbury Identity는 대규모 행렬의 역행렬을 계산할 때 사용하는 효율적인 방법입니다. 이를 적용하여 컨볼루션 필터의 계산을 더욱 간소화할 수 있습니다.

  • Woodbury Identity는 저랭크 행렬을 포함하는 역행렬을 빠르게 계산할 수 있게 해주며, $A + PQ^*$ 형태의 행렬을 $A^{-1}$로 바꿔줍니다. 이로 인해 행렬 연산이 대폭 단순해집니다.

• ④ $\tilde{K}(\omega)$ Evaluate(평가)

  • $K(\omega)$는 모든 근(roots of unity) $\omega \in \Omega_L$에서 평가됩니다.

    $\tilde{K}(\omega) \leftarrow \frac{2}{1 + \omega} \left[ k_{00}(\omega) - k_{01}(\omega)(1 + k_{11}(\omega))^{-1}k_{10}(\omega) \right]$

  • 이 단계에서 각 필터의 요소가 근을 통해 평가되고, 이를 통해 필터의 각 주파수 성분이 계산됩니다. (계산과정 아래 참고)

    1. $\omega$ 설정: $L$개의 단위 근 $\omega_k$를 계산합니다.

       $\omega_k = e^{-2\pi i k / L}, \quad k = 0, 1, \dots, L-1$

    2. $K(\omega_k)$ 계산: 각 $\omega_k$에 대해 $K(\omega_k)$를 계산합니다. 이는 필터의 주파수 응답을 나타냅니다.

       $\tilde{K}(\omega_k) \leftarrow \frac{2}{1 + \omega_k} \left[ k_{00}(\omega_k) - k_{01}(\omega_k)(1 + k_{11}(\omega_k))^{-1}k_{10}(\omega_k) \right]$

    3. 주파수 도메인에서의 연산: 계산된 $K(\omega_k)$를 사용하여 입력 신호의 주파수 성분과 곱셈을 수행합니다.

• ⑤ 역 FFT(Inverse FFT) 적용

  • 마지막 단계에서 역 Fourier 변환(iFFT)을 사용하여 필터의 주파수 도메인 표현을 시간 도메인으로 변환합니다. 이 과정에서 최종적인 컨볼루션 커널 $K$가 계산됩니다.
    $K \leftarrow \text{IFFT}(\tilde{K}(\omega_k))$

Experiments

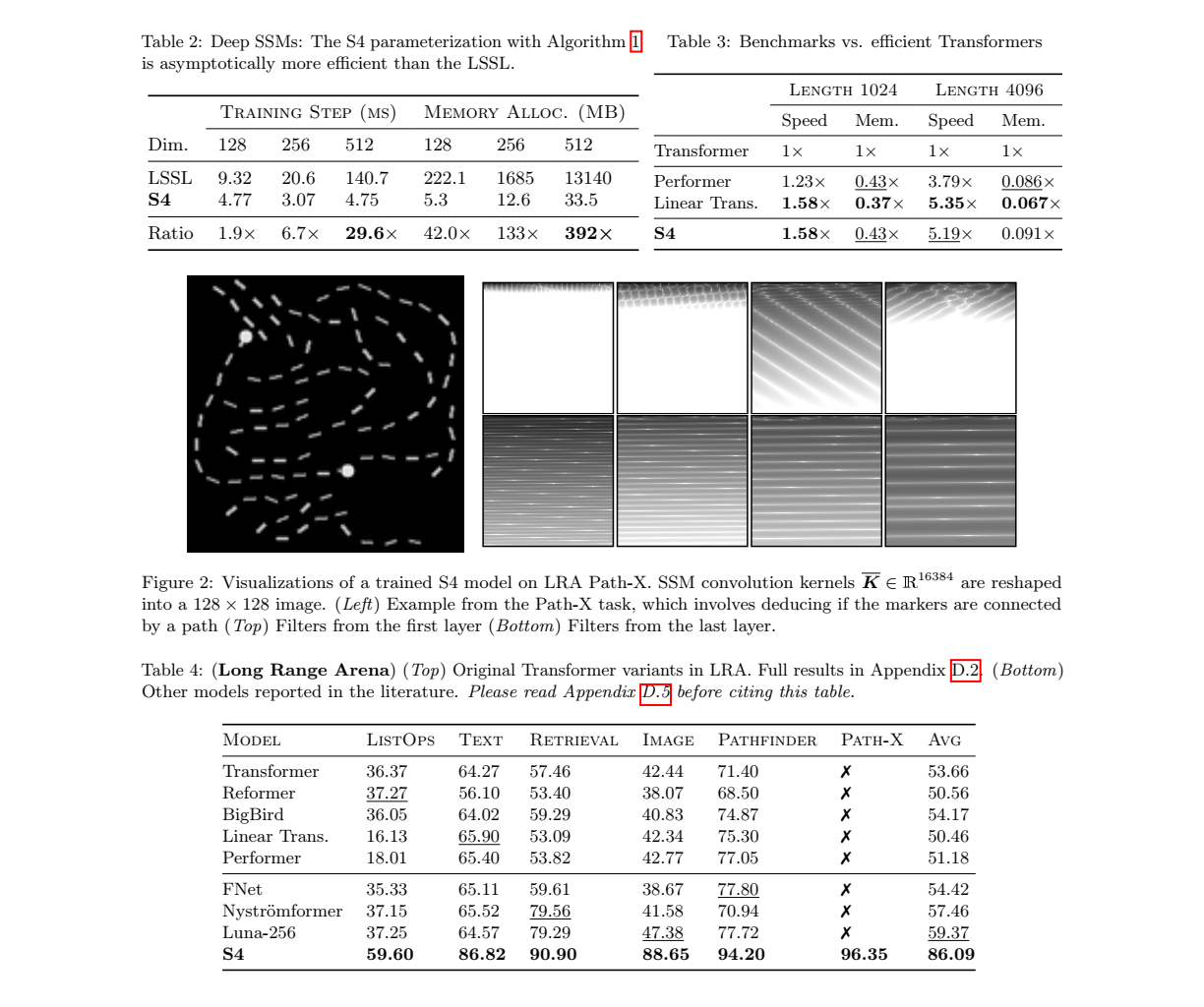
• 4.1 S4 Efficiency Benchmarks : S4는 기존의 상태 공간 모델 및 Transformer 모델에 비해 매우 빠른 학습 속도와 적은 메모리 사용량을 자랑합니다. 실험 결과, S4는 속도와 메모리 효율성 모두에서 우수한 성능을 보였습니다.

• 4.2 Learning Long Range Dependencies : Long Range Arena (LRA)** 벤치마크에서 S4는 장기 종속성을 처리하는 데 있어 탁월한 성능을 보여줍니다. 특히, 기존 모델들이 해결하지 못한 어려운 문제를 해결하는 데 성공하였습니다.

• 4.3 S4 as a General Sequence Model : S4는 이미지, 텍스트, 오디오 등 다양한 데이터 유형에서 사용될 수 있는 일반적인 시퀀스 모델로 제안됩니다. 실험을 통해 S4가 다양한 데이터 유형에서 뛰어난 성능을 발휘한다는 것을 확인할 수 있습니다.

• 4.4 SSM Ablations: the Importance of HiPPO : HiPPO 초기화를 사용한 상태 공간 모델이 성능 향상에 매우 중요하다는 것을 실험적으로 확인하였습니다.

---

Reference

Lectures

• Efficiently Modeling Long Sequences with Structured State Spaces (링크)

• Structured State Space Models for Deep Sequence Modeling (링크)

Blogs

• github.com/dhkim0225/1day_1paper
  • HiPPO, https://github.com/dhkim0225/1day_1paper/issues/54
  • LSSL, https://github.com/dhkim0225/1day_1paper/issues/51
  • S4, https://github.com/dhkim0225/1day_1paper/issues/52

• A Visual Guide to Mamba and State Space Models (링크)

Books

• Dive into Deep Learning (링크)

Papers

• HiPPO: Recurrent Memory with Optimal Polynomial Projections (2020)

  • 논문 링크: https://arxiv.org/pdf/2008.07669

• LSSL: Combining Recurrent, Convolutional, and Continuous-time Models with Linear State-Space Layers (2021)

  • 논문 링크: https://arxiv.org/pdf/2110.13985

• S4: Efficiently Modeling Long Sequences with Structured State Spaces (2022)

  • 논문 링크: https://arxiv.org/pdf/2111.00396