■ Adversarial serach problems
-이기는 게 우선순위(중요)가 아니라 내 순서가 왔을 때 현재 어디에 두는 것이 최선인지를 찾는 과정
-
Single-Agent Search Problems
-vacuum cleaner, 8-puzzle, path-finding, n-Queens,...
-이전까지 다뤘던 내용들은 single agent였음(나의 행동만 고려)
-모든 것이 나 혼자만 열심히 하면 되는 문제 -
Adversarial Search Problems(적대적 탐색 문제)
-Multi-agent Game problems
-ex)tic-tac-toe, go, chess, robot soccer, video shooting game
-상대와는 Competitive, 팀원간에는 Cooperative
-탐색의 결과물(목적)이 현재 상태에서 어디에 둘 것인가 - single action임
-내 행동을 결정할 때마다 search가 진행됨
■ 2-player game search tree
- MAX(X): 나(내 순서 레벨)
-둘 수 있는 곳이 9곳 존재(내가 먼저 시작), 어디를 결정 -> 탐색의 solution
-game search tree는 반드시 제일 위에 노드가 MAX임 - MIN(O): 상대(상대 순서 레벨)
-상대 순서일 때는 나는 탐색x, 내 순서일 때만 탐색이 진행됨
-내가 지면 -(음수), 비기면 0, 이기면 +(양수), 지고 이기고의 절대값은 동일(말단 상태의 평가)
-미래로부터 결론을 내서 거꾸로 거슬러 올라옴
■ Minimax Search(min(상대),max(나))
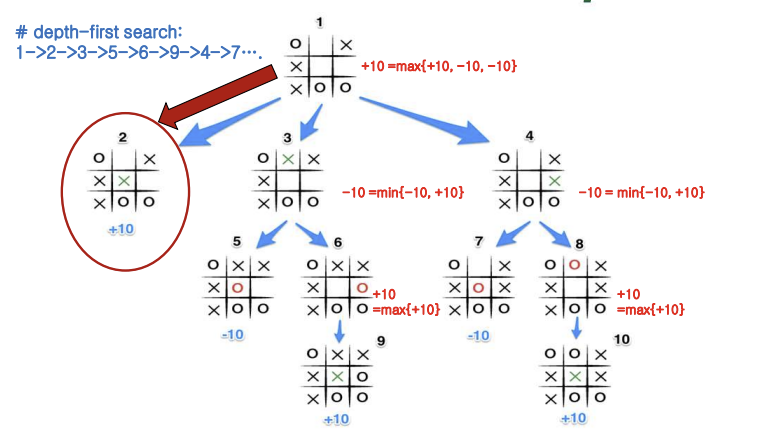
-depth-first search: 깊이 우선 탐색을 진행
-승부가 결정되는 말단 노드에 평가치(utility)가 존재
-비단말노드: 승부가 결정이 안된 노드(비단말노드도 평가치 계산 가능)
-비단말노드는 자식 노드의 평가치들 중에서 가장 높거나 낮은 값으로 결정, 만약 비단말노드가 max level이면 자식들의 평가치 중에서 가장 높은 값을 평가치로 사용, 만약 min level이면 자식들의 평가치 중에서 가장 낮은 값을 평가치로 사용
-루트노드가 평가치를 갖는 순간 탐색은 종료됨
-solution: 부모가 가지는 평가치에 해당하는 자식 노드를 선택하는 경로를 계속 진행
-깊이 우선 탐색을 진행하는데 말단노드가 생기는 경우가 이기거나 지는 상황이 됨
-상대방의 최선을 예측하지 않으면 내 최선의 선택도 결정하지 못함
-결론: 가상에서 나 뿐만 아니라 상대의 행동까지 결정해보면서 결과상태가 나한테 얼마나 유리한지 평가의 결과를 추려서 루트노드의 상태에서 어디로 간다라고 하는 매번 내 순서에서 행동 한 개를 결정하는 탐색이다.(여러 번 하게 됨)
→minimax search algorithm
-Perfect play for deterministic games
-깊이 우선 탐색
-Assumptions(가정들):상대도 나와 동일한 상태 평가 함수를 가지고 있다, 상대도 나처럼 최선의 선택을 할 것이다
-idea: choose move to position with highest minimax value = best achievable payoff against best play
-
Properties of minimax algorithms
-완전성: Yes, 트리가 유한 개일 때 무조건 말단노드까지 가게 됨 즉, 무한루프에 빠질 일이 없음, 항상 결정을 할 수 있음
-최적성: Yes, 나한테 최악의 수는 상대방에게 최선의 수임 즉, 나는 항상 최선의 수를 선택해서 말단노드까지 이동 후 탐색이 종료되기 때문에 나는 항상 최선의 수를 선택
-time: O(b^m)/ b(branching factor): 루트에서부터 평균적으로 자식이 몇 개씩 생기는지, m: 깊이, 얼마만큼 내려가는지
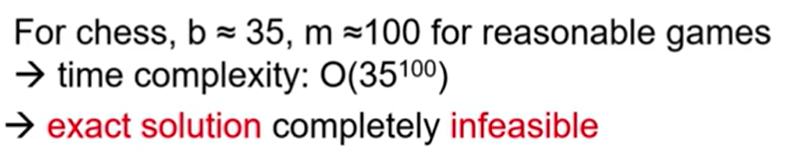
-space: O(bm) -
Time / Resource Limits(시간/계산자원 제한)
-해결책: depth limit(깊이 제한), cutoff(탐색 절단), evaluation function(상태 평가 함수)
■ minimax Cutoff Search
-이전의 minimax search의 말단노드 테스트와는 다르게 Cutoff-test가 수행됨, Utility가 Eval로 대체됨
-깊이 제한을 얼마나 줘야하는 지가 또 문제가 됨

- tic-tac-toe game
-the evaluation function, e(p)
-if p is a win for Max(내가 이기면), e(p) = 무한대 or +100
-if p is a win for Min(상대가 이기면), e(p) = 음의 무한대 or -100
→이긴 것도 아니고 진 것도 아닐 때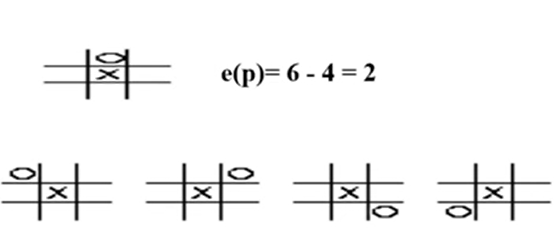
e(p) = 내가 이길 가능성이 있는 경우의 수 - 상대방이 이길 가능성이 있는 경우의 수
-위의 그림에서 내(x)가 가운데에 있고 상대가 바로 위에 두었을 경우 내가 이길 가능성이 있는 경우의 수는 6임
-반대로 상대의 위치에서 상대가 이길 수 있는 경우의 수는 4임
-즉, e(p) = 6 - 4 = 2 / 양수이면 내가 유리, 음수이면 상대가 유리
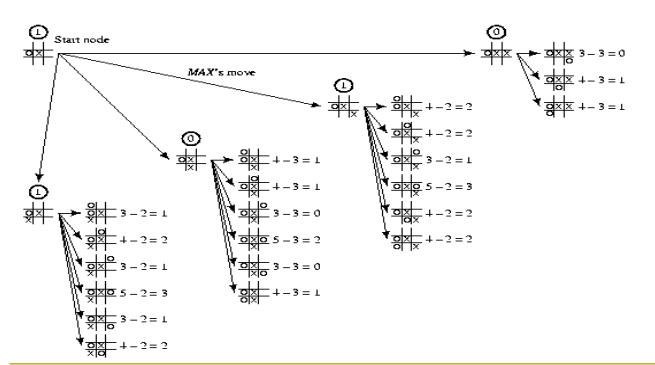
-위 그림에서 아래의 4가지 경우는 다 동일한 경우임The First Stage
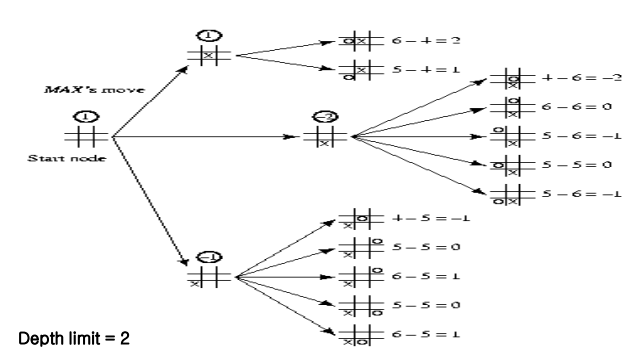
-위치 상 회전시켰을 때 동일한 경우들이 존재하기 때문에 대표하는 하나의 경우로 통합해서 나타냄
→그림 오류 발견
-마지막 min value가 -1인 경우의 자식들 중 세 번째의 경우에 상대방(min)의 수가 휴대폰 다이얼 위치 기준 3이 아닌 6에 있어야 함The Second Stage
-나는 항상 상대방이 최선의 수를 둘 것이라고 생각하고 계산했기 때문에 상대방이 어떻게 두든 나는 고민할 필요 없음 즉, 나는 항상 최선의 수를 둘 수 밖에 없는 것임The Last Stage
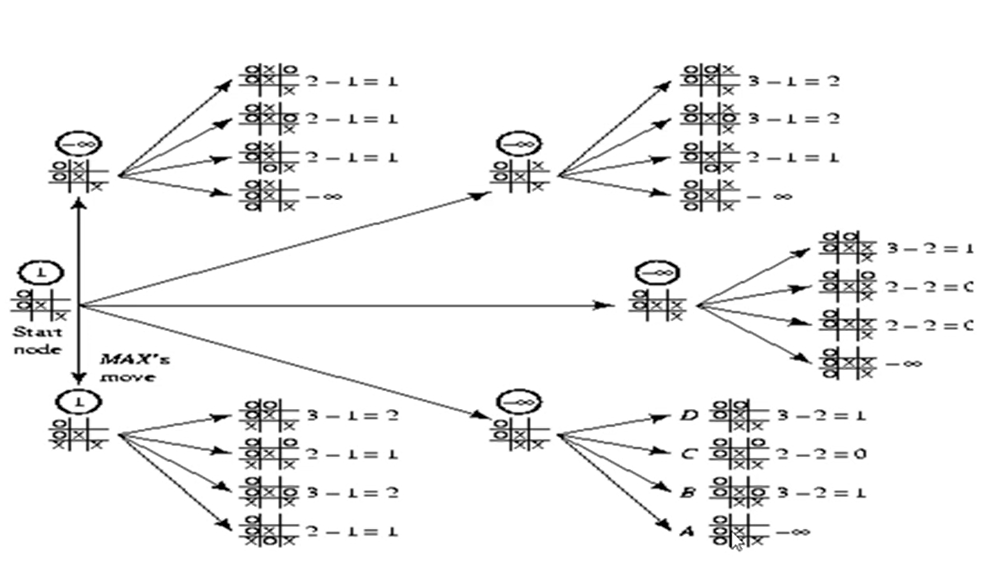
-자식 노드의 평가치가 1인 경우를 제외하고 나머지는 다 음의 무한대임 why? 내가 항상 최선의 수를 생각하듯이 상대도 최선의 수를 둔다고 가정하기 때문에 상대방이 7번자리에 수를 두면 항상 질 수 밖에 없다고 여기게 됨
■ 알파-베타 가지치기
-알파 value: max node의 하한선(이 값보다는 크거나 같을 거야라는 값, 탐색을 진행하면서 자식노드 중에서 평가치가 더 큰 값이 나오면 갱신되겠지)(자식 노드의 평가치가 공개된 게 아직 별로 없을 때
-베타 value: min node의 상한선(이 값보다는 작거나 같을 거야, 자식노드 중 평가치가 더 낮은 값이 나오면 갱신)
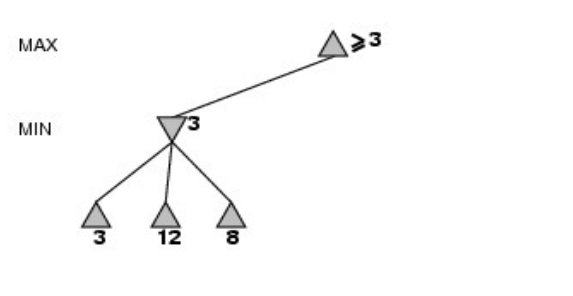
-MIN 자식들 중 가장 작은 값인 3으로 업데이트
-MAX value는 현재 자식노드가 하나 뿐이므로 그 값(3)보다 크거나 같아야 함
-새로운 자식 노드 등장
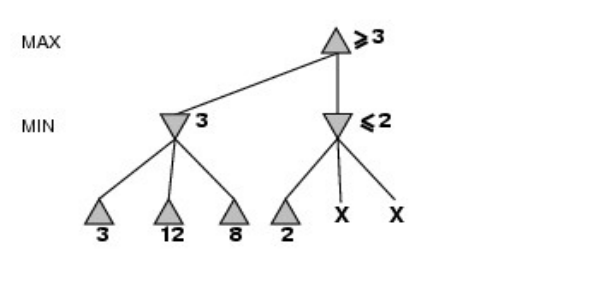
-MIN노드 탐색 중 첫 번째 자식노드 value가 2, MIN value는 2보다 작거나 같게 됨
-MAX value가 현재 3보다 크거나 같아야 하는데 두 번째 자식노드의 value가 2보나 작거나 같음 -> 더 이상 그 자식노드는 탐색을 진행할 필요가 없음 즉, 알파 가지치기 수행
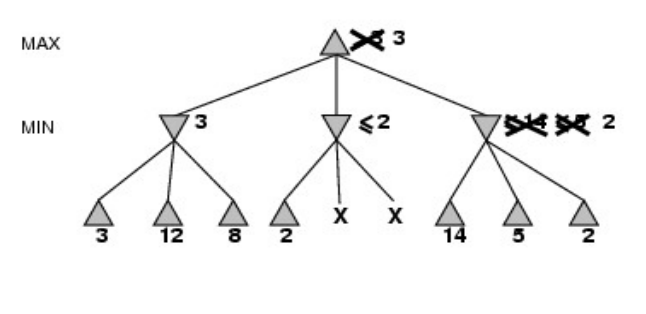
-세 번째 자식 노드의 자식들이 각각 14, 5, 2의 value를 가지고 있었기 때문에 MIN value도 탐색이 진행될 때 마다 갱신되다가 MIN의 자식노드 탐색이 종료되어 노드들이 확정된 순간 가장 작은 값으로 업데이트
-마찬가지고 MAX 노드에 대해서도 자식노드들의 value들이 확정되었기 때문에 3보다 크거나 같다가 아니라 3으로 확정하며 업데이트
- Rules for 알파-베타 Pruning(가지치기)
→ alpha Cutoff rule
-현재 MIN 노드이고 부모노드가 MAX일 때 MIN 노드 즉, beta 노드의 벨류값이 MAX 즉, alpha노드(부모)의 벨류값보다 작거나 같으면 탐색 종료(가지치기)
-MIN 노드 밑의 가지를 자르는 것
→ beta Cutoff rule
-현재 MAX 노드이고 부모노드가 MIN일 때 MAX 노드 즉, alpha 노드의 벨류값이 MIN 즉, beta노드(부모)의 벨류값보다 크거나 같으면 탐색 종료(가지치기)
-MAX 노드 밑의 가지를 자르는 것
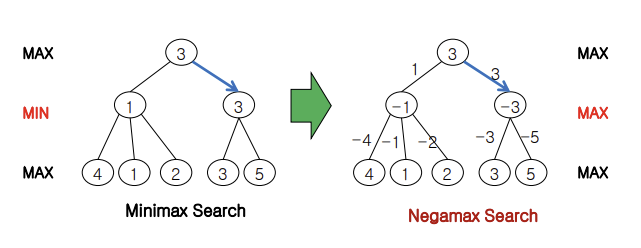
- Negamax Algorithm
-minimax search algorithm을 간략화한 변형
-MAX value 노드들의 value를 통해 MIN value 값을 구할 때 MAX 노드들의 value 값들의 부호를 뒤집어서 MIN value를 구하고 이렇게 구한 MIN value의 노드들을 비교해서 MAX value를 구할 때에도 부호를 바꾼 후 비교해서 MAX value 작성