■ Local Search Algorithms(지역 탐색 알고리즘들)
ex) n-queens

→특징: 초기 상태가 임의로 설정됨, 이후 계속 고쳐가면서 목표상태에 도달
→이때 f()는 평가 함수(평가치)를 뜻함
→기존 알고리즘들은 초기상태와 목표상태를 알고 과정을 알기 위함임 / 또한 선택할 수 있는 갈림길은 만나면 깊이가 깊은 것부터 먼저 가되 나머지는 다 저장소에 저장되어 있기때문에 완전한 알고리즘을 추구
→local search는 기존 알고리즘들과 다르게 하나(도메인)를 선택해서 옮겨보면서 평가치가 좋은 것을 선택, 선택할 수 있는 갈림길을 만나면 평가치가 좋은 것을 선택하고 백트래킹 하지 않음 즉, 선택되지 않은 도메인들은 신경쓰지 않음
→최적화 문제들에 대부분 쓰일 수 있음
→이는 상태 공간 탐색이므로 상태를 결정하는 변수들이 결정되어야 함( ex) v1, v2, v3, v4
→변수에다가 값을 줄 때마다 상태가 바뀌는데 그 상태가 얼마나 좋은지 안 좋은지를 결정하는 평가함수가 필요함
→평가 함수가 좋아지는 쪽으로 즉, 최대가 될 때까지 지속해야함 / 만약 평가 함수가 더 좋아지지 않으면 그게 답이되고 stop 상태가 됨
→목표 상태 자체가 답이기 때문에 경로찾기와는 무관함
■ Hill-Climbing Search(언덕 오르기 탐색)
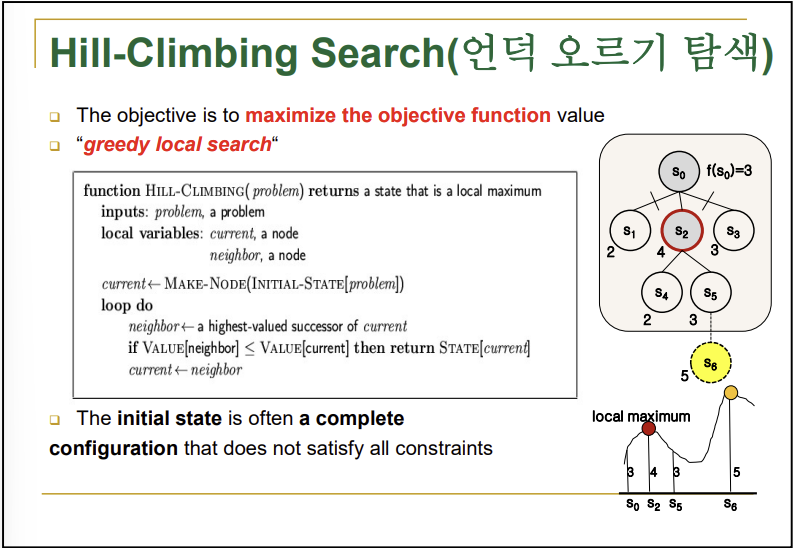
→순수 local search를 의미, 역시 똑같이 초기 상태 랜덤
→만들어진 자식들 중에서 평가치가 제일 높은 것을 고르고 부모와 비교, 이후 자식이 부모보다 평가치가 더 높으면 current를 이동, 다른 동일 레벨 자식들과 부모는 잘라버리고 이 과정을 반복
→만약 자식과 부모의 평가치를 비교했을 때 부모의 평가치가 더 높으면 굳이 옮길 필요가 없음, 즉 부모인 본인이 그래프 상에 꼭대기에 있기 때문에 이를 goal로 하고 탈출 -> 언덕 오르기가 이를 뜻하는 것임
→근데 만약 자식 다음 자식 즉, 본인 이후 두 레벨 뒤에 있는 자식이 본인의 평가치보다 높을 때 local maximum(or local minimum) 문제가 발생 / 위 사진의 경우에 S2:4, S5:3, S6:5일 때 문제 발생
→이 경우에 local maximum 즉 지역 최대 평가치는 S2:4이고 global maximum은 S6:5임
→이 local maximum에서 global maximum을 찾기 위한 알고리즘들이 밑에 등장할 세 가지 알고리즘들임, 하지만 아직 이 문제를 완벽히 해결하기 위한 방법은 존재하지 않음
→그렇다고 해서 local search를 사용하지 않을 수는 없음
■ Simulated Annealing Search(모의 담금질 탐색)

→평가치가 제일 낮은 지점을 찾음(global minimam)
→bad moves 즉, 평가치가 낮아지더라도 허용함 단, 제약을 둠
→greedy, hill-climbing은 초반부터 끝까지 보수화 작업을 이어감, 하지만 bad moves를 열어놔야 global maximam을 찾아가는 즉, 그래프를 넘어설 수 있음
- pseudo code
→ t: time
→ T: temperature(온도), T가 낮아지면 행위 종료
→ T <- schedule[t]: 시간이 지남에 따라 T가 감소
→ current(부모)가 자식을 랜덤으로 하나만 만들어서 선택: next(자식)
→ Value: 평가치
→ △E <- Value[next] - Value[current]
→ if △E > 0 then current <- next: 자식이 부모보다 평가치가 높으면 바꿈 => good move
→ else current <- next only with probability e^△E/T: 자식이 부모보다 평가치가 낮음 => bad move 이때 시간 t가 증가함에 따라 bad move의 확률을 점차 낮춤
■ Local Beam Search(지역 다발 탐색)

→이전까지의 탐색은 single state 탐색
→이건 다수 즉, 동시에 여러 개를 탐색함
→시작 state를 여러 개 즉, 초기상태를 여러 개를 만듦(k개)
→k개의 각각마다 자식을 생성하고 이를 평가해서 다시 k개만 남겨놓음, 이를 반복해서 평가치가 좋은 k개를 계속 유지해서 goal에 도달하는 방법
→별로 기대를 채우지 못함
→랜덤으로 다르게 출발했는데 그 하나하나가 만든 자식들을 평가할 때 동일한 기준으로 평가하게됨 -> 결과적으로 남아있는 것들이 다 비슷해짐
→결국 조기에 다양성을 잃어버리고 거의 수렴하게 됨(원치 않은 조기 수렴) == 평가 기준에 따라 한 쪽으로 몰리게 됨
→결국 다수의 경우에 local minimum에 빠지게 됨
→샘플링이 매우 중요하게 됨(샘플 숫자보다 샘플 자체가 얼마나 많은 것들을 대변할 수 있는지가 중요)
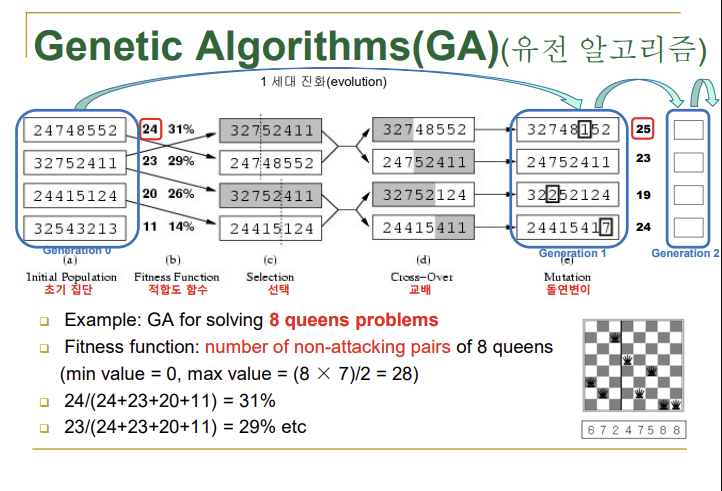
■ Genetic Algorithms(GA)(유전 알고리즘)

→k개의 랜덤하게 만든 상태에서 시작
→string 형태로 상태가 표현되어야 함
→crossover(교배): 부모의 교배(crossover)를 통해서 자식을 생성 => 위 사진의 화살표를 기준으로 뒷 부분의 string을 서로 교환
→mutation(돌연변이): 이때 자식이 임의의 비트를 골라 다른 값(난수로)으로 바꾸어버리기도 하는데 이를 돌연변이(mutation)라고 함
→selection(선택): 기존에 있던 k개의 상태 중에서 평가를 해서 평가치가 비교적 높은 것들을 교배시켜서 돌연변이를 발생시키며 자식을 생성
→위 세 가지가 유전 알고리즘의 강점이라고 할 수 있음
→적합도 함수(fitness function)를 평가함수라고 생각해도 됨
- n - queens
→8C2 = 28, 28에서 attacking(충돌)수를 뺀게 적합도 함수
→위 사진의 초기 집단에서 마지막 string처럼 적합도 함수치가 너무 낮으면 도태시켜버림(교배에 포함시키지 않음)
→위 사진의 selection에서 점선이 유전정보에서 교환할 양을 의미
→점선을 결정하는 과정도 랜덤인 난수로 결정
→교배 후 바로 자식으로 결정하는 게 아니라 돌연변이 과정을 거쳐서 생성(실상 돌연변이는 1%미만으로 발생시킴)
→진화 과정에서 다 좋아지는 걸 바라는게 아니라 현재 세대에서 가장 좋은 값이 과거 세대보다 좋아지길 바라는 것
→다 좋아질 필요가 없는 이유는 답은 결국 하나이기 때문임- GA for Maze Solving
→red dot: 목표(도달점)
→pink: 폭탄
→gray: 장애물
→Gene Size: 각 이동 계획의 길이, 최소 거리(minimam) * 2 / 최소 거리는 현재 상태에서 목표상태까지 폭탄, 장애물을 무시하고 갈 수 있는 최단 거리를 말함(가로+세로)
→Population Size: 이동 계획의 수(경로를 찾을 때 개수를 최대 몇 개를 유지해라), 최종적으로 출발지부터 목적지까지 갈 수 있는 경로가 나오게 됨
→the fitness: 최대 도달 지점과 목표가 얼마나 근접했는지, 즉 거리가 0이 될 때까지 진행함- GA의 특성
→상태를 스트링으로 인코딩
→local beam처럼 여러 개의 상태들을 동시에 탐색(병렬 탐색)
→탐색에 적합도 함수를 이용
→확률적인 상태 전이, 난수로 결정
- 마무리
→목표상태 자체가 답, 과정은 필요 없음
→어떤 과정을 거치던지 가장 좋게 평가되는 것을 찾음(최적화 문제를 풀기위한 방법)
→문제가 다르기 때문에 적용할 탐색 알고리즘이 다름→임의로 설정된 변수 값의 초기상태에서 변수를 조금씩 바꾸며 현재 상태보다 더 평가치가 좋은게 나오면 옮겨감, 더 이상 더 좋은 평가치가 없으면 거기서 멈추고 그 상태가 답이됨(Hill-Climbing)
→이때 hill-climbing은 local maximam 문제가 존재하기 때문에 평가치가 나빠도 건너가게 하는 방법인 Simulated Annealing(모의 담금질)
→그렇지만 그것보다 차라리 여러 개를 만들어서 돌리면 그 중 하나는 global maximam까지 갈 수 있지 않을까?(병렬 탐색) Local Beam(지역 다발)
→하지만 이것도 다양성을 쉽게 잃어버리니까 GA(유전)