지금까지 공부했던 내용들을 정리한 문서입니다. 참고 서적을 정리한 내용도 있지만 제가 알고 있는 지식을 기반으로 정리한 내용도 있기 때문에 틀린 부분이 있을 수 있습니다. 혹시 발견하신다면 피드백 부탁드립니다 😁

또한 이 문서는 군집화와 군집화 알고리즘의 개념적인 부분을 다룹니다. 좀 더 심화된 이론이 필요하신 분은 다른 글을 참고해 주세요 😋

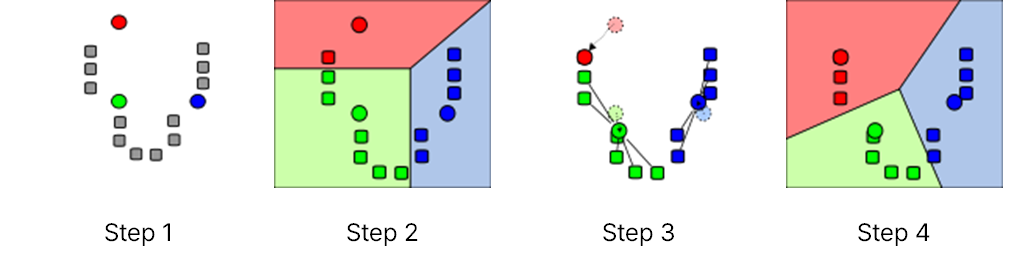
군집화(clustering)란, 데이터의 특성을 분석하여 유사한 속성을 갖는 데이터끼리 하나의 군집(cluster)으로 묶는 작업을 의미한다. 여기서 유사한 속성을 갖는 데이터란 특정 데이터 공간에서 비슷한 구역에 위치한 데이터 점들을 말한다. 기계학습 알고리즘 중 비지도 학습에 속하는 방법이며, 데이터 분석에서 군집화 기법을 이용하면 데이터가 굉장히 많아도 데이터의 특성을 파악하기 비교적 쉬워진다. 군집화 기법은 소프트 클러스터링과 하드 클러스터링으로 세분화될 수 있다.

군집화 예시

💡 소프트 클러스터링과 하드 클러스터링

• 소프트 클러스터링(soft clustering): 각 데이터가 여러 개의 군집에 속할 수 있는 방법
• 하드 클러스터링(hard clustering): 각 데이터가 오직 한 개의 군집에만 속할 수 있는 방법

✅ 거리 함수(Distance Function)

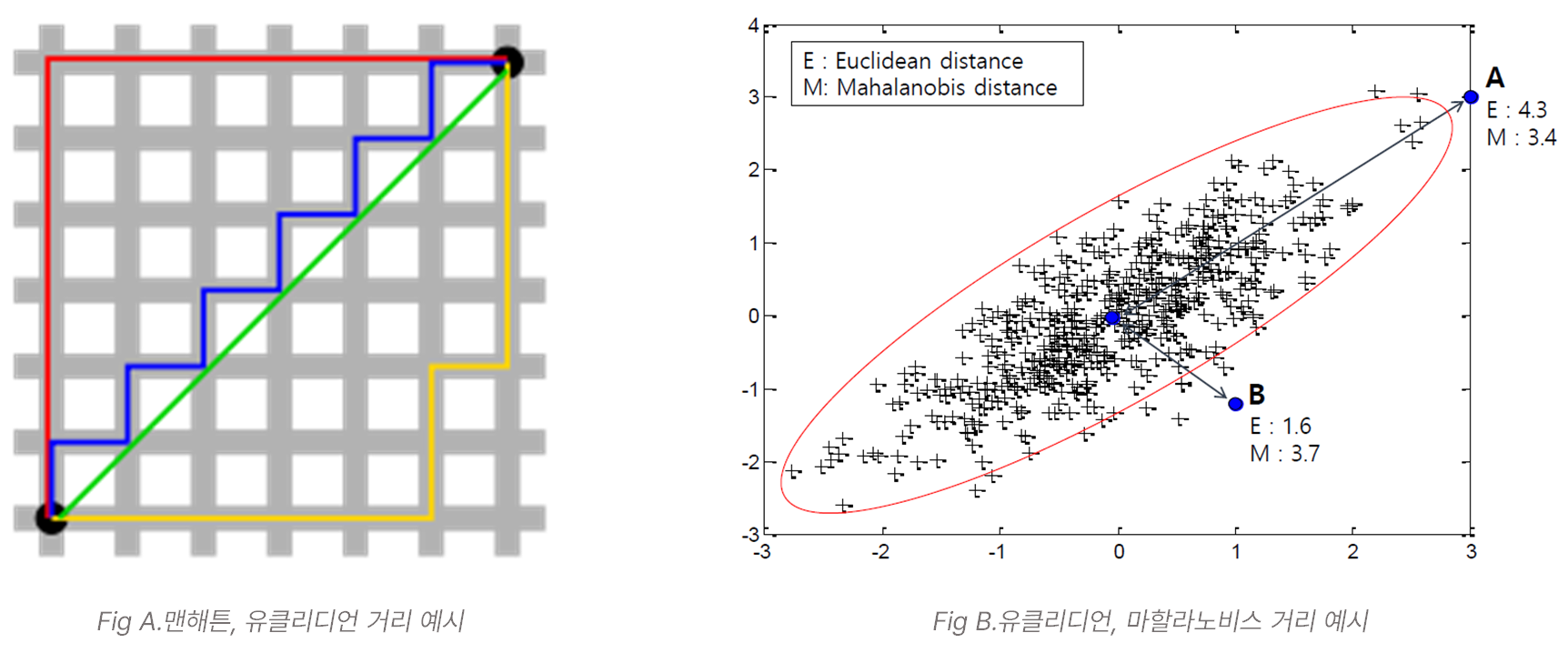
데이터 점들을 특징짓기 위해 군집화에서는 기본적으로 거리 함수(distance function)를 사용한다. 거리 함수는 말 그대로 두 원소 쌍(여기서는 데이터 샘플 간) 사이의 거리를 계산하는 함수로써, 군집화에서는 보통 그 값이 작으면 비슷한 속성(혹은 비슷한 공간에 위치)을 가지고 있다고 판단한다. 대표적인 거리 함수는 다음과 같으며, 일반적으로 유클리디언 거리가 많이 사용된다.

거리 함수 종류	설명
맨하탄 거리 (Manhattan Distance, L1 Norm)	두 점이 존재하는 좌표에서 각 차원 별 거리의 합 (Fig A 빨간선, 파란선, 노란선)
유클리디언 거리 (Euclidean Distance, L2 Norm)	두 점의 최단 거리 (Fig A 초록선)
마할라노비스 거리 (Mahalanobis Distance)	표본 점과 분포 사이의 거리, 표준 편차 개수를 기준으로 y가 평균에서 얼마나 떨어져 있는지를 나타냄 (Fig B 참고)
상관계수 거리 (Correlation Distance)	데이터 간의 피어슨 상관계수 값, 데이터 전체의 경향성을 비교하기 위한 척도

Fig A 출처, Fig B 출처

✅ 군집화 결과 평가 하기

군집화 알고리즘을 통해 만들어진 군집이 잘 만들어졌는지 평가하기 위한 척도가 존재한다. 여러 지표가 존재하지만 유명한 지표들은 다음과 같다.

군집화 평가 지표	설명
Dunn Index	군집 내(Intra Cluster) 요소간 최대 거리에 대한 군집 간(Inter Cluster) 거리의 최소 거리의 비를 계산한 지표, 값이 작을수록 군집화 결과가 좋음을 의미
Silhouette 계수	각 데이터의 그 데이터가 속한 군집 내(Intra Cluster) 요소들과의 유사도와 인접한 군집과의 유사도를 비교하는 지표, 값이 클수록 군집화 결과가 좋음을 의미

💡 (참고) 군집화 평가 지표 수식

1. Dunn Index

• $\delta(C_i, Cj)$: 군집 $i$와 $j$ 간의 거리
• $\triangle_k$: $k$번째 군집 내 거리

2. Silhouette 계수

• 자세한 계산 방법은 링크 참고
  $SC = \underset{\kappa}{\max}\ \tilde{s}(\kappa)$

군집화 알고리즘

---

1️⃣ K-평균 군집화 (K-means Clustering)

K-평균 군집화는 대표적인 군집화 알고리즘으로, 주어진 데이터 셋을 K개의 군집으로 나누는 작업을 수행한다. K-평균 군집화를 수행하기 위해서는 K값을 사람이 직접 설정해 주어야 한다. K-평균 군집화가 수행되는 과정은 다음과 같다.

💡 K-평균 군집화 프로세스

1. k개의 데이터 표본을 선택하여 군집 중심점(centroid)으로 정한다. (초기값 설정 과정)
2. 군집 중심점으로 선택된 데이터 표본을 제외한 다른 데이터들은, 군집 중심점과의 거리(distance)를 계산하여 가장 가까운 군집에 할당한다.
3. 모든 데이터의 군집이 결정되었다면, 할당된 데이터들을 기준으로 군집의 중심점을 다시 계산한다. (군집 중심은 클러스터 내 데이터들의 평균값으로 계산된다.)
4. 최적의 군집이 만들어질 때까지 2번과 3번이 반복적으로 수행된다. (군집 중심 변동이 거의 없을 때까지 수행)

그림출처

scikit-learn 라이브러리를 사용하여 Python3으로 구현하면 다음과 같다.

K-평균 군집화를 수행하기 전 초기 군집 중심점을 정할 때 사용하는 방법들이 존재한다. 여러 방법이 있지만 아래 예제에서는 k-means++ 방법을 사용하니 참고하자.

• k-means++: 초기에 무작위로 선택된 중심점을 기준으로 각 데이터 간의 거리를 계산하여 거리 비례 확률에 따라 다음 중심점을 정하는 방법, 처음에 선택된 중심점으로부터 최대한 먼 곳에 위치한 점을 선택하여 군집을 잘 나눌 수 있도록 함, k개가 될 때까지 반복

from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
from pandas import DataFrame
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt

# Generate data samples
np.random.seed(1)
data, _ = make_blobs(n_samples=1000, centers=5, cluster_std=0.8)

# Fit kmeans model
KMeans = KMeans(n_clusters=5, init="k-means++")
KMeans.fit(data)

# Label of each point
labels = KMeans.labels_ 
print('labels: ', labels) 

# Coordinates of cluster centers
centroids = KMeans.cluster_centers_ 
print('centroids: ', centroids)

# Make dataframe
df = DataFrame({'X':data[:,0], 'Y': data[:,1]})

# Visualize clustering result
plt.figure(figsize=(15, 10))
sns.scatterplot(x="X", y="Y", data=df, hue=labels, palette='coolwarm')
plt.scatter(centroids[:, 0], centroids[:, 1], c='red', alpha=0.5, s=150)

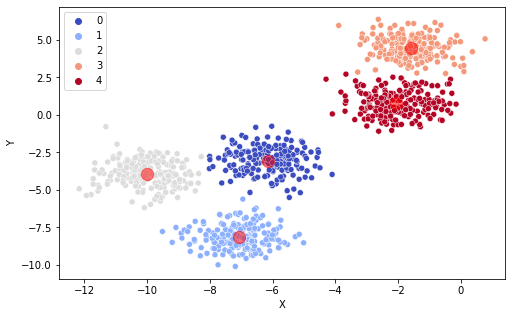K-평균 군집화 결과

2️⃣ 계층적 군집화 (Hierarchical Clustering)

계층적 군집화란 트리 모형을 이용해 개별 개체들을 순차적, 계층적으로 유사한 개체 내지 그룹과 통합하여 군집화를 수행하는 알고리즘이다. K-평균 군집화(K-means Clustering)와 다르게 사전에 군집 수를 정해주지 않아도 학습이 가능하다. 계층적 군집화는 보통 덴드로그램(dendrogram)이라고 하는 그래프를 이용해 시각화 할 수 있으며, 일정 높이에서 덴드로그램을 자르는 방식으로 군집의 개수를 정한다. 계층적 군집화는 합병에 의한 방법(agglomerative)과 분할에 의한 방법(divise)으로 나눌 수 있다.

그림참고

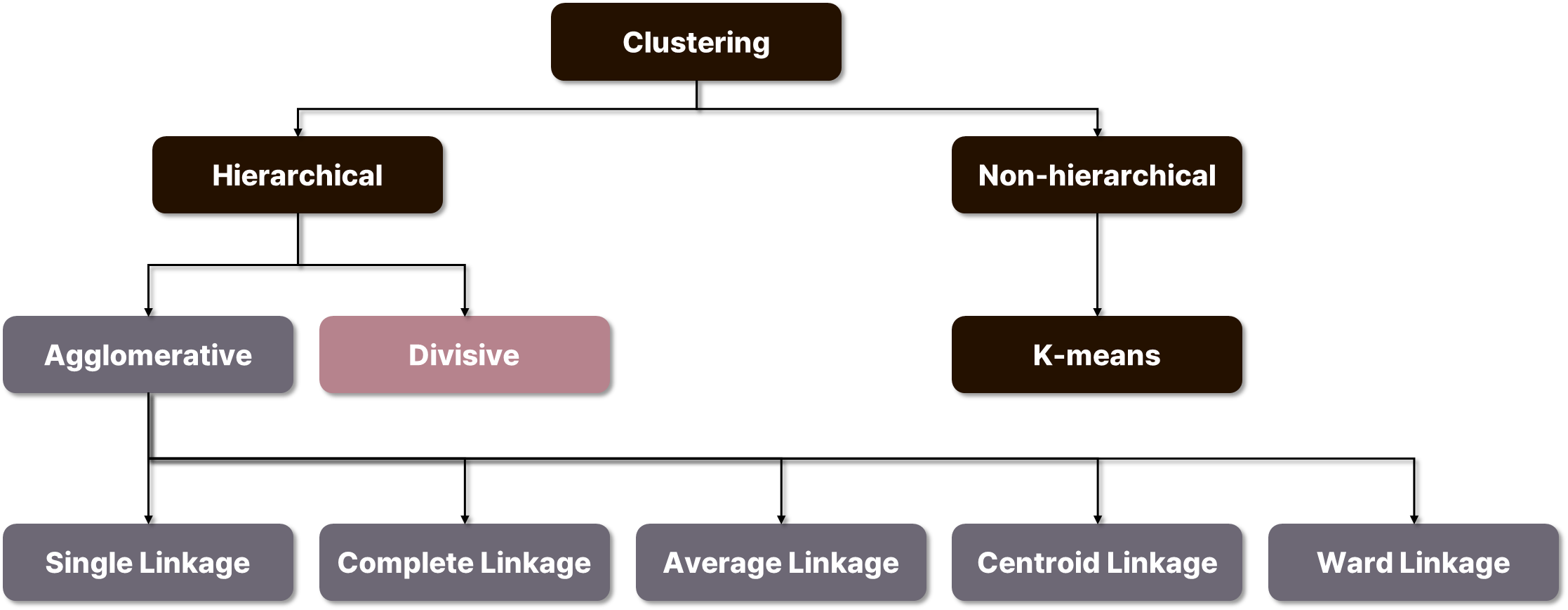
✅ 합병에 의한 방법(Agglomerative methods)

💡 계층적 군집화 프로세스 - 합병

1. 1개의 개체를 가지는 n개의 군집을 생성한다.
2. 군집 간의 거리를 계산하여 가장 유사한 군집 쌍을 찾아 하나의 군집으로 묶는다.
3. 2를 반복하여 모든 데이터가 하나의 군집이 될 때까지 군집 합병을 수행한다.

합병에 의한 계층적 군집화 방법에서, 군집 간 거리를 계산하기 위해 사용되는 여러 가지 방법이 존재하며, 데이터에 따라 군집화가 잘 되는 방법을 선택하면 된다. 종류는 다음과 같다.

이름	설명
최단 연결법 (Single Linkage method)	군집 내의 데이터 간 거리 중 가장 작은 값을 군집 간 거리로 설정하는 방법
최장 연결법 (Complete Linkage method)	군집 내의 데이터 간 거리 중 가장 큰 값을 군집 간 거리로 설정하는 방법
평균 연결법 (Average Linkage method)	군집 내의 데이터 간 거리에서 평균한 값을 군집 간 거리로 설정하는 방법
중심 연결법 (Centroid Linkage method)	군집의 중심(centroid) 간의 거리를 군집 간 거리로 설정하는 방법
Ward 연결법 (Ward Linkage method)	ward: (두 군집 간 제곱합 - (군집 내 제곱합의 합))를 군집 간 거리로 설정하는 방법

Scipy 라이브러리를 사용하여 Python3으로 구현하면 다음과 같다.

아래 예제는 Wholesale customers data 데이터를 사용하여 구현한 예제이므로, 사전에 다운로드가 필요합니다.

from scipy.cluster.hierarchy import linkage, dendrogram
from sklearn.preprocessing import normalize
import matplotlib.pyplot as plt
import pandas as pd

# dataset URL
# https://archive.ics.uci.edu/ml/machine-learning-databases/00292/Wholesale%20customers%20data.csv
data = pd.read_csv('Wholesale customers data.csv')

data_scaled = normalize(data)
data_scaled = pd.DataFrame(data_scaled, columns=data.columns)

linkage_list = ['single', 'complete', 'average', 'centroid', 'ward']

fig, axes = plt.subplots(nrows=3, ncols=2, figsize=(15, 10))
for i in range(len(linkage_list)):
    hierarchical = linkage(data_scaled, method=linkage_list[i])
    dn = dendrogram(hierarchical , ax=axes[i%3][i%2])
    axes[i%3][i%2].title.set_text(linkage_list[i])

plt.tight_layout()
plt.show()

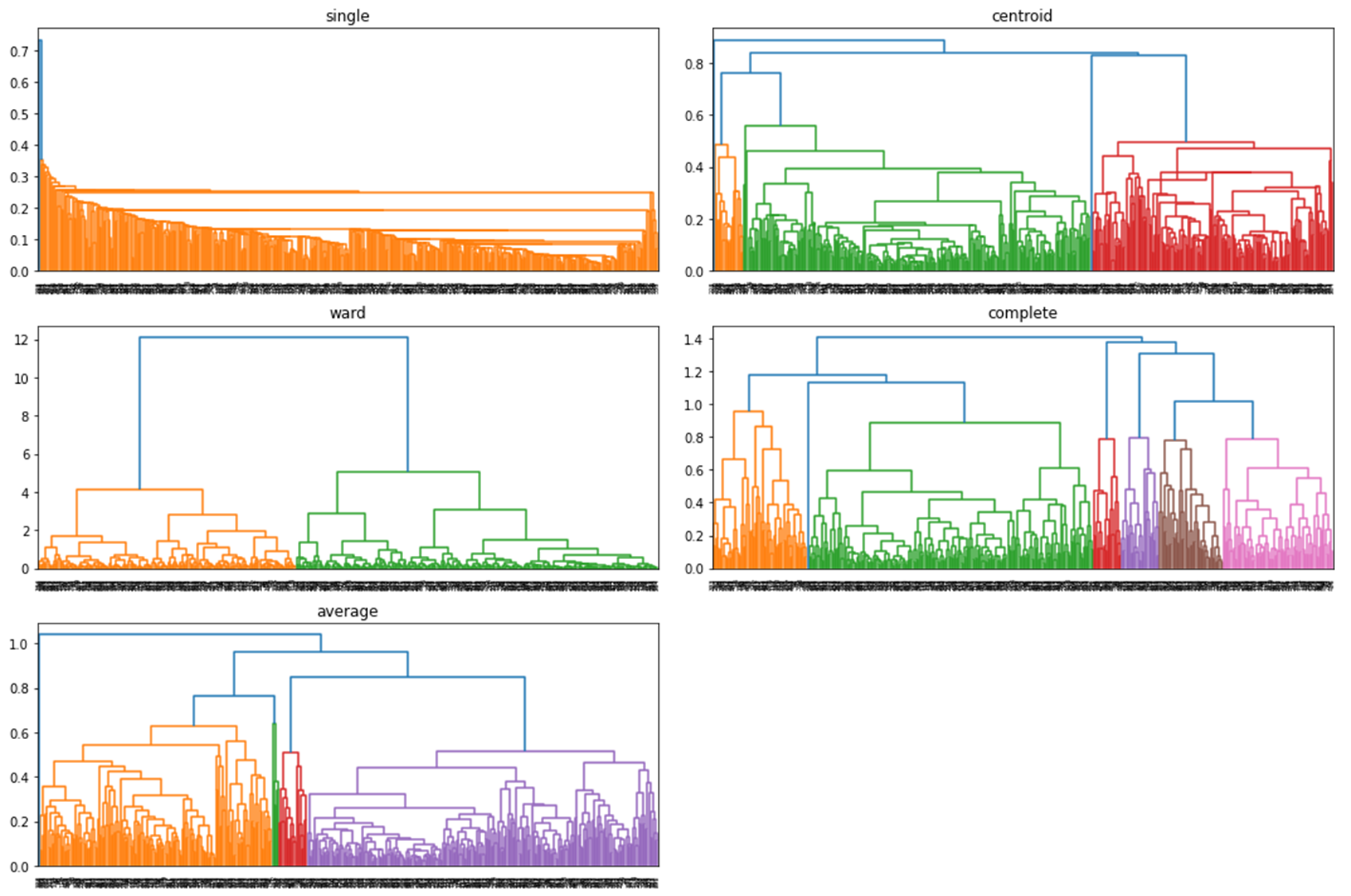합병에 의한 계층적 군집화 결과, 군집 거리 계산 방법 별 덴드로그램

✅ 분할에 의한 방법(Divisive methods)

합병에 의한 계층적 군집화 방법과는 반대로 하나의 군집에서 시작하며, 1개의 개체가 하나의 군집이 되는 순간까지 군집을 분할해 나가는 방식으로 군집화를 수행하는 방법이다.

💡 계층적 군집화 프로세스 - 분할

1. 모든 데이터가 속해 있는 하나의 군집에서 시작한다.
2. 군집을 가장 유사하지 않은 두 개의 군집으로 나눈다.
3. 2를 반복하여 각 데이터가 하나의 군집이 될 때까지 군집 분할을 수행한다.

(코드 구현 예정)

3️⃣ 밀도 기반 군집화 (DBSCAN)

밀도 기반 군집화(Density-based spatial clustering of application with noise)는 주어진 데이터의 밀도를 기반으로 군집화를 수행하는 알고리즘으로, 데이터 점 간 거리를 이용하여 클러스터링 하는 K-평균 군집화, 계층적 군집화와는 다르게, 데이터가 모여있는, 즉 밀도가 높은 부분을 찾아 군집화하는 방법이다.

밀도 기반 군집화의 과정에 앞서 학습 과정 이해를 위해 필요한 기본 하이퍼 파라미터와 주요 개념을 소개한다.

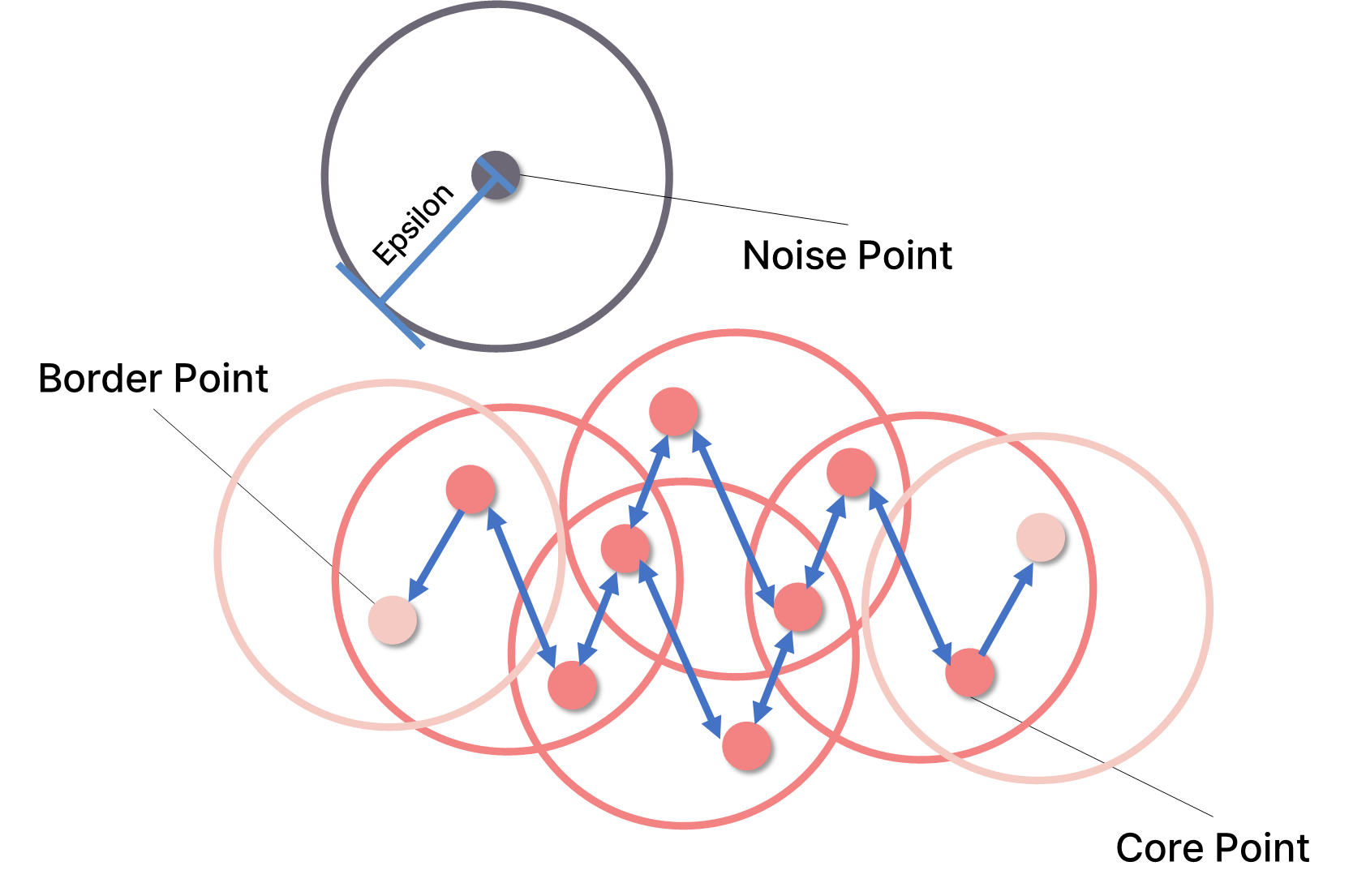
✅ 밀도 기반 군집화(DBSCAN) 기본 하이퍼 파라미터

이름	설명
엡실론 (epsilon)	어떤 한 점으로 부터의 거리
점 최소 개수 (min_samples)	어떤 점을 핵심 점(중심점)으로 간주하는 점들의 최소 개수

점 최소 개수(minpts)가 4개인 경우

✅ 밀도 기반 군집화(DBSCAN) 주요 개념

이름	설명
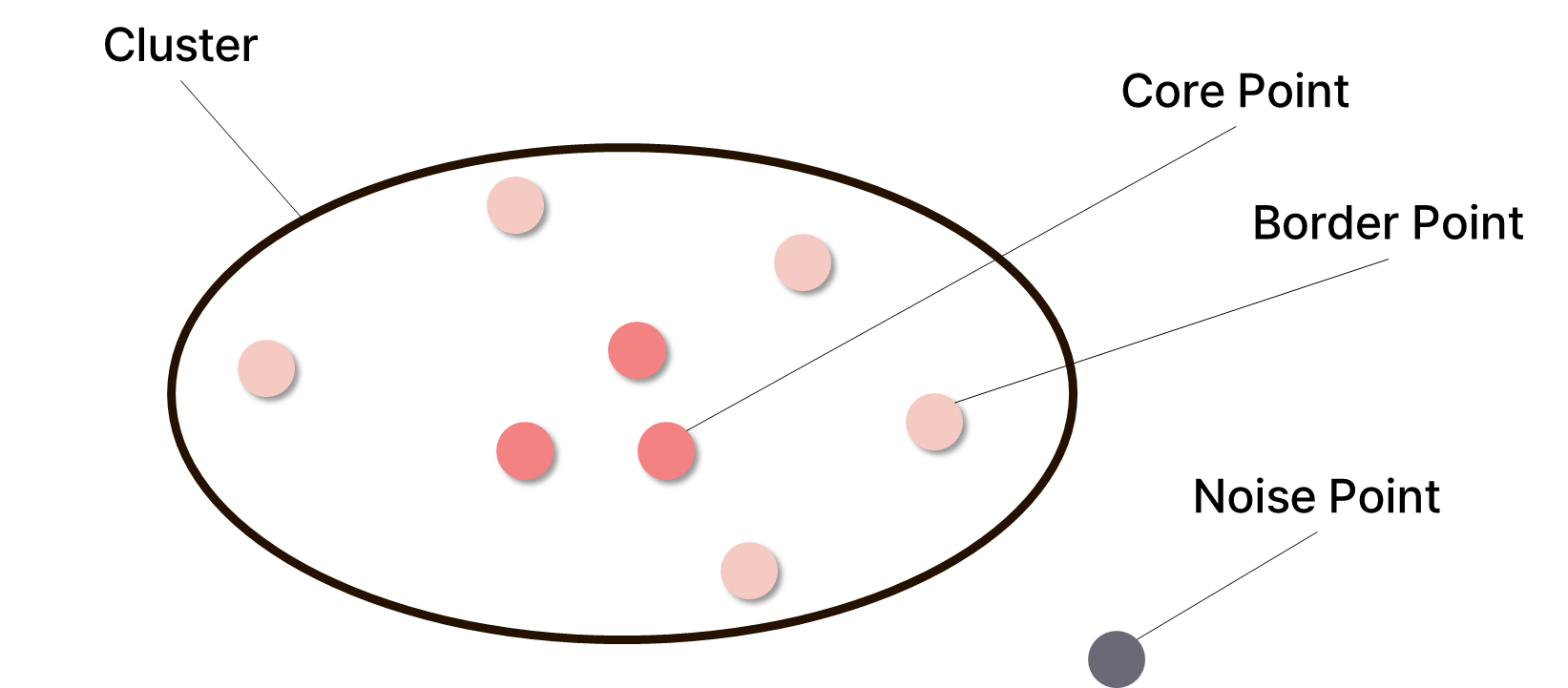
Core Point	epsilon 반경 내에 min_samples 이상의 데이터를 포함하는 군집의 중심점
Border Point	epsilon 반경 내에 min_samples 이상의 데이터를 포함하지 않지만, 해당 반경에 core point를 가지고 있는 점
Noise Point	epsilon 반경 내에 min_samples 이상의 데이터를 포함하지 않고, 해당 반경에 core point도 없는 점

그림참고

밀도 기반 군집화는 다음의 단계로 수행된다.

💡 밀도 기반 군집화 프로세스

1. 공간에서 임의의 점을 선택한다.
2. 앞 단계에서 선택한 임의의 점을 기준으로, epsilon 거리 범위 내에 있는 점의 개수를 센다.
   • 여기서 만약 점의 개수가 minpts-1 이상이면 해당 점을 core point로, 그렇지 않으면 noise point로 분류한다.
3. 앞 단계의 점이 core point가 되었다면, 해당 점을 기준으로 epsilon 범위 내에 있는 모든 데이터를 하나의 군집으로 지정한다.
   • 여기서 묶은 군집에 또 다른 core point가 속해 있다면, 그 점의 이웃 점들을 border point에 도달할 때까지 차례로 방문하여 군집에 포함시킨다.
4. 모든 데이터가 어떤 군집에 속하거나 혹은 noise point가 될 때까지 1-3을 반복한다.

scikit-learn 라이브러리를 사용하여 Python3으로 구현하면 다음과 같다.

from sklearn.datasets import make_blobs
from sklearn.cluster import DBSCAN
from pandas import DataFrame
import mglearn
import numpy as np

# Generate data samples
np.random.seed(1)
data, _ = make_blobs(n_samples=15, centers=3, cluster_std=0.8)

# Fit kmeans model
DBSCAN = DBSCAN(eps=3, min_samples=2)
DBSCAN.fit(data)

# Labels of each point
labels = DBSCAN.labels_ 
print('labels: ', labels) 

# Visualize clustering result
mglearn.plots.plot_dbscan()

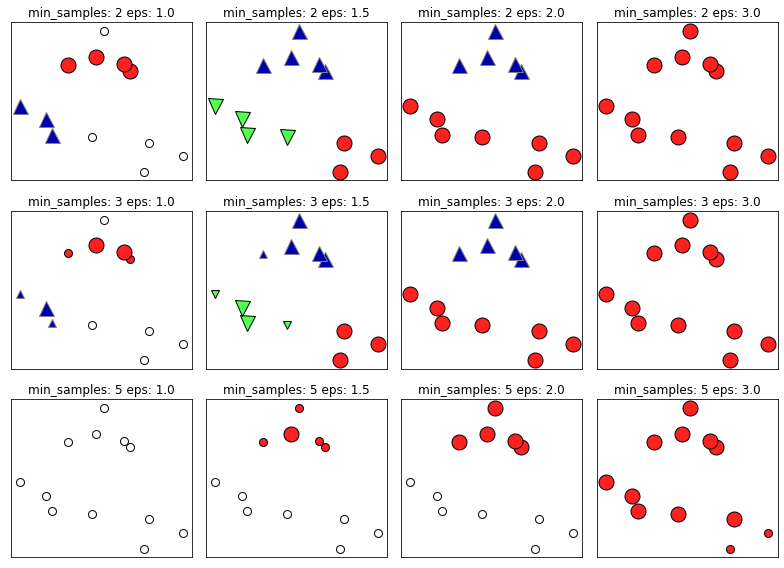DBSCAN 예제 결과

✅ DBSCAN 예제 결과 설명
core point는 크게, border point는 작게 표시되었으며, noise point는 흰색, 그 외에 군집에 속한 데이터 들은 색상이 칠해졌다. 해당 예시에서는 min_sample: 3, eps: 1.5가 데이터를 가장 잘 나눈 것으로 보인다.

4️⃣ 스펙트럼 군집화 (Spectral Clustering)

스펙트럼 군집화(Spectral Clustering)는 그래프 기반(graph-based) 군집화 기법으로, 데이터 간 절대적 거리를 기반으로 군집화를 수행하는 K-평균 군집화(K-means clustering), 계층적 군집화(Hierarchical clustering)와는 다르게, 데이터 간의 상대적 관계나 유사성을 고려하여 군집화를 수행한다.

💡 스펙트럼 군집화 프로세스

1. 주어진 데이터셋에서 데이터 점들 간의 관계를 정의한다.
   • 여기서 가중치는 데이터 간의 거리가 멀수록 커지고, 가까울수록 작아지도록 한다.
   • 보통 가우시안 커널을 사용하여 가중치를 정의한다.
2. 앞 단계에서 정의한(혹은 계산한) 값들을 바탕으로 인접 행렬(Adjacency matrix) 형태의 유사도 행렬(Affinity matrix)을 만든다.
   • 무방향 가중치 그래프(Undirected Weighted Graph) 형태로 볼 수 있다.
   • fully connected graph, k-nearest neighbor graph, ε-neighborhood graph 등 그래프를 만드는 여러 가지 방법들이 존재하며, 각 방법들이 가진 장단점이 다르므로 상황에 맞게 사용하도록 하자.
3. 만들어진 그래프에서 군집을 잘 나눌 수 있는 간선(edge)들을 선택하여 잘라낸다. (Fig C 참고)
   • 그래프를 자르는 방법으로 Minimum Cut이 보편적이며, 이 밖에도 Ratio cut, Normalized cut 등이 존재한다.
   • 그래프 컷은 각 방법에서 정의된 목적 함수(objective function)의 출력 값을 최소화하는 고유 벡터(eigenvector)를 찾아 이에 해당하는 가중치를 가진 간선들을 자르는 방식으로 수행된다.

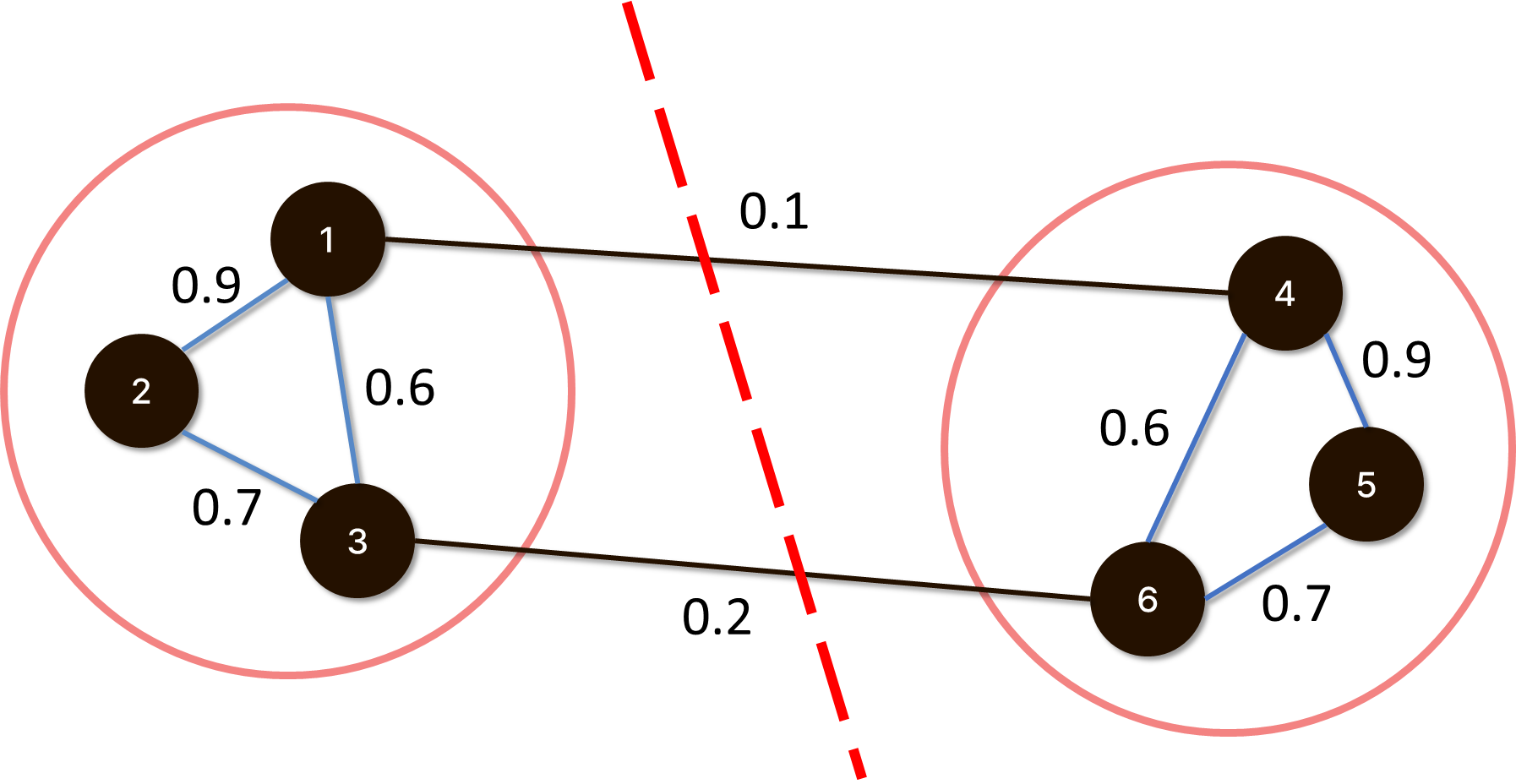Fig C. 그래프 컷 예시

scikit-learn 라이브러리를 사용하여 Python3으로 구현하면 다음과 같다.

from sklearn.datasets import make_circles
from sklearn.cluster import SpectralClustering, AgglomerativeClustering
import matplotlib.pyplot as plt

X, y = make_circles(n_samples=(250,500)
                                , random_state=3
                                , noise=0.04
                                , factor = 0.3)

fig, ax = plt.subplots(1,3, figsize=(15,4))

ax[0].scatter(X[:, 0], X[:, 1], alpha=0.7)
ax[0].set_title("Raw Data")

# Spectral clustering
pred = SpectralClustering(n_clusters=2
                            , eigen_solver="arpack"
                            , affinity="nearest_neighbors",).fit_predict(X)

ax[1].scatter(X[:, 0], X[:, 1], c=pred, cmap=plt.cm.rainbow, alpha=0.7)
ax[1].set_title("Spectral Clustering")

# Agglomerative clustering
pred = AgglomerativeClustering(n_clusters=2
                                  , linkage="ward").fit_predict(X)
ax[2].scatter(X[:, 0], X[:, 1], c=pred, cmap=plt.cm.rainbow, alpha=0.7)
ax[2].set_title("Agglomerative Clustering")

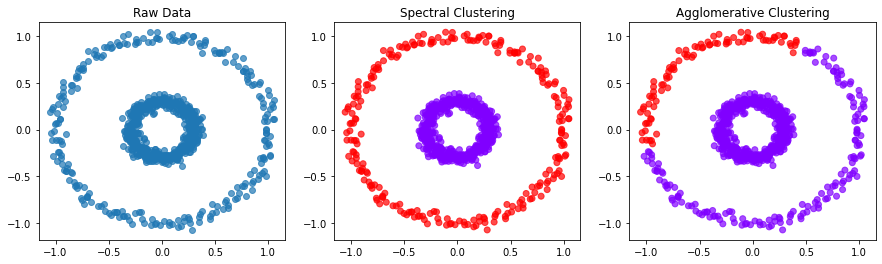Spectral Clustering과 합병에 의한 계층적 군집화(Agglomerative Clustering) 비교 예제 결과

---

References

고민삼,『Machine Learning』, 강의 교안.

ratsgo, "K-Nearest Neighbor Algorithm", Github.io, 2017.4.17
, https://ratsgo.github.io/machine%20learning/2017/04/17/KNN/

Tobigs, "클러스터링 실습 (1) (EDA,Sklearn)", Gitbook
, https://tobigs.gitbook.io/tobigs/data-analysis/undefined-3/python-2-1

조대협, "클러스터링 #3 - DBSCAN (밀도 기반 클러스터링)", Tistory, 2017.10.13 
, https://bcho.tistory.com/m/1205

Vibhor Agarwal, "Let’s cluster data points using DBSCAN", Medium, 2019.6.28 
, https://medium.com/@agarwalvibhor84/lets-cluster-data-points-using-dbscan-278c5459bee5

Satyam Kumar, "Hierarchical Clustering: Agglomerative and Divisive — Explained", Medium, 2020.8.3 
, https://towardsdatascience.com/hierarchical-clustering-agglomerative-and-divisive-explained-342e6b20d710

Zaid.Ryu, "[ML with Python] 3.비지도 학습 알고리즘 (3-3) DBSCAN", Github.io, 2020.12.26 
, https://jhryu1208.github.io/data/2020/12/26/ML_DBSCAN/