
1. 고유값과 고유벡터
1-1. 고유값과 고유벡터 정의
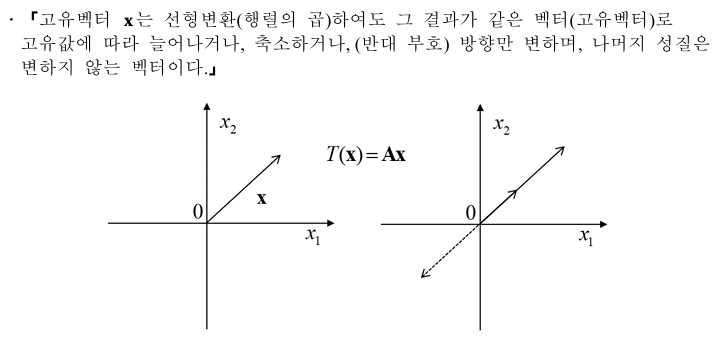
보통은 행렬 A가 벡터 x를 바꾸면, 벡터의 방향과 길이도 바뀐다. 그런데 특정한 벡터들은 방향이 안 바뀌고 길이만 λ배 바뀐다. 이렇게 방향이 안 바뀌는 벡터를 고유 벡터(Eigenvector)라고 하며, 이때 곱해진 숫자 λ를 고유값이라 한다.


고유값을 고유치라고도 하며, 고유벡터는 행렬의 곱에 의해 자기 자신의 상수배가 나오는 특별한 벡터이다. 고유값이 n개면 고유벡터도 무조건 n개가 나온다.
1-2. 고유값과 고유벡터 식 구하기
여기서 우리는 x = 0인 해에 관심이 없다. 모든 행렬에 대해 영 벡터를 넣으면 항상 성립하기 때문이다. 고유한 특징이 없기 때문에 우리는 x가 0이 아닌 해를 찾아 나선다.

자유 변수가 존재하면 해가 여러 개이고 무한히 많다는 뜻이기에, 0이 아닌 해도 존재한다는 것이다. 자유 변수가 있으려면 그 행렬은 역행렬이 없어야 하고, 역행렬이 없다는 것은 행렬식이 0이라는 뜻이 된다.


고유값이 여러 개 나오면 각각의 고유값을 다시 넣어서 풀면 그에 상응하는 고유벡터 x가 산출된다.
1-3. 고유공간
고유공간(Eigenspace)은 같은 고유값을 가지는 모든 고유벡터들의 모음 집합이다. 대신 0벡터는 제외한다.


1-4. 삼각행렬의 고유값
삼각행렬은 고유값을 쉽게 찾을 수 있는데, 바로 주대각선에 있는 숫자들이 고유값에 해당한다는 것이다. 그러므로 고유 방정식 없이도 고유값을 알 수 있게 된다.

1-5. 고유값이 0일 때
그리고 고유값이 0일 수도 있는데 고유값이 0이라는 것은 자유 변수가 존재한다는 뜻이며, 행렬 A가 역행렬을 갖지 않는다는 것을 의미한다.


행렬 A가 어떤 벡터 x를 완전히 짓눌러서 0으로 만든다. 이는 절대 뒤로 돌릴 수 없다는 뜻이기에 역행렬이 없다.
1-6. 고유벡터의 독립
서로 다른 고유값에 대응하는 고유벡터들은 항상 선형독립이다. 고유값이 서로 다르다는 말은 그에 대응하는 고유벡터들도 완전히 다른 방향을 가진다는 이야기이다.


고유값이 다르면 고유벡터도 서로 영향을 주지 않는다는 이야기가 되며, 결국 고유벡터들로 기저를 만들거나 대각화를 할 수 있게 된다.
