
1. 선형 방정식과 선형 변환
선형 방정식은 우리가 흔히 보는 식인 Ax = y이다. 여기서 A는 행렬, x는 입력 벡터, y는 출력 벡터이다. 이걸 함수로 보면 입력 x를 넣으면 결과 y가 나오는 것이라 볼 수 있다. 그래서 이걸 변환(Transformation) 또는 사상(Mapping)이라고 한다.

함수의 조건 중에 하나는 함수는 하나의 입력에 따른 하나의 출력이 있어야 한다고 정해져있다. 하지만 선형 변환에서는 한 입력이 여러 개의 출력으로 연결될 수 있기 때문에 변환이라고 말하는 것이다. (다차원 입력의 다차원 출력)
-
정의역(Domain) : 어떤 값을 넣을 수 있는 공간으로, 함수나 변환에 입력으로 들어갈 수 있는 모든 값들의 집합을 의미한다.
-
공변역(Codomain) : 함수나 변환을 거친 뒤 결과로 나올 수 있는 공간으로, 출력될 수 있는 값들의 집합을 의미한다.
1-2. 선형 변환
입력가 출력이 모두 벡터인 함수를 변환(Transformation)이라 한다. 그리고 n 차원에서 m 차원으로의 변환하는 것을 T: ℝⁿ → ℝᵐ 으로 표시하고, 각 벡터 x를 ℝᵐ의 하나의 벡터 T(x)에 할당한다.
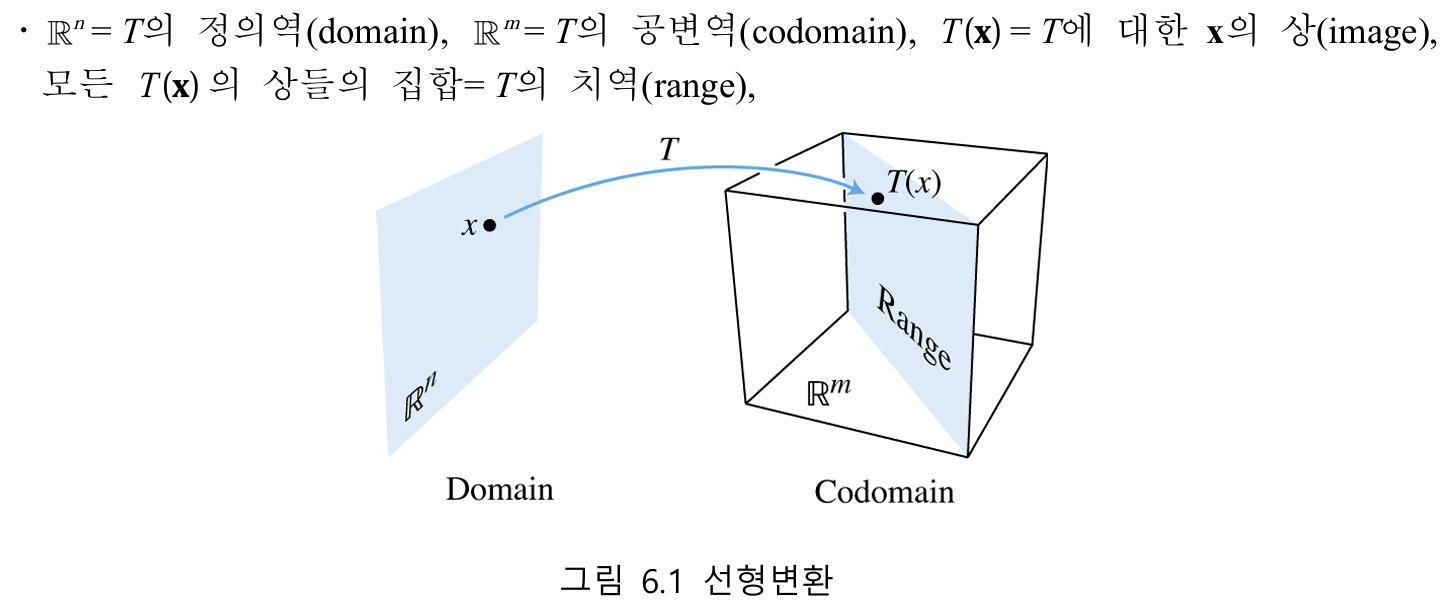



선형 변환(Linear Transformation)은 벡터의 덧셈 연산과 스칼라 곱의 연산에 닫혀있는, 벡터의 형태와 방향을 보존한 채로 바꾸는 변환을 말한다.

벡터 두 개를 더한 뒤 변환해도 각각 변환해서 더한 것과 결과가 같으며, 벡터에 어떤 수 k를 곱한 후 변환해도 변환 후에 k를 곱한 것과 값이 같다.

- 상(Image) : 어떤 입력 벡터가 선형 변환을 거쳐서 나오는 결과 벡터를 말한다. 상의 Image를 구하라고 하면 "변환 결과가 무엇인지 계산해봐라"라는 의미이다.
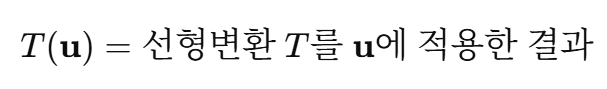
1-3. 행렬 변환
선형 변환은 결국 행렬 곱하기와 동일하다. 예를 들어, 벡터를 90도 회전시키거나 크기를 두 배로 늘리거나 반사시키는 등의 선형적인 변화는 전부 하나의 행렬로 표현할 수 있다. 그리고 행렬의 곱은 항상 선형 변환의 조건을 만족하기 때문에 모든 행렬 변환은 선형 변환이다.





여기서 행렬 A를 선형 변환 T에 대한 표준 행렬(Standard Matrix)이라고 한다.
1-4. 선형 변환의 기하학적 의미
선형 변환은 기준 축을 움직이는 것이라 보면 된다. 원래의 X축과 Y축이 변환되어서 기울어진 축이 되는 것이다. 그래서 그 기준 축으로 다시 표현하면 새로운 위치로 밀려나듯이 바뀌게 된다.
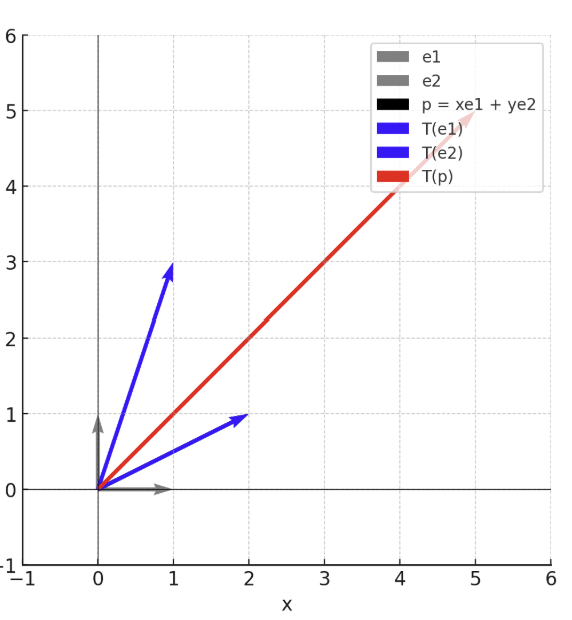
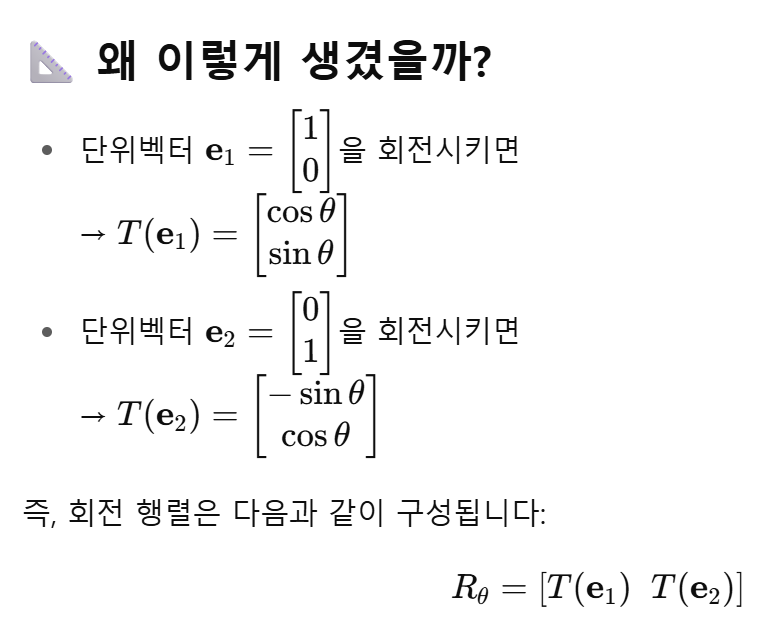
우리가 평면에서 어떤 벡터를 𝜃만큼 회전하는 것도 선형 변환이 된다. 덧셈, 스칼라 곱을 보존하기 때문이다. 정의역의 각 벡터가 선형 변환 후에도 길이와 벡터 사이의 각이 보존되며 방향만 바뀐다.


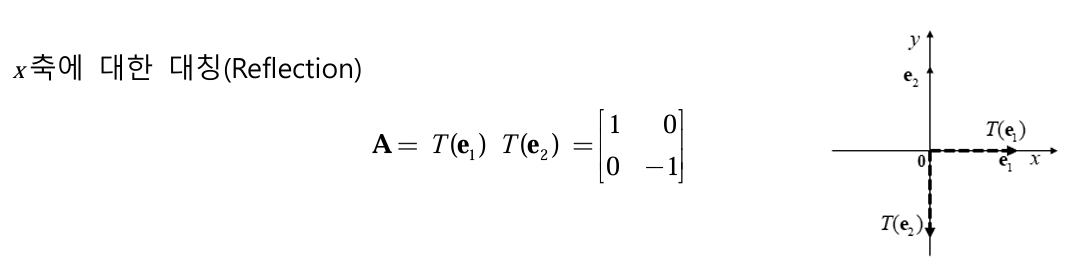
1-5. 선형 변환과 행렬식
선형 변환 T는 행렬 A로 표현되는데, 이 때 어떤 도형 S가 변환되면 그 도형의 넓이 또는 부피가 det(A)의 절댓값 배로 바뀐다.


절댓값을 씌우는 이유는 넓이나 부피는 항상 양수이기 때문에, 부호를 빼고 크기만 계산하는 것이다. det(A)의 값이 0보다 작다면 방향이 뒤집혔다는 의미가 된다.

2. 전사 및 일대일 변환
2-1. 전사 변환
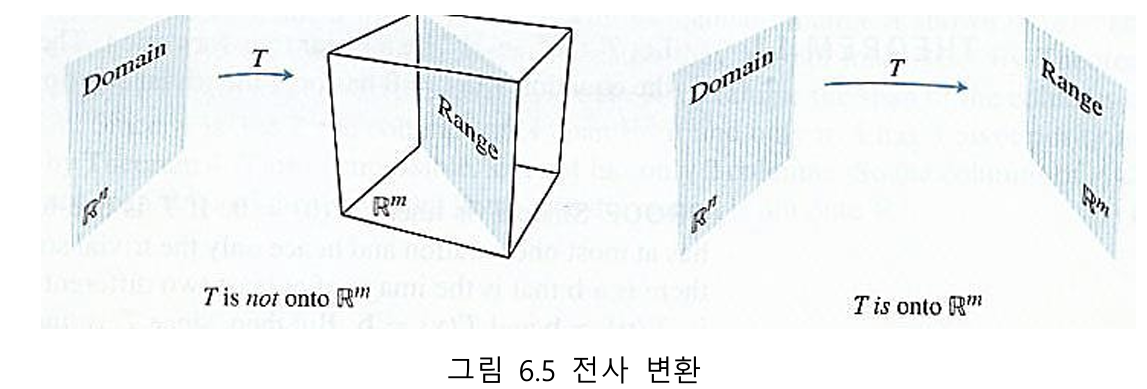
전사 변환(Onto Mapping)은 출력 공간의 모든 벡터가 선형 변환으로 만들어질 수 있는지를 보는 것이다. T(x) = b의 해가 언제나 존재하면 전사라고 할 수 있다. 즉, 아무 벡터 b를 찍어도 그걸 만들어내는 x가 최소 하나는 항상 존재한다는 뜻이다.


전사 변환에서는 Ax = y일 때 y를 이용해서 x를 구할 수 있게 된다. 정의 구역의 모든 데이터가 치역이 된다고 생각하면 편하다.
2-2. 일대일 변환
어떤 출력값 b에 대해 단 하나의 입력값 x만 존재하는 것을 일대일 변환(One-to-one Mapping)이라고 한다. 일대일 변환은 단사 변환이라고도 말하는데, 쉽게 말하면 결과가 같으면 원인도 같아야 한다는 것이다.
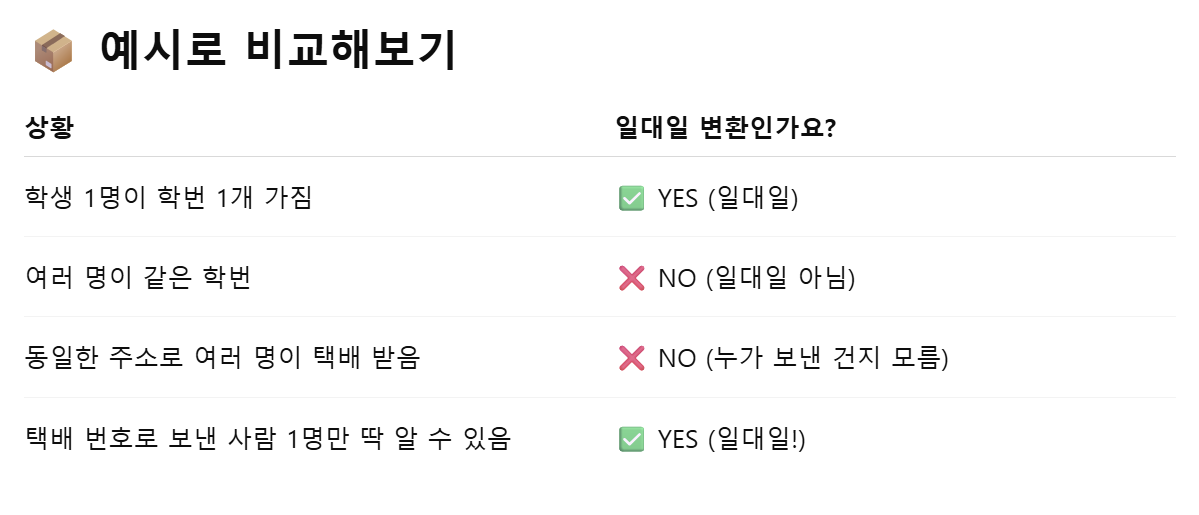
M 차원의 각 b에 대해 T(x) = b의 해는 유일하거나 없다. (= 해가 많아야 1개이다.) 선형 변환 T가 일대일 변환한다는것은 선형 방정식의 해가 유일하다는 것을 의미한다.
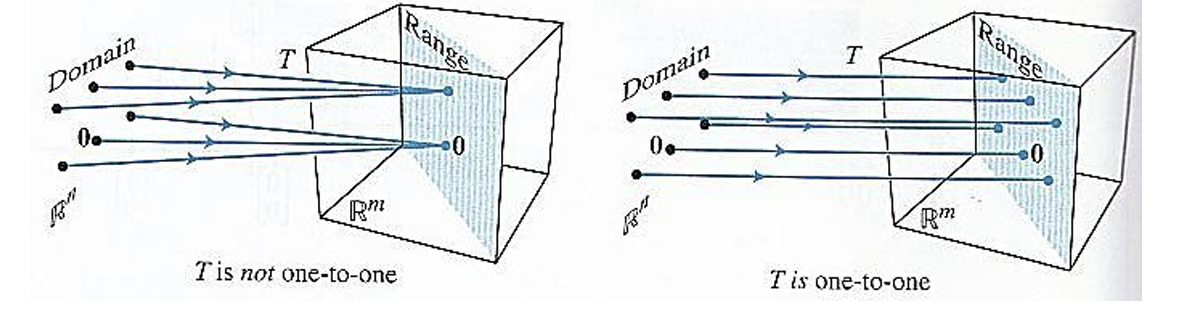

일대일 변환의 필요 충분 조건은 동차 선형 방정식 T(x) = 0이 자명한 해(x = 0)만 가져야 한다는 것이다.
전사 변환은 열 벡터들을 조합해서 m 차원의 어떤 벡터든 만들 수 있어야 하고, 일대일 변환은 행렬 A의 열 벡터들이 일차 독립이어야 한다.


전사는 열 벡터들이 넓게 퍼져서 전체 공간을 채우는 것이고, 일대일 변환은 열벡터들이 겹치지 않게 독립적으로 있는 것이다.
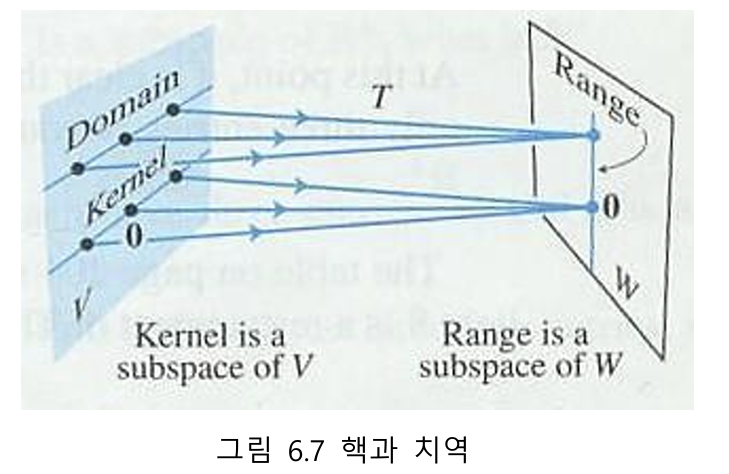
3. 선형 변환(사상)의 핵과 치역(상)
- 핵(Kernel), 영공간(Null space) : 결과가 0이 되는 입력들만 모아둔 공간이다. 변환했더니 0이 되어버리는 벡터들만 모아놓은 곳이라 보면 된다.

- 치역(Image), 상공간(Range space) : 변환을 거쳐 실제로 나오는 결과들만 모은 공간이다. 변환을 했더니 실제로 만들어진 결과 벡터들만 모은 곳이라 보면 된다.

일대일 여부를 살펴 볼 때는 Kernel에 아무 것도 없어야 하며, 전사 여부를 살펴 볼 때는 Image가 전체 공간을 덮어야 한다.

A가 가역 행렬이라는 것은 역행렬이 존재한다는 것이고, 어떤 결과 Ax = b에 대해 항상 유일한 해 x를 구할 수 있다는 것이다. T가 전사 변환이라는 것은 n차원의 모든 벡터가 변환 결과로 나올 수 있다는 것이다. T가 일대일 변환이라는 것은 결과가 같으면 입력도 같아야 한다는 것이다.


