[2025-1학기] 선형대수학 - 기저, 차원, 계수

1. 기저

• 기저(Basis) : 해당 공간의 기준점이 되는 부분이다.

하나의 벡터공간에 기저가 될 수 있는 집합은 여러 개가 있을 수 있다. 그러나 그 벡터공간의 기저를 이루는 집합들의 각 원소의 개수는 모두 같다.

차원은 기저의 개수와 동일하다.

• 표준 기저(Standard Basis) : 각 좌표축을 따라 하나만 1이고 나머지는 전부 0인 기본적인 기저를 말한다.

1-1. 기저의 생성

1-2. 널공간의 기저

해를 매개 벡터 형식으로 표현하는 것이 중요하다. 자유변수 자체는 벡터가 아니지만, 각 자유변수를 1로 두고 만든 해 벡터들이 널 공간의 기저를 이루는 선형독립한 벡터가 되기 때문이다.

1-3. 열공간의 기저

사다리꼴로 변형했을 때 오리지널 컬럼이 기저를 이룬다는 것을 잊지 말아야 한다.

1-4. 행공간의 기저

여기서 약간 혼동이 올 수 있는데, 열공간의 기저는 원래 행렬 A의 피봇 열들을 그대로 가져오면 된다. 하지만 행공간의 기저는 기약 사다리꼴에서 0이 아닌 행들을 가져오면 된다.

2. 차원

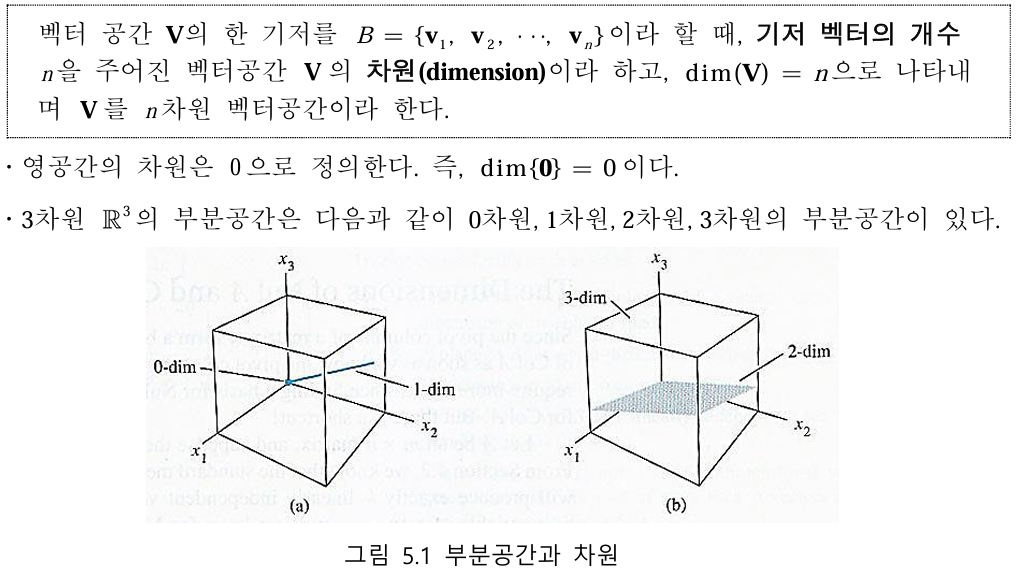
2-1. 널공간과 열공간의 차원

3. 계수

계수(Rank)는 그 행렬이 표현할 수 있는 선형적으로 독립한 방향(벡터)의 수이다. 선형독립한 행 또는 열의 수이자, 축약 사다리꼴에서 pivot의 개수와 동일하다.

3-1. 계수의 성질

3-2. 정칙행렬의 기저와 계수

3-3. 계수와 해의 존재

rank에 따라서 해가 존재하는지를 살펴본 것이다.

4. 행렬의 차원 정리

여기서 rank(A)는 기본변수의 개수, dim(Nul(A))는 자유변수의 개수라고 생각하면 쉽다.