
1. 벡터공간
벡터공간은(Vector Space)은 영벡터를 포함해야 하며, 덧셈과 스칼라 곱을 자유롭게 할 수 있어야 한다.

2. 부분공간
벡터공간 V에서 V 자신과 {0}은 V의 부분공간들 중 하나이다. 이러한 부분공간을 V의 자명한 부분공간(Trivial Subspace)라고 하며, 특히 {0}을 영공간(Zero Space)라고 한다.

부분공간이 되기위해서는 영벡터를 포함해야 한다. 그리고 "~에 닫혀있다"는 말은 어떤 집합 내에 존재한다는 것을 의미한다.
3. 선형결합과 부분공간

부분 공간인지 아닌지 확인하고자 한다면 다음 조건을 만족해야 한다.
-
영벡터를 포함하고 있어야 한다.
-
벡터 덧셈에 닫혀 있어야 한다.
-
스칼라 곱에 닫혀 있어야 한다.
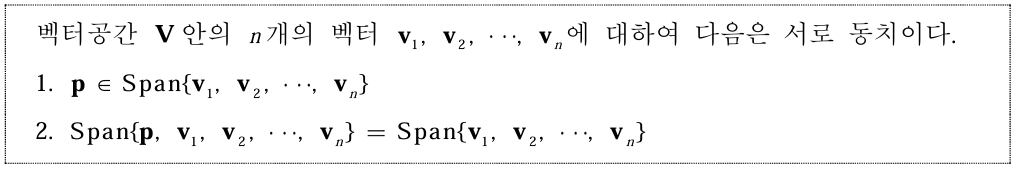
4. 널공간
m × n 행렬 A의 널공간(Null Space)은 동차선형방정식의 해 합이며, Nul(A)로 나타낸다. Nul(A)는 n차원의 벡터 공간의 부분공간이다.
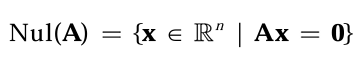
영공간이라 부르기도 하는데, 영벡터만으로 이루어진 벡터공간 {0}과 혼동할 수 있어 영화공간이라고도 한다.
널공간은 벡터공간을 이룬다. 참고로 비동차선형방정식의 해 집합은 벡터공간을 이루지 못한다.
4-1. 널공간의 성질

5. 열공간
m × n 행렬 A의 열공간(Column Space)은 A의 열벡터들의 모든 선형결합의 집합이며, Col(A)로 나타낸다. 열벡터로 만들 수 있는 모든 선형결합이 열공간이다.

5-1. 열공간의 성질

자유변수가 없는 열 즉, 피봇열에 해당하는 열벡터만 뽑아서 열공간의 기저로 나타낼 수 있다.
5-2. 널공간과 열공간의 비교
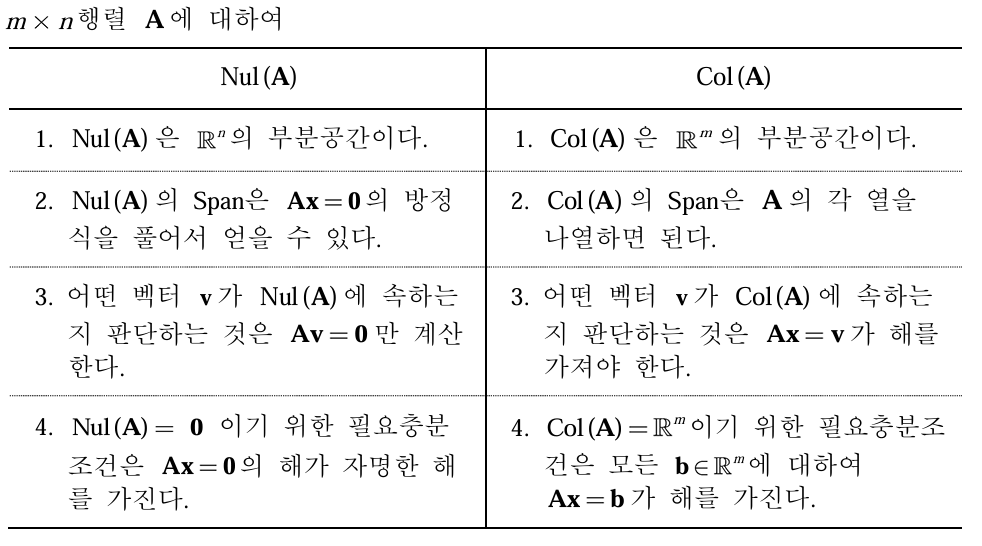
널공간은 행렬 A에 어떤 벡터를 곱하니 결과가 0이 되는 경우를 모은다.
6. 행공간
m × n 행렬 A의 행공간(Row Space)은 A의 행벡터들의 모든 선형결합의 집합이며 Row(A)로 나타낸다.

6-1. 행공간의 성질

가우스 소거로 피봇이 있는 행의 행 번호를 먼저 찾는다. 그리고 원래 행렬로 돌아와 그 행 벡터만 뽑아서 사용하면 행공간을 Span으로 나타낼 수 있다.
6-2. 행공간과 널공간의 관계

