
1. 기저와 좌표
우리는 평면에서 (3, 2)을 보통 x축 1칸, y축 1칸 기준으로 본다. 나만의 새로운 축을 만들어서 그 축을 기준으로 벡터를 표현하면 좌표가 달라지는 것은 당연하다. 여기서 그 기준이 되는 축이 바로 기저(Basis)이다.

기저 B가 표준 기저(가장 기본적으로 사용하는 기저)일 경우, 기저 B를 생략할 수 있다. [X] = X가 된다. 또한, 동일한 벡터일지라도 기저가 다름에 따라 좌표가 달라진다.

1-1. 좌표 변환
-
x: 원래 벡터 (예 : (3, 2) 같은 거) -
[𝑥]𝐵: 기저 B 기준 좌표 (벡터가 기저 B를 기준으로 얼마나 조합됐는지를 숫자로 표시) -
PB: 기저 B의 벡터들을 열벡터로 놓은 행렬(예 : 기저 B = {𝑏1, 𝑏2}라면 𝑃𝐵=[𝑏1 𝑏2])
[기저 B 기준 → 표준 기저 기준]


[표준 기저 기준 → 기저 B 기준]


PB는 기저 B에서 표준기저로 좌표를 바꿔주는 좌표 변환 행렬이다. 기저 벡터들을 열 벡터로 가지며, 가역 행렬이다. 기저는 선형 독립이라 열 벡터들이 선형 독립이고, 그 기저 벡터들로 공간 전체를 표현할 수 있어 항상 역행렬이 존재한다.
P B−1은 표준 기저에서 기저 B로의 좌표 변환 행렬이며, 좌표 사상(Coordinate mapping)이라고도 한다.
1-2. 좌표 변환 행렬
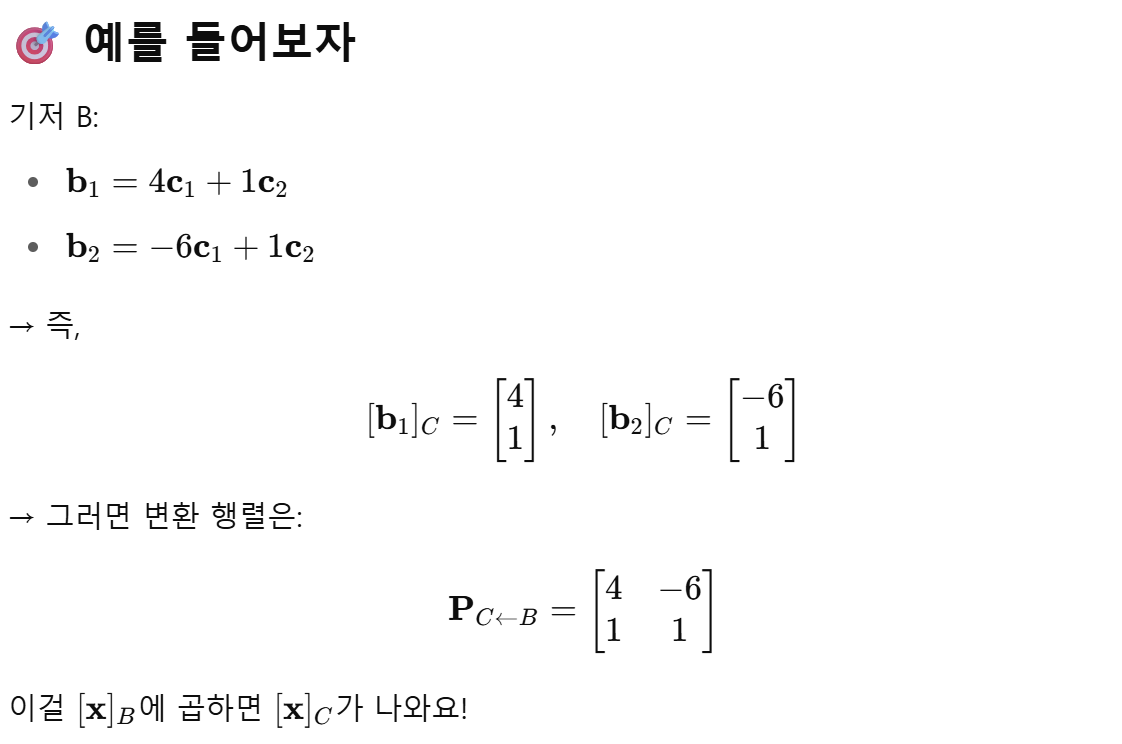
변환 행렬은 같은 벡터라도 기저마다 좌표를 나타내는 것이 다르기 때문에, 어떤 기준의 좌표를 어떤 기준의 좌표로 바꾸기 위해 알려주는 역할을 수행한다. [x]C = P C←B [x] B는 벡터 X의 기저 B 기준 좌표를 알고 있다면, 그것을 기저 C 기준으로 바꾸고 싶을 때 이 변환 행렬을 이용하면 된다는 이야기이다.

변환 행렬은 B의 기저 벡터들을 C 기저 기준 좌표로 나타내고 열 벡터로 붙여서 만든 행렬이다. 변환 행렬은 일차 독립(겹치지 않고 서로 독립적)이므로 역행렬이 항상 존재한다.
가우스 소거법을 활용한 좌표 변환 행렬 구하기


여기서 왼쪽에는 C의 기저 벡터, 오른쪽에는 B의 기저 벡터를 두고 왼쪽 행렬을 단위 행렬로 만들면 오른쪽이 기저 B를 기저 C로 만드는 변환 행렬이 된다.
표준 좌표로 변환시킨 후 좌표 변환 행렬 이용하기
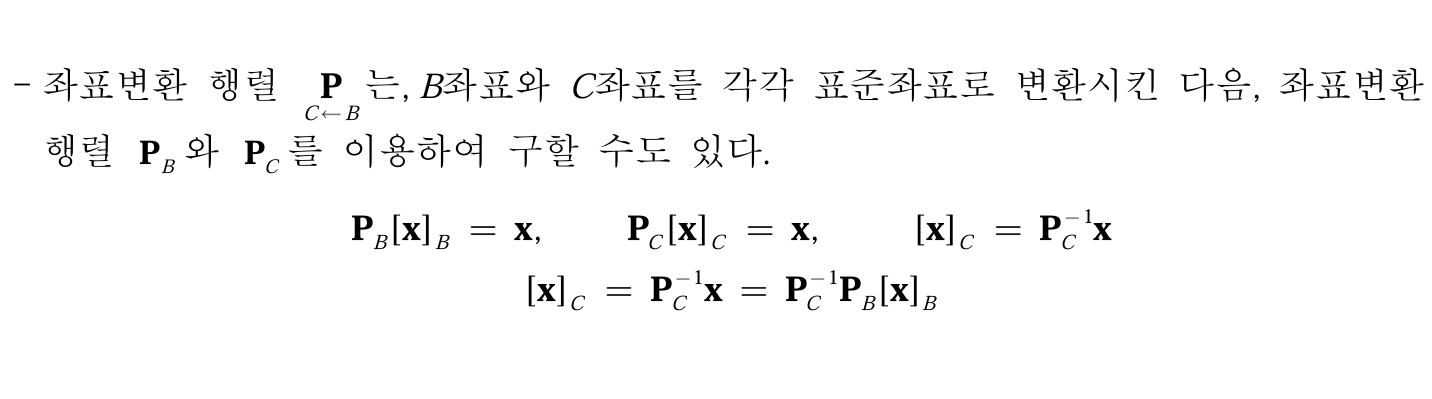
예를 들어, B 기저 좌표에서 C 기저 좌표로 바꾸고 싶을 때 굳이 직접 변환하지 않아도 표준 기저(기본 좌표계)를 중간에 거치면 더 쉽게 구할 수 있다.



