
1. 내적
내적은 두 벡터가 얼마나 같은 방향을 향하고 있는지를 숫자로 말한 것이다. 우리는 내적을 공부할 때 서로 얼마나 같은 방향인지를 잘 살펴보고, 성분끼리 곱해서 더해야 한다.

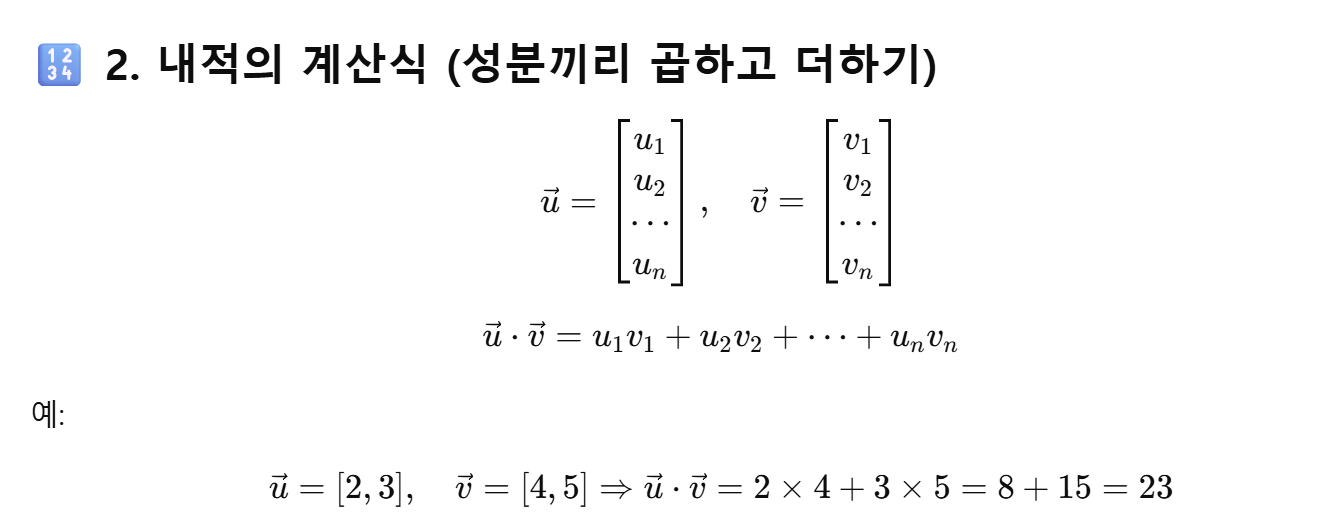
내적(Inner Product)과 도트 곱(Dot Product) 그리고 스칼라 곱(Scalar Product)는 동일한 표현이다.
2. 직교
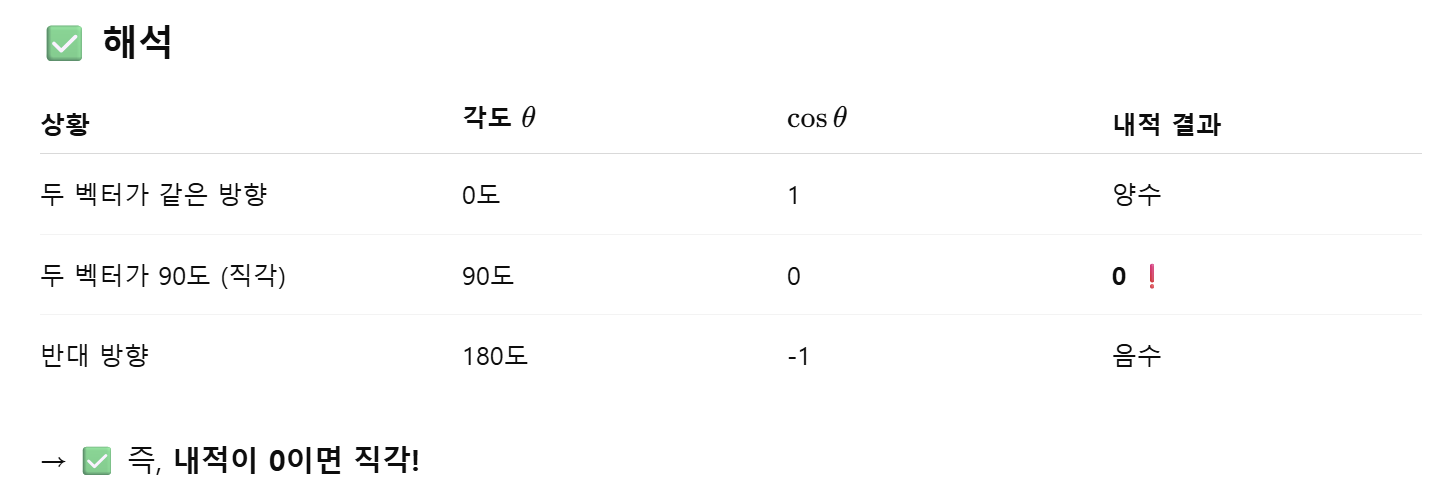
두 벡터의 내적이 0이면 두 벡터는 직교(= 서로 직각)한다고 말한다. 두 벡터 사이의 각도가 90도(직각)이라는 뜻이다.
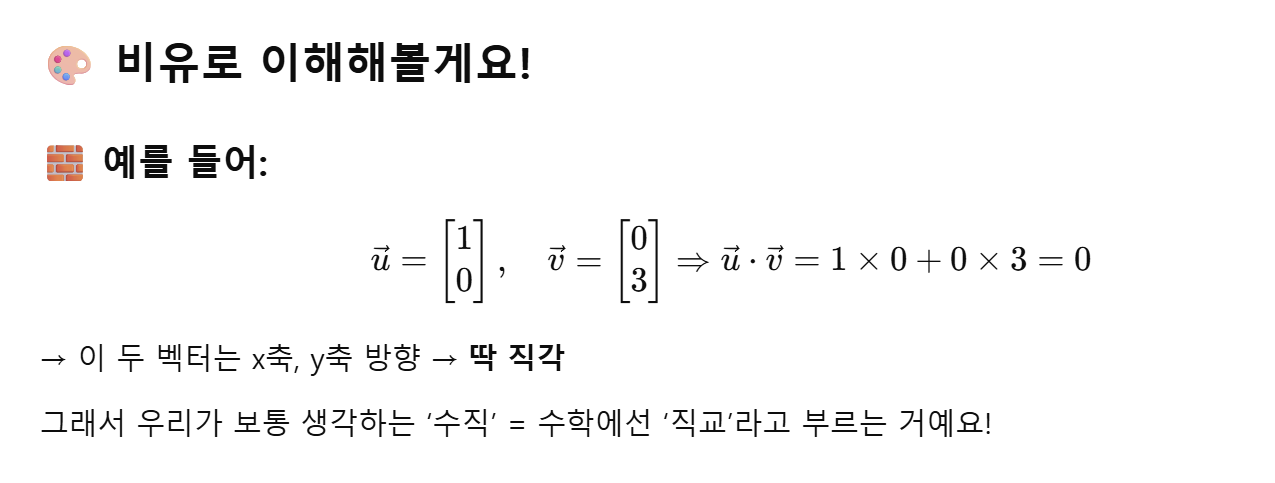

참고로 영 벡터는 길이가 0이고 방향이 없다. 어떤 벡터랑 곱하든지 다 0이 되기 때문에 모든 벡터와 직교한다고 보는 것이다.
2-1. 직교 여공간
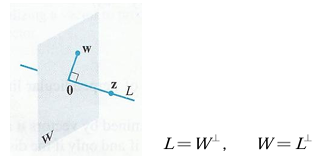
직교 여공간(Orthogonal Complements)은 어떤 공간 W가 있을 때 W에 있는 모든 벡터와 직각(직교)을 이루는 벡터들을 모아서 만든 공간을 의미한다.


2-2. 직교 집합
직교 집합(Orthogonal Set)은 벡터 집합 안에서 서로 다른 두 벡터끼리 내적이 0인 것을 말한다. 벡터들끼리 전부 직각(= 직교)이고, 하나 하나 서로 간섭하지 않고 완전히 다른 방향을 가리킨다.
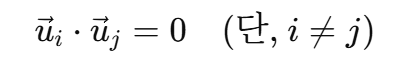

2-3. 직교 기저
직교 집합이 선형 독립까지 만족하면 이 집합은 어떤 부분 공간의 기저가 될 수 있다. 이를 직교 기저(Orthogonal Basis)라고 말한다.


참고로 두 벡터의 직교는 두 벡터의 독립을 의미한다.
3. 정규 직교 집합과 정규 직교 기저
정규 직교는 서로 직각이면서 길이가 1인 벡터들을 말한다. 정규 직교 집합(Orthonormal Set)은 서로 직각이어야 하며, 각 벡터의 크기가 1인(단위벡터) 벡터들이 모인 집합을 의미한다.
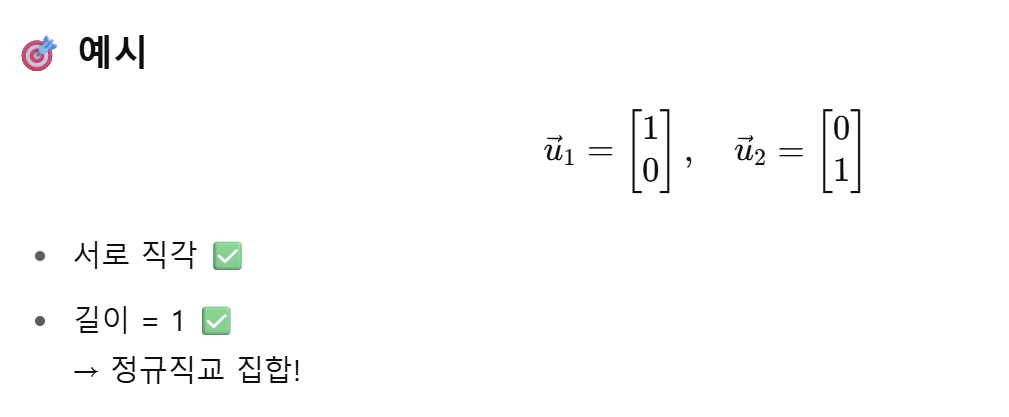
만약 정규 직교 집합이 어떤 공간 전체를 만들어낼 수 있다면(= Span으로 기저가 된다면) 그것을 정규 직교 기저(Orthonormal Basis)라고 한다.
4. 열벡터가 정규 직교 집합인 행렬의 성질





5. 직교 행렬
직교 행렬(Orthogonal Matrix)은 열 벡터들이 정규 직교인 행렬이고, 전치 = 역행렬이 되는 아주 특별한 행렬을 말한다. 길이, 각도, 직각 관계를 그대로 유지하면서 벡터를 변환할 수 있다.


좀 쉽게 생각하면, 서로 직각이고 길이가 1이라면 정규 직교 집합을 이루게 되는데, 이런 벡터들로 만든 행렬이 직교 행렬인 것이다.
