
1. 대각화
어떤 행렬 A가 있을 때 그것과 비슷한 모습이지만 더 단순한 대각 행렬 D로 바꿀 수 있다면, 우리는 A를 대각화할 수 있다고 말한다.
행렬 A가 어떤 복잡한 기계라고 가정하고, 이 기계는 어떤 숫자 혹은 벡터를 입력하면 복잡한 방식으로 바꾸는 역할을 수행한다. 근데 이 복잡한 기계를 더 단순한 형태로 바꿔서 더 쉽게 계산할 수 있도록 해주는 것이 대각화이다.


어떤 정방 행렬 A가 있을 때 그 행렬이 서로 다른 방향의 고유 벡터 n개를 가지고 있다고 하면 우리는 A를 대각화할 수 있다. 즉, 고유 벡터가 충분히 많고 서로 독립적이면 대각화가 가능하다.

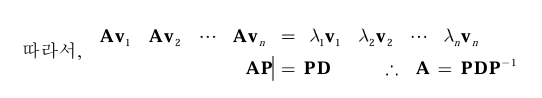
1-1. 대각화의 충분 조건
n차 정방 행렬 A의 고유값이 모두 다르다면 각 고유값에 대응하는 고유 벡터의 집합은 선형 독립이다. 따라서 A는 대각화가 가능하다. 즉, n개의 서로 다른 실수를 고유값으로 갖는 n차 정밥 행렬은 대각화가 가능하다.
물론 고유값이 서로 다르지 않아도(= 중복된 고유값이 있어도) 고유 벡터들이 선형 독립이면 대각화가 가능하다.






2. 고유합
고유합 또는 대각합(Trace)은 어떤 행렬의 대각선 성분들만 더한 값을 말한다.

행렬을 더한 후 고유합을 구하는 것은 각각의 고유합을 구해서 더한 것과 동일하다. 또한, 두 행렬을 곱한 후 고유합을 구할 때 곱하는 순서를 바꿔도 고유합은 동일하다.

고유합과 곱의 관계는 다음과 같다.

3. 선형 변환의 고유값, 고유 벡터


벡터 공간을 자기 자신으로 바꾸는 변환이 있고 이 변환이 행렬 A로 표현된다면, 이때 행렬 A의 고유값은 선형 변환 T의 고유값이고, 행렬 A의 고유 벡터는 선형 변환 T의 고유벡터이다.



4. Cayley-Hamilton 정리
행렬 A에 대해서 만든 고유 방정식(특성 방정식)에 고유값 대신 그냥 행렬 A를 넣어도 등식이 성립하는 정리이다. 즉, 모든 정방 행렬은 자기 자신의 고유 방정식을 만족한다.

모든 정방 행렬의 역행렬은 행렬의 거듭 제곱의 합으로 나타낼 수 있게 된다.

5. 고유값과 고유 벡터의 관계
A가 n차 실수 정방 행렬일 때, 다음과 같은 관계를 가진다.
- 고유값은 실수일 수도 있고 복소수일 수도 있다. 실수 행렬이라도 고유값이 복소수로 나올 수 있기 때문이다.

-
고유값이 실수냐 복소수냐에 따라서 고유 벡터도 성질이 달라진다. 고유값이 실수면 고유 벡터도 실수 성분만 가질 수 있고, 고유값이 복소수이면고유 벡터도 복소수 벡터가 된다.
-
고유값이 서로 다르면 고유벡터도 독립적이다. 즉, 대각화가 가능하다.

- 고유값에 0이 있으면 역행렬이 없다.





결국 고유 벡터는 행렬을 어떻게 바꿔도 그대로이고, 고유 값만 역수, 빼기, 곱하기, 제곱 등으로 규칙적으로 바뀐다.
