
1. 동차선형방정식
동차(질)연립일차방정식(Homogeneous System of Linear Equations) : 선형방정식에서 b=0인 방정식을 말한다.
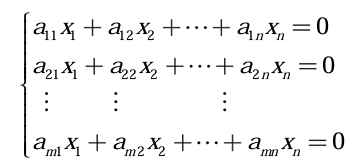
동차선형방정식은 오른쪽의 상수항(절편값)이 모두 0이다. 항상 해가 존재하며, 상수항이 0이 아닌 방정식은 비동차선형방정식(Nonhomogeneous System of Linear Equation)이라 한다.
동차선형방정식은 항상 0인 해를 갖기 때문에, 적어도 하나 이상의 해가 반드시 존재한다. 전체 해가 0인 것을 자명한 해(Trivial Solution)이라고 하고, 자명하지 않은 해가 존재한다면 자명하지 않은 해(Nontrivial Solution)이라 한다.


동차선형방정식은 해가 무조건 존재한다. 다만 여기서 팁이 있다면, 미지수의 개수가 방정식의 개수보다 많다면 자명하지 않은 해가 있을 가능성이 매우 높다.
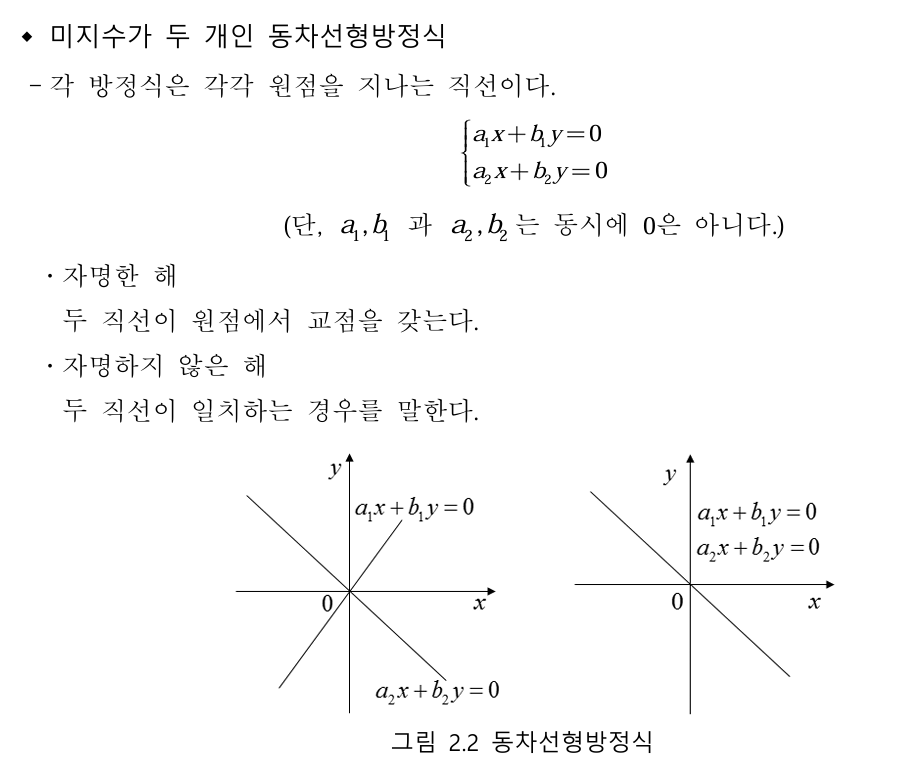
동차선형방정식은 각 방정식에서 변수들의 값이 0일 때 해가 되는 특성을 공통적으로 갖고 있어 동차선형방정식이라 한다.
2. 선형방정식과 역행렬
선형 방정식 Ax = b가 유일한 해를 가질 때, A의 역행렬을 구하고 이것을 이용해서 해를 구할 수 있다.
참고로 역행렬은 기본행 연산을 통해서, 혹은 여인수 전개를 통해서 구할 수 있다.
2-1. 기본행렬
기본행렬(Elementary Matrix)는 단위행렬 I에 기본행 연산을 한 번 적용해서 만든 행렬이다.

기본행렬은 항상 정칙이기 때문에 역행렬이 존재한다. 역행렬도 기본행렬이며, 행 연산을 행렬곱으로 표현할 수 있어 가우스 소거법에서 유용하다.

2-2. 정칙행렬의 성질
정칙행렬은 역행렬이 존재하는 정방행렬을 말하며, 정방행렬은 행과 열의 수가 동일한 행렬을 뜻한다. 정칙행렬의 성질은 다음과 같다.

