
1. 사다리꼴 행렬
사다리꼴 행렬(Row Echelon Form Matrix)은 다음과 같은 모양과 특징을 가진 행렬이다.

-
모든 원소가 0으로 구성된 행은 맨 아래의 행에 위치시킨다.
-
임의의 연속된 두 행에 대하여, 밑에 있는 행의 선두 운소는 위에 있는 행의 선두 원소보다 오른쪽에 놓여야 한다.
-
선두 원소가 있는 열에서 선두 원소 아래에 있는 모든 원소는 0이다.
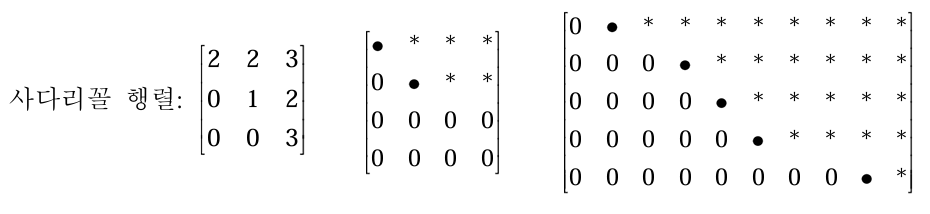
선두 원소(Leading Entry)란 한 행의 가장 왼쪽에 있는 0이 아닌 원소를 의미한다. 그러므로 각 행의 선두 원소는 항상 존재한다.
2. 축약 사다리꼴 행렬
사다리꼴 행렬이 다음 조건을 만족하면 축약(기약) 사다리꼴 행렬(Reduced Row Echelon Form)이 된다. 여기서 '기약'의 의미는 더 이상 줄어들지 않는다는 의미이다.
-
사다리꼴 행렬의 1, 2, 3 조건을 모두 만족한다.
-
각 행의 선두 원소는 1이다.
-
선두 원소가 있는 열에서 선두 원소만 1이고 나머지는 0이다.
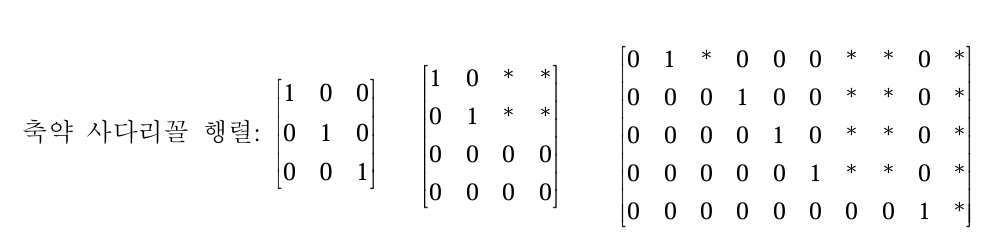
사다리꼴 행렬에서는 각 선두 원소 아래에 있는 수가 0이지만, 축약 사다리꼴 행렬에서는 각 선두 원소 아래뿐만 아니라 위에 있는 원소도 0이다.
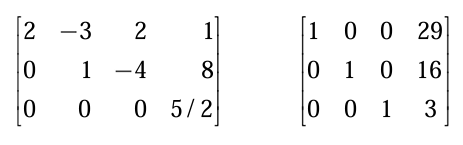
기본행 연산을 유한 번 사용하면 임의의 행렬을 사다리꼴 행렬과 축약 사다리꼴 행렬로 만들 수 있다. 왼쪽은 사다리꼴 행렬이고, 오른쪽은 축약 사다리꼴 행렬이다.
3. 가우스 소거법, 가우스-조르단 소거법
임의의 행렬에 대하여 기본행 연산에 의하여 얻어진 사다리꼴 행렬은 그 모양(원소값)이 다양하다. 그러나 추가적인 기본행 연산에 의해 얻어진 축약 사다리꼴 행렬은 유일하다.
임의의 행렬을 사다리꼴 행렬로 변형하는 방법을 가우스 소거법(Gaussian Elimination)이라 하고, 다시 축약 사다리꼴 행렬로 변형하는 방법을 가우스-조르단 소거법(Gauss-Jordan Elimination)이라 한다.
4. 피봇
-
피봇(Pivot) : 행렬을 (축약) 사다리꼴로 변환했을 때 선두 원소의 위치를 의미한다.
-
피봇열(Pivot Column) : 피봇 위치에 해당하는 열을 의미한다.
동일한 행렬에 대한 사다리꼴 행렬의 형태가 다를지라도 선두 원소의 위치는 항상 같은 자리이다.
피봇이란 기본행 연산의 치환에서 다른 행의 원소를 0으로 만들기 위해서 사용되는 0이 아닌 원소의 위치(값)을 의미한다.

확대행렬을 사다리꼴 행렬로 바꾼 다음, 축약 사다리꼴 행렬로 바꾸면 해 집합을 구할 수 있다.
축약 사다리꼴 행렬은 각 피봇이 1이어야 하며, 각 피봇이 있는 열의 나머지 원소는 0이어야 한다.
참고로, 같은 행렬이 주어졌을 때 사다리꼴 행렬과 축약 사다리꼴 행렬의 피봇 위치는 동일하다. 축약 사다리꼴 행렬은 더 간단한 형태일 뿐이라서 그렇다.
4. 행 축약 알고리즘
-
가장 왼쪽의 0이 아닌 열을 찾고, 이 열을 피봇열로 정한다.
-
피봇열에서 0이 아닌 원소를 피봇으로 선택한다. 이 때 행의 교환이 가능하다.
-
선택한 피봇열의 피봇 아래에 있는 모든 원소를 0으로 만들기 위해 행 치환을 수행한다.
-
선택한 피봇과 그 위에 있는 모든 행은 다음 단계에서 제외한다. 남아있는 행에 대해 더 이상 수행해야 할 행이 없을 때까지 이 과정을 반복한다.
-
(축약 사다리꼴 행렬 생성) 가장 오른쪽에 있는 피봇을 선택하여 위쪽과 왼쪽 방향으로 각 피봇의 위에 있는 원소를 0으로 만들기 위해 행 치환을 수행한다. 그리고 각 피봇의 값이 1이 아니면, 1로 만들기 위해 상수배를 수행한다.
5. 해 집합의 표현
-
기본 변수(Basic Variable) : (축약) 사다리꼴 행렬에서 피봇열에 대응하는 변수를 말한다.
-
자유 변수(Free Variable) : 기본 변수 외의 변수들을 말한다.
여기서 자유라는 말은 우리가 변수의 값으로 임의의 값을 선택할 수 있다는 것을 의미한다. 즉, 실수 값이다.
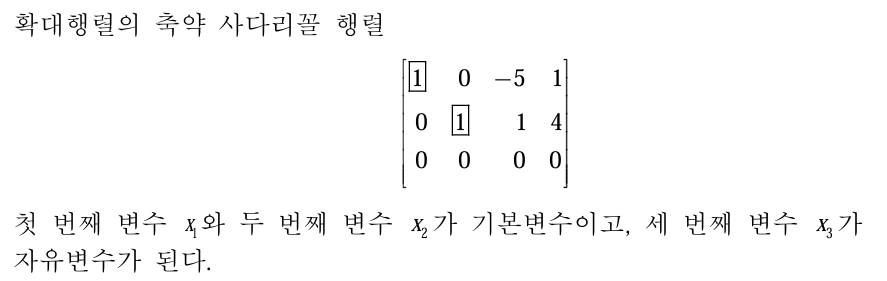

선형방정식에서 해 집합 표현을 매개변수 표현(Parametric Description) 방식으로 전개할 수 있다.


선형방정식을 풀 때는 다음과 같은 원칙을 적용하면 된다.
-
선형방정식을 확대행렬로 변형한다.
-
기본행 연산을 사용하여 사다리꼴 행렬로 만든다.
-
만약 해가 존재하지 않으면, 알고리즘을 중지한다. 그렇지 않고 해가 존재한다면 다음 단계를 진행한다.
-
사다리꼴 행렬에 기본행 연산을 계속 수행하여 축약 사다리꼴 형태로 만든다.
-
축약 사다리꼴 행렬을 변수를 포함한 선형 방정식으로 변환하고, 각 기본 변수를 자유 변수로 표시하여 일반해를 구한다.
