
1. 선형결합
선형결합(일차결합)은 벡터들을 어떤 스칼라(수)로 곱하고 더한 것을 말한다. 같은 차원이 여러 벡터들을 실수배하여 더한 식이다.

- 벡터(선형)방정식 : 선형방정식의 계수를 열벡터로 표현하고, 벡터
b를 선형결합으로 나타내는 것을 말한다.
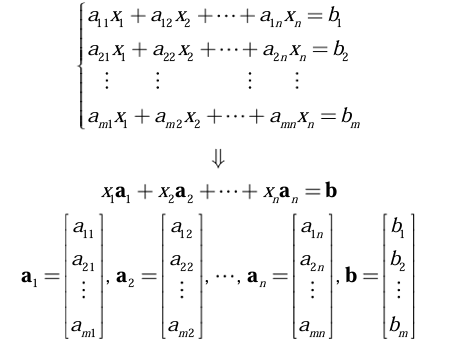
선형방정식의 해를 구한다는 것은 열벡터들로 벡터 b를 어떻게 선형결합으로 나타낼 수 있는가를 찾는 문제와 동일하다.

2. 선형결합의 Span 표현
Span은 벡터들이 만들어내는 모든 선형결합의 집합을 의미한다.


해 공간을 설명할 때 연립방정식들의 해가 어떤 Span에 있는 것인지 확인하는 것이 중요하다. 만약 해가 Span 범위 내에 없다면 해가 없는 것이다.
반대로 어떤 해가 Span 범위 내에 속한다는 것은 벡터 방정식이 해를 갖는다는 것과 동일하다.
3. 벡터 및 행렬 방정식의 해
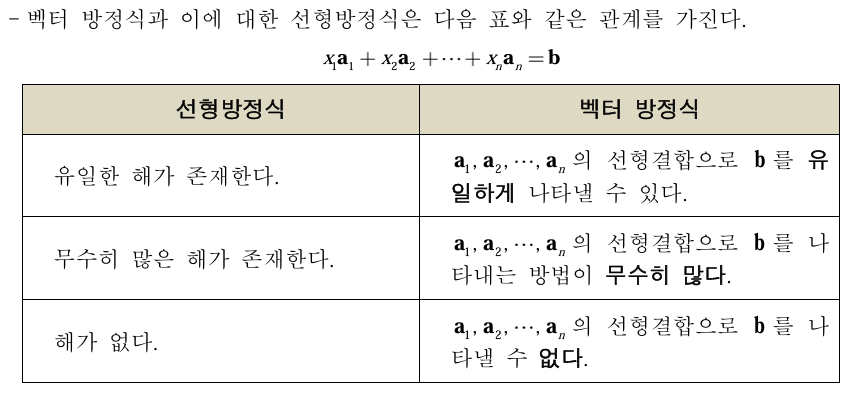
비동차선형방정식에서는 상수 b에 따라서 해의 위치가 달라진다. 그러나 해의 규모가 달라지는 것은 아니다.
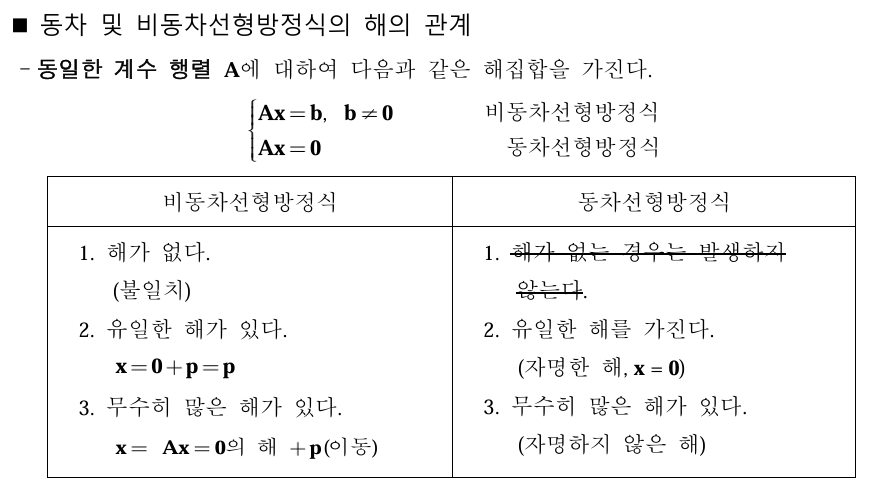
- 특이해(Partifular Solution) :
Ax = 0의 해를p만큼 위치 이동 시킬 때,p를 특이해라고 한다.
비동차방정식에서 특이해를 포함하면 전체 해집합은 원점을 지나지 않는다.

4. 독립과 종속
벡터의 집합 중 하나를 이용해서 나머지 벡터의 선형결합으로 나타낼 수 있다면 그것은 종속이다. 종속은 결국 어떤 것이 나머지로 만들어질 수 있는 즉, 겹치는 상태이다. 이와 달리 독립은 서로 겹치는 것이 없어 다른 방향으로 뻗어나가는 것이다.

어떤 벡터들의 선형 결합의 해가 모두 0이라면 서로 독립이자 일차독립(Linearly Independent)이다. 그러나 적어도 어느 하나가 0이 아닌 값을 가지면 서로 종속이자 일차종속(Linearly Dependent)이다.
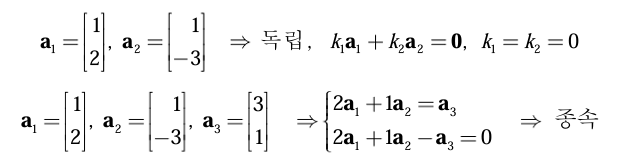
참고로 벡터가 n차원 공간을 Span하려면 n개의 선형독립벡터가 필요하다.
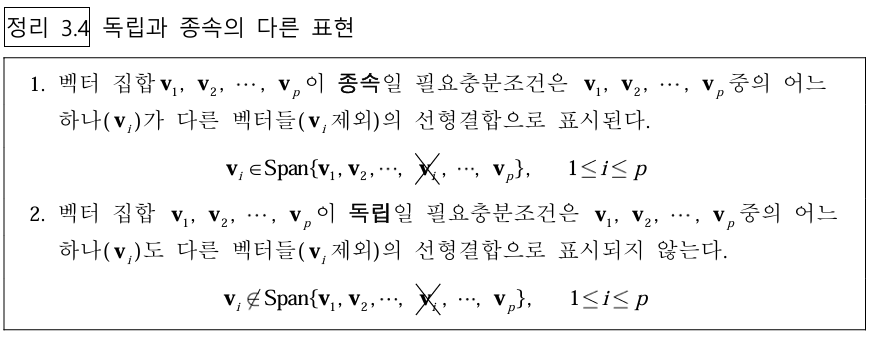
4-1. 독립의 필요 충분 조건

동차선형방정식이 자명한 해를 가지는 경우, 행렬 A의 모든 열에 피봇이 존재한다. 모든 열에 피봇이 존재하면 독립이 된다.
이와 반대로 자유 변수가 존재하면 무수히 많은 해가 존재하고, 많은 해들 중에서 적어도 하나는 0이 아니므로 종속이 된다.

1번의 경우, 영 벡터가 아닌 하나의 벡터는 독립인데, 이는 당연히 자기 1개뿐이라 독립이 될 수 밖에 없다. 4번의 경우, 예를 들어 3차원 공간에 벡터가 4개 존재하면 어떤 벡터가 나머지 셋의 조합이 될 수 밖에 없으므로 종속이 된다.
4-2. 독립 벡터 집합의 유일한 선형 결합
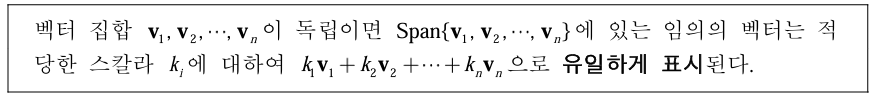
3차원의 표준 단위 벡터는 서로 독립이고, 3차원의 임의의 벡터 v는 두 벡터의 선형결합으로 유일하게 표현될 수 있다.
4-3. 독립과 관련된 정칙행렬의 성질

8번의 경우, 열 벡터들의 집합은 독립이라 서로 정보가 겹치치 않는다는 것을 의미한다. 9번의 경우, 최초 n개의 독립벡터들이 있어야 n차원의 선형결합으로 나타낼 수 있다는 것을 의미한다.
