[2025-1학기] 선형대수학 - 벡터의 외적

1. 벡터의 외적

벡터의 내적은 스칼라 값 1개가 나오지만, 벡터의 외적은 방향과 크기를 가진 또 다른 새로운 벡터를 만들어 낸다.

1-1. 외적의 성질

외적은 교환 법칙이 성립하지 않는다. u × v가 0이라면 u, v가 같은 방향이거나 평행한 경우이다. 외적 벡터가 존재하지 않는다.

외적과 내적에 대해서 다음과 같은 내용이 성립된다.

1-2. 오른나사 법칙

두 벡터의 외적은 두 벡터와 동시에 수직인 벡터이고, 그 방향은 오른손을 감아 쥐었을 때, 펼친 엄지 손가락 방향과 동일하다.

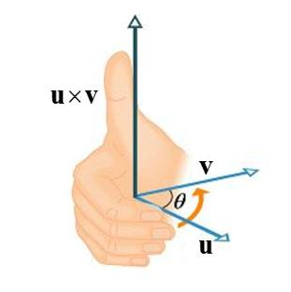
1-3. 외적의 크기

1-4. 스칼라 3중적

u, v, w를 3차원 공간 상의 세 벡터라고 할 때, 세 벡터 u, v, w의 스칼라 3중적은 u (v × w)으로 정의한다.

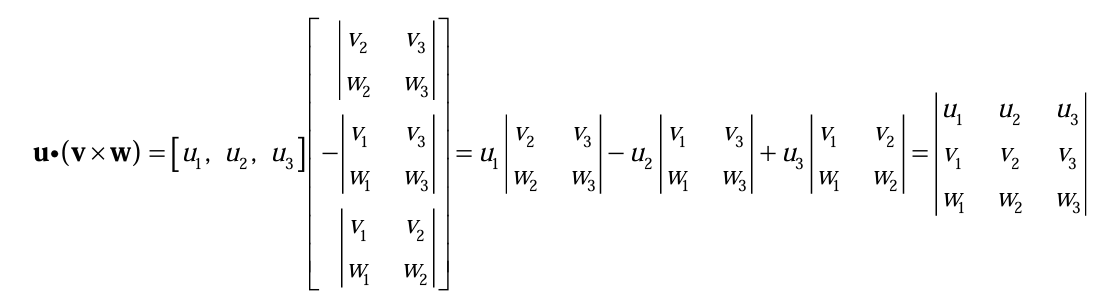
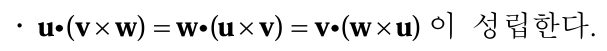
순서를 바꿔도 성립된다는 것을 잊지 말자.

1-5. 사면체의 부피

1-6. 동일한 평면 위

세 벡터가 같은 시점을 갖고, 동일한 평면에 있기 위한 필요 충분 조건은 다음과 같다.