
1. 벡터와 스칼라
-
벡터(Vector) : 속도, 자기장과 같이 크기와 방향을 갖는 물리적인 양(값)을 의미한다.
-
스칼라(Scalar) : 길이, 면적, 질량과 같이 크기만을 갖는 양(값)을 의미한다. 스칼라는 '실수'이다.
2. 벡터의 크기, 역벡터, 영벡터
-
단위 벡터(Unit Vector): 크기가 1인 벡터를 말한다.
-
역벡터 : 벡터
a에 대하여 크기가 같고 방향이 반대인 벡터를 말한다. 기호로는-a로 나타낸다. -
영벡터 : 시점과 종점이 일치하는 벡터를 말하며, 기호로는 0으로 나타낸다.
참고로, 벡터의 크기는 놈(Norm)이라고 하며, 벡터의 집합은 행렬이다.
또한, 시점의 위치에 관게 없이 두 벡터 a, b의 크기가 같고 방향이 일치할 때, 두 벡터는 같다고 말할 수 있다. a=b가 된다.
벡터는 크기와 방향이라는 2가지 성분이 존재하기 때문에 2차원 공간 이상에서 정의된다. 이에 반하여, 스칼라는 크기만으로 표시되므로 1차원 실수값으로 표현된다.
그렇다면 1차원 수직선에 벡터를 나타낼 수 있을까?
1차원에서는 동일한 방향을 갖고 있기 때문에 벡터를 나타낼 수 없다. 벡터는 2차원 공간에서부터 나타낼 수 있다. 2차원에서는 방향성이 존재하기 때문이다.
3. 벡터의 종류
-
위치 벡터 : 원점을 시점으로 하는 벡터를 말한다. 즉, O을 원점이라 할 때, 벡터 OA는 위치 벡터이다.
-
자유 벡터 : 시점이 원점이 아닌 벡터를 말한다. 자유 벡터는 항상 위치 벡터로 바꿀 수 있다.
시점과 종점이 있으면 벡터끼리 비교하기 어렵기 때문에, 두 벡터를 비교할 때에는 기준점을 맞추는 이동이 필요하다. 특히, 벡터의 평행 이동에 의해 동일한 벡터들을 하나로 표현할 수 있다.
각 차원에 따른 벡터 표현은 좌표, 행벡터, 열벡터로 표현 가능하다.

4. 벡터의 연산
벡터의 연산에는 덧셈과 실수배(스칼라배) 2가지가 있다.
4-1. 벡터의 덧셈
두 벡터 a, b에 대해서 AC로 나타내어지는 벡터 c를 벡터 a, b의 합이라고 하고 c = a + b 또는 AC = AB + BC로 나타낼 수 있다.
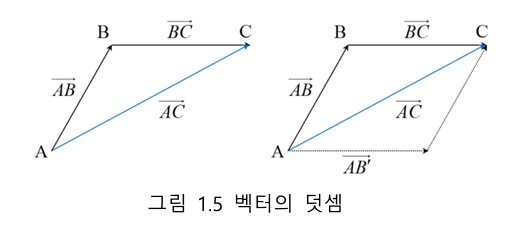
벡터의 뺄셈은 역벡터의 덧셈으로 정의할 수 있으며, 벡터의 덧셈 성질은 다음과 같다. 교환 법칙, 결합 법칙, 항등원, 역원 모두 성립한다.

4-2. 벡터의 실수배
벡터의 실수배 역시 다음과 같이 성립한다. 결합 법칙, 배분 법칙 모두 성립함을 알 수 있다.


5. 기억해야 할 부분
-
1차원 공간에서는 방향성이 없기 때문에, 벡터는 최소 1차원 공간 이상에서 정의할 수 있다.
-
벡터는 공간에서 점의 좌표로 표시할 수 있다.
-
벡터의 연산은 같은 차원에서 수행된다. 예를 들어, 2차원 벡터와 3차원 벡터를 덧셈하는 경우는 불가능하다.
-
벡터는 하나의 변수로 여러 성질을 표현할 수 있다. 즉, 관심 대상의 여러 성질을 한꺼번에 나타낼 수 있다는 점에서 벡터는 데이터의 묶음이다.
