[2025-1학기] 선형대수학 - 행렬의 정의와 연산

1. 행렬

• 행렬 : 수 또는 문자를 괄호 () 또는 [] 안에 직사각형의 모양으로 배열한 것을 말한다. 괄호 안의 수나 문자를 그 행렬의 성분 또는 원소라 한다.

행의 개수가 m개, 열의 개수가 n개인 행렬을 크기가 m × n 행렬 또는 m × n 차원 행렬이라고 한다.

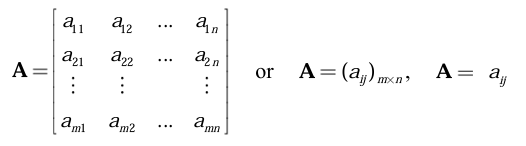
• 정방(정사각) 행렬(Square Matrix of Order n) : m = n인 행렬을 의미한다.

• 주대각성분(Main Diagonal) : 대각선에 위치한 성분들을 의미한다.

• 열 벡터(Column Vector) : 크기가 m × 1인 행렬을 의미한다.

• 행벡터(Row Vector) : 크기가 1 × n인 행렬을 의미한다.

이렇게 보면, 행렬은 열 벡터들의 집합 또는 행 벡터들의 집합으로 볼 수 있다.

1-1. 행렬의 덧셈 성질

같은 크기의 행렬일 때 다음과 같은 성질이 성립한다.

1-2. 행렬의 스칼라 곱셈 성질

A, B가 m × n 행렬이고, k, l이 임의의 스칼라일 때 다음과 같은 성질이 성립한다. 스칼라는 실수라고 생각하면 더 쉽다.

1-3. 행렬의 곱셈 성질

행렬의 곱셈을 수행할 때 연산을 주의해야 한다. 한 행의 원소와 한 열의 원소를 서로 곱하고 더해서 하나의 원소로 나타낸다.

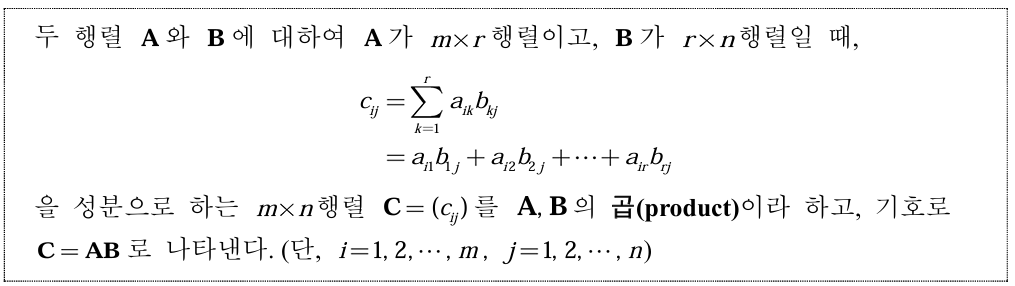
지금까지 연산해온 방식과 많이 달라서 궁금했었다. 행렬의 곱셈을 이렇게 복잡하게 하는 이유는 새로운 정보를 만들기 위해서이다.

그리고 행렬의 곱셈이 가능한 경우는 m × r 행렬과 r × n 행렬처럼 한 행렬의 행과 한 행렬의 열의 크기가 같아야 한다.

참고로 AB = BA가 아니라는 점을 잊지 말아야 한다. (교환 법칙 성립 X) 아래의 문제를 통해 AB와 BA가 다르다는 것을 알 수 있다.

5번을 가장 헷갈리기 쉬울 것 같다. 교환 법칙이 성립하지 않기 때문에, 우리가 기존에 알고 있는 교환 법칙 공식을 이용하면 안된다. (교환 법칙 : 어떤 것을 먼저 곱하든 곱의 결과는 변하지 않는다는 수학적 약속)

2. 역행렬

• 단위 행렬 : n차 정사각형 행렬 중에서 주 대각선의 원소가 I이고, 나머지 성분이 모두 0인 행렬을 n차 단위 행렬이라고 한다. 기호로 I를 사용해서 나타낸다.

단위 행렬은 행렬의 곱셈에 대한 항등원 역할을 하며, A · I = A = I · A이 성립한다.

• 역행렬(Inverse Matrix) : AB = I = BA를 만족하는 B가 존재할 때, A를 정칙행렬(Regular Matrix), 비특이행렬(Non-Singular Matrix), 가역 행렬(Invertible Matrix)라고 한다. B는 A의 역행렬이라고 하며, 기호로는 $A^{-1}$ 나타낸다.

A가 정칙행렬이 아니라면, A는 비정칙행렬(Irregular Matrix), 특이행렬(Singular Matrix), 비가역적(Not Invertible)이라고 한다. 정칙 행렬이 아니라면 역행렬이 될 수 없다는 것을 알 수 있다.

정칙행렬 A의 역행렬은 오직 하나 뿐이다. A가 정칙행렬이고 B, C가 A의 역행렬이면 B와 C는 동일하다.

2-1. 역행렬의 성질

$(ABC)^{-1}$의 경우에 2번을 적용하면 $C^{-1}B^{-1}A^{-1}$가 된다. 5번의 경우에는 역행렬을 n번 곱해도 값이 똑같다는 것을 의미한다.

다만 A, B가 정칙행렬일 때 A + B도 정칙행렬이지만, $(A + B)^{-1}$은 $A^{-1} + B^{-1}$이 될 수 없음을 기억해야 한다.

2-2. 비정칙행렬 및 정칙 행렬의 성질

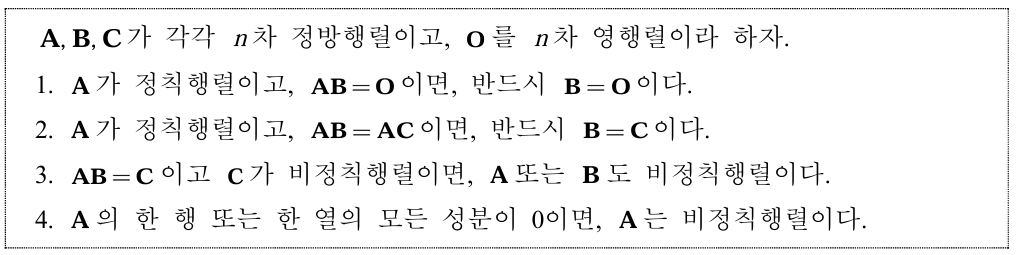
2번의 경우, A가 역행렬을 가졌다면 약분할 수 있다는 것을 의미한다. 4번의 경우에도 한 행 또는 한 열의 모든 성분이 0이면 차원이 축소되기 때문에 A가 비정칙행렬이 될 수 밖에 없다.