[2025-1학기] 선형대수학 - 여인수 행렬, 수반행렬, 행렬식 응용

동차선형방정식 Ax = b는 Det(A)이 0이 아닐 때, 자명한 해를 갖는다.

1. 여인수 행렬과 수반행렬

여인수들로 구성된 행렬을 여인수 행렬(Cofactor Matrix)라고 하며, 이 여인수 행렬의 전치행렬을 수반행렬(Adjoint Matrix of A)라고 한다. 기호로는 adj(A)로 나타낸다.

수반행렬은 꼭 여인수 행렬을 Transpose 해줘야 한다.

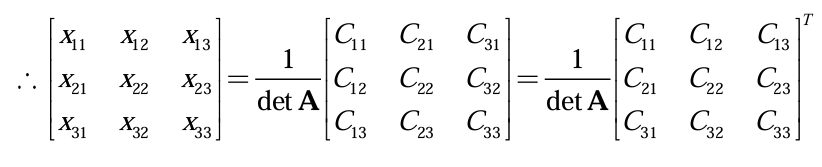
참고로 역행렬은 Det(A)가 절대 0이 될 수 없다. $A^{-1}$ = $1/Det(A)$ · $adj(A)$이기 때문이다.

기본행렬(가우스 소거법)을 이용하여 역행렬을 구하는 것은 역행렬 값만 구할 때 사용한다. 하지만 여인수 전개를 사용하여 역행렬을 구하는 것은 역행렬의 성질을 분석할 때 사용한다.

2. 수반행렬의 성질

수반행렬의 행렬식은 원래 주어진 행렬의 행렬식을 이용하여 구할 수 있다.

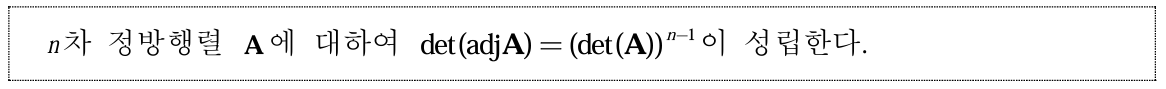
3. 행렬식의 응용

행렬식을 이용하면 넓이나 부피, 직선의 방정식, 타원의 방정식, 평면의 방정식을 쉽게 구할 수 있다.