
1. 선형방정식
선형방정식(Linear Equation)은 변수의 최고차 항의 지수가 1이다.

-
연립일차방정식(System of Linear Equation), 선형계(Linear System) : 동일한 변수에 대한 선형방정식의 유한개의 묶음을 말한다.
-
해 집합(Solution Set) : 모든 선형방정식의 해가 되는 집합을 의미한다.
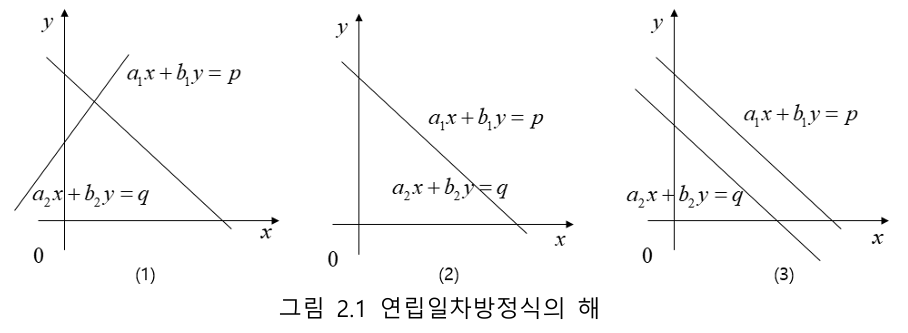
연립일차방정식의 해는 오직 하나(Unique)이거나, 무수히 많거나, 해가 없는 경우 중 하나이다. 연립일차방정식이 해를 갖지 않는다면 불일치(Inconsistent)라고 하고, 적어도 하나 이상의 해가 존재하는 경우를 일치(Consistent)라고 한다.
2. 선형방정식과 행렬
n개의 미지수와 m개의 방정식으로 이루어진 선형방정식을 행렬의 곱으로 간단하게 나타낼 수 있다.
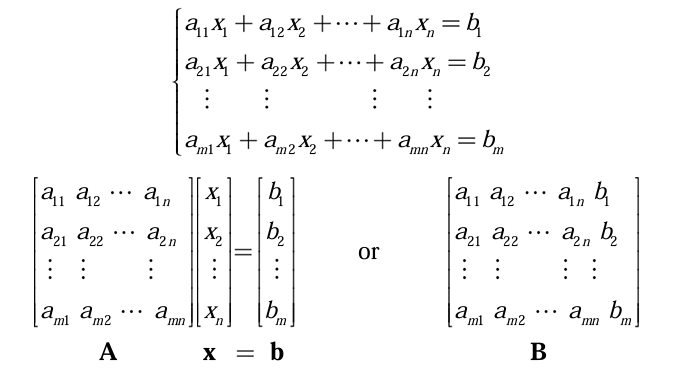
계수만 나타낸 행렬 A를 계수행렬(Coefficient Matrix)이라고 하고, 상수 b를 포함한 행렬 B를 확대행렬 또는 첨가행렬(Augmented Matrix)라고 한다.
2-1. 기본행 연산(Elementary Row Operation)
-
치환(Replacement) : 한 행에 0이 아닌 상수배를 한 뒤에 다른 행에 더한다. (가우스 소거법)
-
상수배(Scaling) : 한 행에 0이 아닌 상수배를 곱한다.
-
교환(Interchange) : 두 행을 교환한다.
참고로 ~ 기호는 기본행 연산을 수행하여 해 집합이 같다는 행동치를 의미한다.
기본행 연산은 역으로 초기 선형방정식으로 되돌릴 수 있다.
2-2. 해의 존재와 유일함의 문제
-
선형 방정식이 일치하다는 것은 그 해가 존재한다는 것을 의미한다. 해는 유일하게 하나만 존재하거나 또는 무수히 많은 해가 존재하는 경우가 있다.
-
해가 하나만 존재하는 선형방정식은 그 해가 유일한 해이다. 해가 두 개나 세 개가 존재하는 경우는 없다.
