
1. 기본 곱(Elementary Product)
각 행에서 원소를 하나씩 고르되, 열이 서로 겹치지 않게 고른다.

기본 곱에 부호를 붙이면 행렬식(Determinent)가 된다.
1-1. 전도 및 전도수
-
전도 : 어떤 큰 자연수가 작은 자연수보다 먼저 나타나 있을 때 전도되었다고 말한다.
-
전도수 : 하나의 순열에서 나타나는 전도의 총 개수를 전도수라고 한다. 결국 인덱스가 얼마나 엉켜있는지를 의미한다.
원래 1 → 2 → 3 순으로 가야하지만 3 → 2 → 1로 되어있는 경우, 전도 수는 3 → 2 (1회), 2 → 1 (1회), 3 → 1 (1회)로 하여 총 3회가 된다. 참고로 숫자는 2개씩 비교한다.
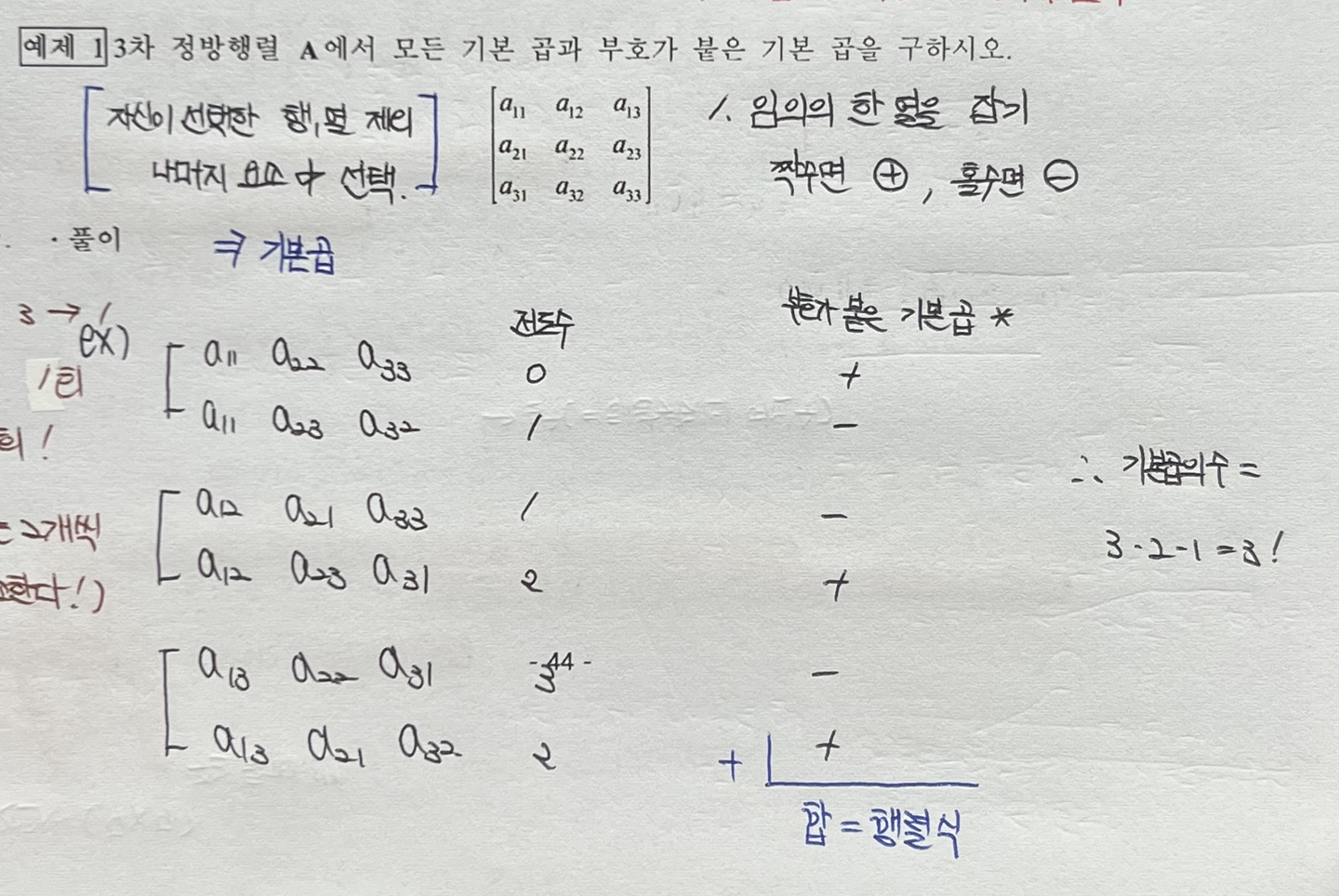
2. 행렬식
n차 정방행렬 A에 대해 부호가 붙은 모든 기본 곱들의 합을 A의 행렬식(Determinent of A)라고 한다. 행렬식은 실수 값이므로, 실수로 대응시키는 함수와 동일하다.

행렬식은 행 또는 열 벡터의 종속(평행, 겹침) 또는 독립을 판단한다. Det(A)의 값이 0이면 벡터들이 종속이고, 0이 아닌 경우에는 벡터들이 독립한다.
참고로 선형독립일 수록 더 많은 공간을 표현할 수 있다. 이는 다른 방향으로 많이 뻗어 있기 때문이다.
2-1. 소행렬과 여인수
- 소행렬(Minor) : 행렬에서
i행j열을 제거한 부분 행렬을 말한다.

- 여인수(Cofactor) : 소행렬의 행렬식에 부호를 붙인 값이다.
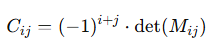
여인수의 부호는 i와 j의 합이 짝수이면 +이고, 홀수이면 -이다.


2-2. 여인수 전개
n차 정방행렬 A에 대한 행렬식 Det(A)는 임의의 i번째 행에 대한 여인수 전개, 또는 임의의 j번째 열에 대한 여인수 전개와 같다.
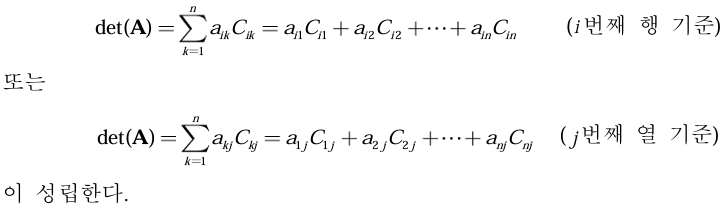
Laplace 소행렬식 전개라고도 하며, 행렬식은 재귀적인 정의 및 계산이라 볼 수 있다.
0이 많은 열 또는 행을 선택하면 행렬식을 더 쉽게 구할 수 있다.
2-3. Sarrus 법칙
행렬 A가 2차 또는 3차 정방행렬일 경우, Sarrus 법칙을 적용하여 행렬식을 구할 수 있다.
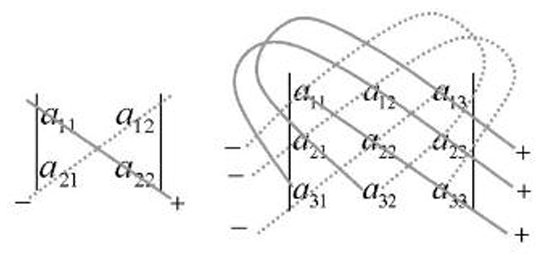
이 경우에 식으로 정리하면 Det(A) = (aej + bfg + cdh) - (gec + hfa + idb)로 나타낼 수 있다.

3. 행렬식의 성질
행렬 A가 삼각행렬 또는 대각행렬이면 A의 행렬식은 주 대각선성분들의 곱과 같다.

n차 정방행렬 A와 B에 대해서는 다음과 같은 성질이 성립한다.
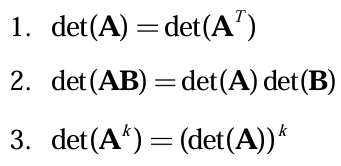
행에 대한 행렬식은 열에 대한 행렬식의 성질로 바꾸어도 항상 성립한다. 그리고 Det(A + B)은 Det(A) + Det(B)가 절대 될 수 없다.
정칙행렬에 대해서는 다음과 같은 성질이 성립한다.

기본행 연산에 대해서도 다음과 같은 성질이 성립한다.

가급적이면 행렬식을 구성하는 성분에 0이 많이 나올 수 있도록 치환한다. 주의할 점은 행렬식 계산에 적절한 것은 가우스 소거법(축약 사다리꼴)까지만 적용하는 것이다. 기약 사다리꼴은 여러 행 연산을 통해 1과 0 위주로 정리된 형태라 행렬식의 값이 바뀔 수 있기 때문이다.
행렬의 상수배에 대해서는 다음과 같은 성질이 성립한다.

4. 크래머 법칙
n × n 행렬이고 b가 n차원 벡터인 Ax = b의 선형방정식의 유일한 해를 구하는 데 적용하는 법칙이다. 해를 구하는 것보다 해의 수학적 성질을 조사하는 목적에 있다.

i번째 열 벡터 대신 b라는 열 벡터를 대입한다.


