이글은 공돌이의 수학정리노트 (출처: https://angeloyeo.github.io/2020/09/07/basic_vector_operation.html#%EA%B0%80%EC%9E%A5-%EA%B8%B0%EC%B4%88%EC%A0%81%EC%9D%B8-%EB%8D%B0%EC%9D%B4%ED%84%B0-%EB%B3%80%ED%98%95-%EB%B0%A9%EB%B2%95) 와 Michigan 대학교 Computational Linear Algebra (출처: https://github.com/michiganrobotics/rob101) 를 참고하여 만들었습니다.

0. Systems of Linear Equations 표현

우리는 이제 연립일차 방정식을 행렬과 벡터로 표현할 것이라고 배웠다. 그러면 어떻게 표현할까? 그건 매우 간단하다.

다음 연립 일차 방정식이 있다고 생각하자.

보통 연립 일차 방정식을 행렬,벡터로 표현할 때
로 정의한다.
(A는 변수(x,y,z같은)들의 coefficient를 담은 행렬 X는 변수들을 담은 열벡터 b는 상수항을 담은 열벡터)

위 예시를 예를 들면 다음과 같이 표현할 수 있다.

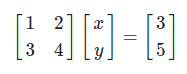
이제 연립 일차방정식을 행렬,벡터로 표현하는 가장 기초적인 방법을 배웠다. 이제 여러가지를 공부하며 이러한 연립 일차 방정식의 해집합을 구하는 방법에 대해서 우리는 공부할 것이다.

1. Vector

정의

벡터는 화살표다.

여기서 Vector는 우리가 일반물리에서 배운 Vector의 의미로 생각하면 된다. 즉,"크기와 방향을 정의하는 값"이다.(그냥 크기는 Scalar)

벡터는 숫자를 나열한 무언가다.

벡터에 대해 생각해볼 수 있는 정의는 "숫자를 나열한 리스트라는 관점"이다.

벡터를 그저 물리에서 배운 화살표라고만 생각하면 3차원까지 (3개의 숫자가 나열된 리스트)라고만 생각할 수 있지만 숫자를 나열한 리스트라고 생각한다면 차원을 무한히 확장할 수 있다.
(그냥 숫자나열만 디따 많으면 고차원이다. 인공지능에서 고차원이라는 말은 그냥 길게 나열한 숫자 리스트다)

Vector는 열벡터(Column Vector)

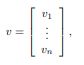
행벡터(Row Vector) 두가지 방식으로 정의할 수 있다

벡터란 벡터 공간의 원소

벡터를 엄밀한 수학에서 정의하는 방식이다. 수학에서 대수를 공부한다는 것은 공간을 정의한 다음 그 공간의 성질을 파악하는 것이다. 공간에 속하는 모든 원소는 그 공간의 성질을 따른다.

벡터 역시도 벡터 공간의 성질을 따르고 이런 유용한 성질을 가지고 우리는 연립 일차 방정식(Systems of Linear Equations)의 해집합을 구할 수 있다.

벡터 공간은 다음과 같은 세 가지 요소가 정의되고 성립되어야 한다.

$(V,+,\cdot)$
여기서 $V$는 벡터 $+$는 덧셈 규칙, $\cdot$은 곱셈 규칙을 의미한다.

Vector의 기본 연산

벡터의 기본 연산은 상수배,벡터 간의 합이다. 이것들은 우리가 일반물리에서 배운 개념들이다. (직관적으로 이해할 수 있다.)

Vector의 상수배 (scalar multipliation)

Vector의 상수배를 벡터공간으로 정의하면
임의의 집합 V에 대해 임의의 벡터 $x \in V$와 스칼라 $k \in R$ 에 대하여 다음이 성립하여야 한다.

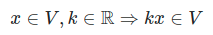
(.... 그냥 쉽게 이해해보자)

화살표를 통해 직관적으로 이해하면 화살표를 늘리거나 줄이는 과정이다.

Vector간의 합

Vector간의 합을 벡터공간으로 정의하면
임의의 집합 V에 대해 임의의 벡터 $x,y \in V$에 대하여 다음이 성립한다.

직관적으로 이해하면 아래 사진과 같다.

Vector 간의 선형 결합

Vector의 기본 연산을 배운 이유는 Vector 간의 선형 결합(Linear Combination)을 표현하기 위해서다.Vector의 상수배를 벡터공간으로 정의하면 다음이 성립한다.

말이 어렵지 그냥 Vector의 상수배와 벡터간의 합을 한번에 표현한것을 말한다.

Linear Combination이 중요한 이유는 공간(Subspace)을 만들기 때문이고 우리는 이 아이디어를 이용해 연립일차 방정식의 해집합을 해석할 것이다.

2. Matrix Multiplication 이해

우리는 단순히 행렬 곱셈의 공식만 암기하는 것이 아니라 그것이 무엇을 의미하는지 Insight을 얻는데 집중할 것이다.

일반적 행렬곱

행렬의 곱셈 방식은 좀 독특하다.

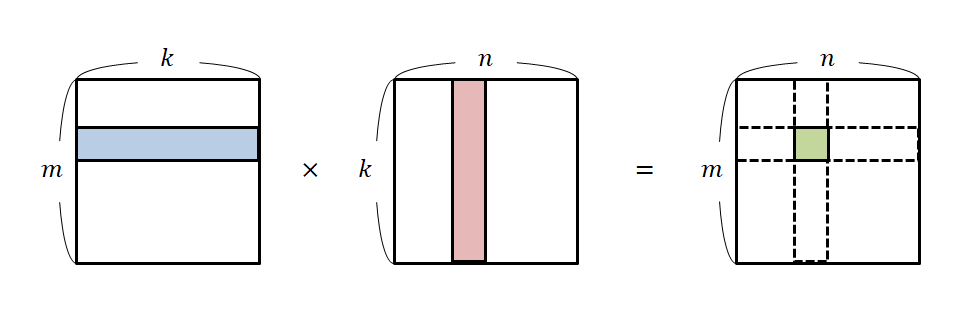
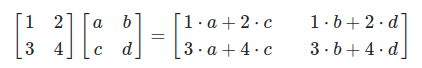
행렬곱의 이런 형태는 "행렬은 vector을 mapping하는 일종의 함수이고 행렬곱은 두 함수의 합성함수" 라는 아이디어를 받아들이면 된다.

행렬을 어떤 함수 $f,g: \mathbb{R}^2 \rightarrow \mathbb{R}^2$ 라고 생각해보자.

이 함수는 2차원의 벡터를 받아 2차원의 벡터로 mapping하는 함수이다.

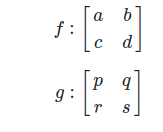
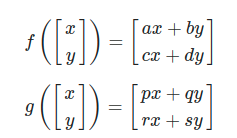
이때 두 함수 f,g의 합성함수는 다음과 같다.

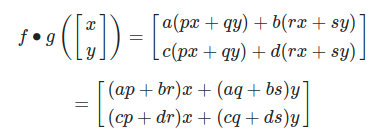
행렬의 곱은 함수의 합성함수이므로 행렬의 곱은 다음과 같이 표현할 수 있다.

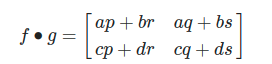
이제 왜 행렬의 곱이 이렇게 정의되었는지 알 수 있다.

하지만 중요한 건 저 공식 형태가 아니다.(저건 그냥 의미 몰라도 외우면 된다!!!
) 더 중요한 건 저 식으로부터 얻어야 하는
insight이다. 두 행렬의 곱 행태를 다시 관찰해보자.

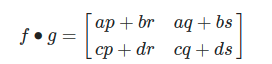
위 식으로부터 아래식을 보고 유추할 수 있는 것은

행렬곱의 각 원소값은 f의 열벡터와 g의 행벡터 각각의 내적을 표현하고 있다

즉, 일반적으로 이용하는 행렬곱의 관점은 행벡터와 열벡터같의 내적(inner product)을 계산함으로써 행렬곱이 이루어진다는 것을 알 수 있다. 이러한 행렬곱의 해석은 공분산을 구할 때 사용된다.

행렬곱은 열벡터의 선형결합

이번에는 행렬과 벡터의 곱에 대해 생각해보자.

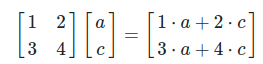
우리는 이 결과를 다르게 표현할 수도 있다.

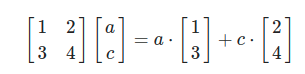
아까 우리는 벡터의 상수배와 벡터간의 합을 선형결합이라고 배웠다. 위 식은 행렬의 열벡터의 선형결합을 나타낸다. 즉 행렬의 곱을 열벡터의 선형결합으로 이해할 수 있다.

그러면 왜 이러한 해석이 중요할까? 아까 우리는 벡터 선형결합의 의미하는 것은 벡터 공간의 생성이라는 것을 배웠다. 행렬과 벡터의 곱이라는 수식이 우리에게 주는 깨달음은 주어진 열벡터들을 이용해 만들 수 있는 벡터공간(열공간,Column Space)이다.(행렬과 행렬의 곱은 행벡터와 열벡터의 내적)

처음 Systems of Linear Equation 수식을 예시로 들어보자.

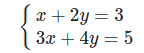
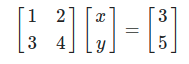
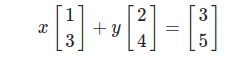
이 식이 우리에게 묻는 것을 위 열공간을 기반으로 번역하면

두 벡터 $[1 \quad 3]^T$ 와 $[2 \quad 4]^T$ 로 생성된 벡터공간 내에 벡터 $[3 \quad 5]$가 존재하는가? 이다.

어렵네 좀더 쉽게 풀어 써보자

두 벡터 $[1 \quad 3]^T$ 와 $[2 \quad 4]^T$ 의 조합으로 $[3 \quad 5]^T$가 만들어질 수 있는가?

이러한 관점으로 선형연립방정식의 해집합을 구한다 (우리가 원하는 연립방정식의 해를 구하는 Insight가 바로 이것이다.)

3.행렬과 선형변환

선형변환

임의의 벡터 $a,b$와 스칼라 $c$에 대하여 변환 T가 다음의 두 조건을 만족한다면 이 변환 T는 선형변환이다.

행렬은 위 조건을 만족하기 때문에 행렬은 선형변환이다.
선형 변환에는 대표적으로 shearing,rotation,permutation,projection등이 있다.

기하학적 관점

위 식을 통해 선형변환(=행렬곱은) 다음과 같은 성질을 만족해야 한다.
1. 원점의 위치는 변하지 않아야 한다.
2. 변환 후에도 격자들의 형태가 직선의 형태를 유지해야하낟.
3. 격자 간의 간격이 균등해야 한다.

위 세 조건을 모두 만족시키지 못하는 변환은 선형변환이 아니다.