대칭행렬

행렬 $A$가 그것의 전치 $A^\top$와 같으면 대칭행렬이라 부릅니다.

전치(Transpose)

아래, gif 출처는 위키피디아입니다.

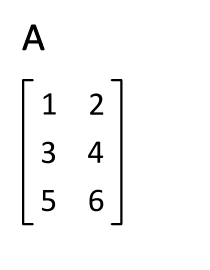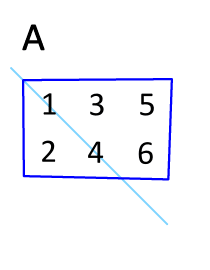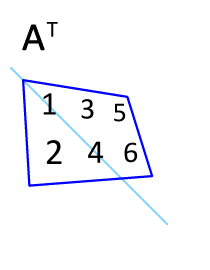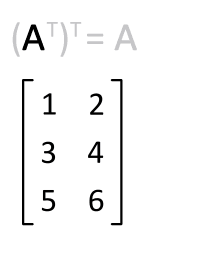
$A^\top$은, 행렬 $A$의 주대각선을 기준으로 반사하여 얻은 행렬입니다.

직교

대칭행렬과 직교는 매우 관련이 깊은 개념입니다.

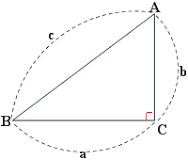
피타고라스 정리

우리 모두가 잘 알고 있는 피타고라스 정리는 직각삼각형에서 다음과 같은 관계를 설명합니다.
$c^2 = a^2 + b^2$
여기서 $c$는 빗변의 길이이고, $a$와 $b$는 다른 두 변의 길이입니다.

유클리드 거리

피타고라스의 정리를 2차원 평면에서 두 점 사이의 거리를 찾는 문제로 확장할 수 있습니다.

두 점 $P(x_1, y_1)$와 $Q(x_2, y_2)$ 사이의 거리 $d$는 다음과 같이 계산됩니다:
$d= \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$

이 공식은 2차원에서의 피타고라스의 정리의 확장으로 볼 수 있습니다. $x_2 - x_1$는 수평 변의 길이, $y_2 - y_1$는 수직 변의 길이를 나타내며, $d$는 두 점을 잇는 빗변의 길이, 즉 거리를 나타냅니다.

이러한 거리의 개념을 3차원, 4차원, 그 이상의 고차원으로 확장할 수 있습니다. 예를 들어, 3차원 공간에서 두 점 $P(x_1, y_1, z_1)$와 $Q(x_2, y_2, z_2)$ 사이의 거리는:
$d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2}$

이렇게 유클리드 공간에서의 거리는 차원이 높아져도 피타고라스의 정리를 기반으로 계속 확장됩니다.

유클리드 Norm (L2 Norm)

노름(또는 Norm)은 벡터의 "길이"나 "크기"를 측정하는 함수입니다. 유클리드 노름은 우리가 일반적으로 생각하는 거리 개념과 동일합니다.

벡터 $\mathbf{v} = [v_1, v_2, ..., v_n]$의 유클리드 노름은 다음과 같이 정의됩니다:

$||\mathbf{v}||_2 = \sqrt{v_1^2 + v_2^2 + ... + v_n^2}$

이 공식은 피타고라스의 정리를 일반화한 것입니다. 예를 들어, 2차원 벡터 $[v_1, v_2]$의 유클리드 노름은:

$||\mathbf{v}||_2 = \sqrt{v_1^2 + v_2^2}$

직교의 정의

두 벡터 $\bold a$와 $\bold b$의 내적이 0이라면, 두 벡터는 직교한다고 정의합니다.

직각

우리가 종이에 그린 "+" 기호를 생각하면, 그 두 선분은 직각을 이루고 있습니다.

직교

두 벡터가 "직교"한다는 것은, 그 두 벡터를 방향으로 원점을 지나는 선분을 그리면 원점에서 직각을 이루고 있다는 것을 의미합니다. 다시 말해, 두 벡터가 서로 수직이라는 것입니다.

좌표 평면 위에서 표준기저벡터 $\bold e_1,\bold e_2$를 그려보면, 그 벡터들이 "+" 기호와 같이 서로 만나며, 그 두 벡터는 서로 직교하고 있다고 말할 수 있습니다.

기하학적 직관

두 직선이 교차하여 인접한 두 개의 같은 크기의 각을 형성하면, 그 두 직선은 서로 수직하다고 볼 수 있습니다. 이것은 일반적인 직각의 개념으로, 두 직선이 90도의 각으로 만나게 됩니다.

이런 직감은 기하학을 처음 배울 때부터 익숙해지게 되며, 수학적 표현이나 정의를 알기 전에도 대부분의 사람들은 두 선이 서로 어떻게 수직으로 보이는지에 대한 기본적인 직감을 가지고 있습니다.

유클리드 원론으로부터의 설명

이 접근법은 고대 그리스 수학자 유클리드가 그의 저서 "원론"에서 사용한 방식을 따릅니다. 이 방법은 선험적 직관에 기반하여 기하학적 개념을 구축합니다.

1. 누구나 직각이 무엇인지 압니다: 이것은 기본적인 직감에 기반한 것입니다. 누구나 보고 '이것은 직각이다'라고 말할 수 있는 그런 각을 말합니다.
2. 직각 삼각형의 정의: 한 각이 직각인 삼각형을 정의합니다.
3. 피타고라스 정리의 증명: 주어진 직각삼각형에서 빗변의 제곱이 다른 두 변의 제곱의 합과 같다는 것을 증명합니다.

내적공간을 이용한 접근

0. 내적 공간:

내적은 주어진 벡터 공간에서 두 벡터를 받아 스칼라 값을 반환하는 연산입니다. 기본적인 내적의 성질들이 있으며, 이 연산은 벡터 간의 어떤 "상호 작용" 또는 "근접성"을 측정하는 데 사용될 수 있습니다.

일반적인 유클리드 내적(dot product) 외에도 다양한 내적 연산이 있을 수 있으며, 그 정의는 주어진 벡터 공간과 연구 대상에 따라 다를 수 있습니다.

다만, 모든 내적은 다음의 성질들을 만족해야 합니다: (스칼라 field =$\mathbb{R}$인 경우)
1. $\mathbf{a}$이 $\bold 0$이 아니면, $\langle \mathbf{a}, \mathbf{a} \rangle > 0$ (양의 정부호)
2. $\langle \mathbf{a}, \mathbf{b} \rangle = \langle \mathbf{b}, \mathbf{a} \rangle$ (대칭성)
3. $\langle c\mathbf{a} + \mathbf{b}, \mathbf{d} \rangle = c \langle \mathbf{a}, \mathbf{d} \rangle + \langle \mathbf{b}, \mathbf{d} \rangle$ (선형성)

1. 내적을 통한 직각의 정의:

두 벡터의 내적이 0이라면, 그 두 벡터는 "직교"한다고 정의합니다. 이 정의는 내적의 성질에 근거하여, 두 벡터가 어떤 의미에서 "상호 독립" 또는 "수직"임을 나타냅니다. 이것은 기하학적 직감을 수학적으로 표현한 것입니다.

$\langle \mathbf{a}, \mathbf{b} \rangle = 0$
이 조건은 두 벡터 $\mathbf{a}$와 $\mathbf{b}$가 직교한다는 것을 의미합니다.

2. 거리의 정의 (피타고라스의 정리의 확장):

내적을 기반으로 한 노름(nNorm)을 정의할 수 있습니다. 특히 유클리드 내적에서는 노름이 벡터의 길이로 해석됩니다. 피타고라스의 정리가 성립하도록 벡터의 길이$\bold v$를 수학적으로 정의할 수 있습니다.
$\|\mathbf{v}\|=\sqrt{\langle \mathbf{v}, \mathbf{v} \rangle}$

유클리드 내적

우리에게 가장 익숙한, 직교의 개념을 포장하러 가봅시다.

유클리드 내적은 우리가 일상적으로 사용하는 유클리드 공간에서의 내적을 의미합니다. 이 내적은 우리가 흔히 아는 직교, 거리, 각도와 같은 기하학적 개념들의 근간을 이룹니다.

정의

두 벡터 $\mathbf{a} = (a_1, a_2, \dots, a_n)$와 $\mathbf{b} = (b_1, b_2, \dots, b_n)$에 대한 유클리드 내적은 다음과 같이 정의됩니다:

$\langle \mathbf{a}, \mathbf{b} \rangle = a_1b_1 + a_2b_2 + \dots + a_nb_n$

기하학적 의미

1. 길이 (또는 노름)의 계산:
   벡터 $\mathbf{a}$의 길이(또는 노름)는 유클리드 내적을 이용하여 계산됩니다:

   $||\mathbf{a}|| = \sqrt{\langle \mathbf{a}, \mathbf{a} \rangle} = \sqrt{a_1^2 + a_2^2 + \dots + a_n^2}$

2. 직교:
   두 벡터가 직교한다는 것은 그 두 벡터의 유클리드 내적이 0이라는 것을 의미합니다. 즉, 두 벡터 $\mathbf{a}$와 $\mathbf{b}$가 직교하는 것과 다음이 같은 말입니다.

   $\langle \mathbf{a}, \mathbf{b} \rangle = 0$

3. 각도:
   두 벡터 사이의 각도는 내적을 통해 다음과 같이 계산됩니다:

   $\cos(\theta) = \frac{\langle \mathbf{a}, \mathbf{b} \rangle}{||\mathbf{a}|| \cdot ||\mathbf{b}||}$

   여기서 $\theta$는 두 벡터 사이의 각도입니다.