들어가며
스펙트럴 정리의 이해와 그 증명 방법들
다양한 방법으로 스펙트럴 정리를 접근할 수 있습니다. 각 방법은 그만의 장단점을 가지고 있으며, 개인의 수학적 배경과 관심사에 따라 가장 적합한 방법을 선택하는 것이 좋습니다. 저는 (증명을 직관적으로 이해하는 것보다) 증명 안에 들어 있는 (다른 정리 증명에도 통하는) 통찰을 읽기 위해서, 노력하는 과정이 더 재밌습니다. 그러므로, 다음과 같은 방식으로 접근하려 합니다.
스펙트럴 정리는 대칭행렬에 대한 중요한 성질을 다룹니다. 특히 실수 성분의 대칭행렬은 항상 직교 기저대각화를 할 수 있다는 사실을 주장합니다. 이러한 성질을 이해하고 받아들이기 위한 다양한 접근법이 있으며, 그 중 우리가 살펴볼 방법을 단계별로 요약하면 다음과 같습니다.
- 쌍선형형식과 dual space의 탐구
- 쌍선형형식과 dual space의 성질을 깊게 탐구하며, 이를 통해 스펙트럴 정리의 본질을 이해합니다.
- 장점: 수학적 기초가 상대적으로 덜 필요하다. (쉽단 뜻이 아니라 해석학 베이스가 없단 뜻입니다.) 모든 종류의 스펙트럴 정리를 이해하기 필요한 대수학적 기초를 제공해준다.
- 단점:
이런 식으로 설명하면, 듣는 사람이 괴롭다가장 큰 문제는, (해석학을 전혀 안쓰면 구체적인 스펙트럴 정리는 증명 안됩니다.) 구체적으로 실수성분대칭행렬이 직교 대각화가 된다는 결론이 아닌 (더 약한) 결론에 도달한다는 것이다. 더 구체적으로 말해서, 만약 실수성분의 대칭행렬이 고유벡터를 가지면, 직교대각화가 가능하다는 것만 알게 되는 것이다.
1단계가 끝나면, 실수성분의 대칭행렬의 특성다항식이 실근을 가지는 것을 보이는 문제만이 남습니다. (실수성분의 대칭행렬의 특성다항식이 실근을 가지는 것을 보이면, 대칭행렬이 (실수체 위의 벡터공간에서) 고유벡터를 가진다는 결론에 도달합니다.) 이 작업을 위한, 2가지 길이 있어요.
2-1. 대수학의 기본 정리 활용
대수학의 기본 정리는 해석학적 내용입니다. 제가 아는 바로는, 순수 대수학적 증명은 없습니다.
- 장점: 직관적이며 이해하기 쉽다. 서로 다른 수학 분야 간의 연결점을 보여준다.
2-2. 컴팩트 집합 위의 연속함수 활용
- 연속함수가 컴팩트 집합 위에서 최대값을 가진다는 성질을 활용하여 스펙트럴 정리를 설명합니다.
- 장점: 수학의 기본적인 내용으로 구성되어 있다. 대수학의 기본 정리를 전제하지 않으면서, 실수성분대칭행렬이 직교 대각화가 된다는 결론에 도달한다. (대수학의 기본정리를 컴팩트 집합 위의 연속함수의 성질로 증명가능하다는 것을 고려하면 이런 증명이 가능함이 이상하지 않습니다.)
- 단점: 대수학의 기본 정리 직접 활용하는 방법에 비해서 비전공자 대상으로의 설명력이 떨어진다. ( 대수학의 기본정리 증명을 엄밀하게 하고 대수학의 기본 정리 활용하는 것보다는 훨씬 쉽습니다. 그러나, 대수학의 기본정리는 그 내용이 많이 친숙해요. 증명없이 믿게 만들기도 쉽구요. 다시 말해서, 엄밀성만 포기하면 직관적인 설명의 설명력이 엄청나요. 근데, 컴팩트 집합같은 것은 수학과학생아니면 별로 안 친숙해요.)
우리는 위에서 소개한 과정을 모두를 할 것입니다. 먼저, 내용전개에 필요한 용어부터 정의하고 엄밀하게 증명하는 식으로 내용이 전개 됩니다.
여기서 부터의 포스팅은 스펙트럴 정리(특히 실수체위에서)의 증명을 기술이 목적이기 때문에, 증명이 완료되기 전까지는 내용이 어떤의미를 가지는지 또는 예시가 무엇이 있는지 굳이 적지 않을 겁니다. 그리고, 체의 정의 벡터공간의 정의 이런 것들 (적기 따분한것들)은 적지 않습니다. (지면이 부족해요. 블로그는 책이 아니니까요.)
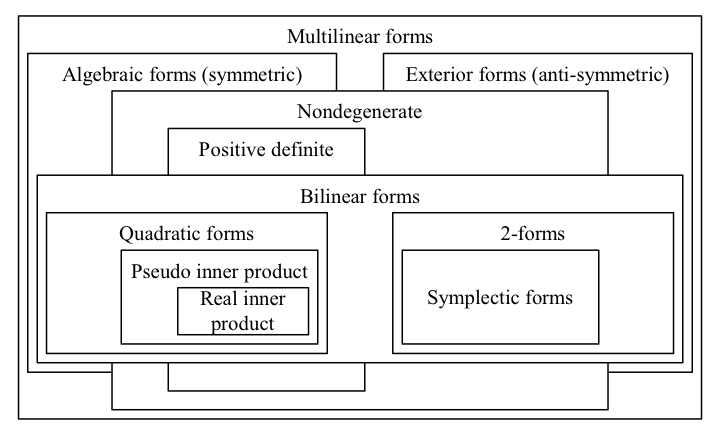
썸네일 해설:
- 모든 겹치지 않는 사각형들은 독립적(서로소)입니다.
- 사각형 간의 포함관계는 해당하는 개념 간의 포함관계를 반영합니다.
- 이 그림은 Field characteristic이 2가 아닐 때만 유효합니다. (char=2에서는 대칭과 반대칭을 구분할 수 없습니다.)
대칭행렬 소개:
대칭행렬은 대칭 쌍선형함수의 행렬 표현입니다. 이를 통해 다음의 주요 사실들을 관찰할 수 있습니다:
- 벡터공간 와 스칼라 field 에 대해, 는 다음을 만족할 때 대칭쌍선형함수입니다:
- 정방 행렬 가 모든 열벡터 에 대하여 를 만족하면, 는 대칭행렬입니다.
행렬과 선형변환의 관계:
우리가 행렬을 이용하여 선형시스템을 해결할 때, 그것은 사실상 선형변환의 문제를 해결하는 것과 같습니다. 마찬가지로 대칭행렬 문제 역시 선형대수학적 관점에서 바라보면 쌍선형형식의 문제로 해석됩니다.
그러나, 당장 이 관계를 정확하게 이해하는 것은 쉽지 않습니다. 왜냐하면, 행렬 전치가 추상적 관점에서 해석되지 않았으니깐요. 예컨데, 행렬의 곱은 선형변환의 합성으로 해석되는데, 행렬의 전치(또는 열벡터의 전치)는 선형변환의 무엇에 해당하는지를 이야기하지 않았습니다.
다음 두 문장을 보시면, 제가 무슨 말을 하고싶은지 이해되리라 생각이 듭니다.
- 참인 문장: 임의의 선형함수 에 대하여, 과 와 동치입니다. 여기서 는 의 기저입니다.
- 틀린 문장: 모든 의 기저 에 대해, 어떤 선형함수 가 모든 에 대해 를 만족합니다.
이차형식 (Quadratic Form)
이차형식은 개의 변수로 이루어진 2차방정식을 의미합니다.
여기서, 는 상수이며, 각 는 변수를 나타냅니다.
행렬로의 표현
위의 이차방정식은 행렬의 형태로도 나타낼 수 있습니다. 이를 표현하기 위해서는 대칭행렬가 필요하며, 이차형식은 다음과 같이 나타낼 수 있습니다:
여기서, 는 대칭행렬이며, 는 열 벡터입니다. 이 표현은 개의 변수를 가진 이차형식이 어떻게 행렬과 벡터의 곱으로 나타낼 수 있는지를 보여줍니다.
이유
이차형식을 대칭행렬로 표현할 수 있다는 것은 직관적이지 않을 수 있습니다. 그 이유는 이차형식의 각 항들이 의 형태로 주어지기 때문입니다. 곱셈의 교환법칙에 따라 임을 고려하면, 이차형식의 계수들을 조절하여 대칭행렬로 표현할 수 있음을 확인할 수 있습니다. 구체적으로, 만약 일반적으로 라면, 이를 평균화하여 대칭행렬의 형태로 변환할 수 있습니다. 즉, 새로운 계수 와 를 다음과 같이 정의합니다:
그러면 새롭게 구성된 (로 구성되는) 행렬은 대칭행렬입니다.
그러면, 이므로, 를 성분으로 하는 행렬 (즉, 대칭행렬)을 이용해서 이차형식을 기술 할 수 있습니다.
이 때, 스칼라 field의 charicteristic이 2가 아님을 전제로 합니다(char ), 그래야만 2의 (곱의) 역원이 존재하며 위의 평균화가 가능합니다.
이처럼, 이차형식을 대칭행렬로 표현하는 것은 스칼라 필드의 특성과 곱셈의 교환법칙에 기반합니다.
또한, 만약 서로 다른 두 대칭행렬이 에 대해서, 이차형식 가 각각 주어지면, 그들은 다릅니다. (다시말해서, 어떤 열벡터 가 존재해서 를 만족합니다.
