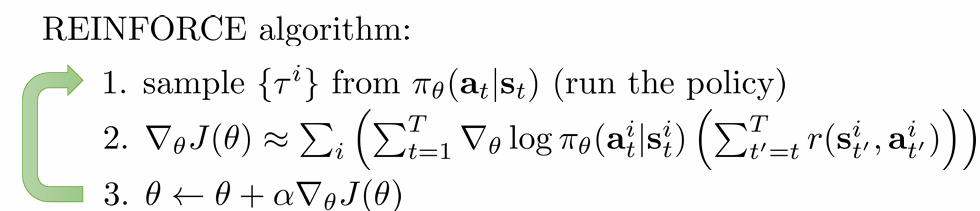[CS285] Ch6. Actor-Critic Algorithms

YJ·2025년 1월 22일

CS 285 DRL Deep Reinforcement Learning RL

CS 285

목록 보기

3/6

Deep Reinforcement Learning을 소개하는 Berkely CS 285 강좌의 Ch4~Ch9를 들으며 제 지식과 함께 정리해보고자 합니다. 강의 링크는 아래를 참고하세요.

https://rail.eecs.berkeley.edu/deeprlcourse/

제 나름의 지식을 많이 덧붙여 틀린 부분이 있을 수 있습니다. 발견하시면 댓글로 지적 부탁드립니다!
이해가 안되는 경우 질문도 환영입니다!

Ch6. Actor-Critic Algorithms

Actor-Critic Algorithm의 경우 policy-based method와 value-based method를 합친 것이라고 언급하기도 합니다. Actor(=policy)와 Critic(=value function) 둘 다를 학습하는 방법이기 때문입니다. 이 강의에서는 value-based method를 배우기 전, policy gradient의 연장선에서 actor-critic 알고리즘을 소개합니다.(실제로 그게 맞기도 하고..) 지난 강의의 내용을 기억해야 따라올 수 있으니, 이해가 잘 되지 않는다면 지난 포스팅을 확인해주세요!

improving policy gradients

policy gradients

지난 시간 배운 policy gradient의 대표 알고리즘 REINFORCE는 다음과 같습니다.

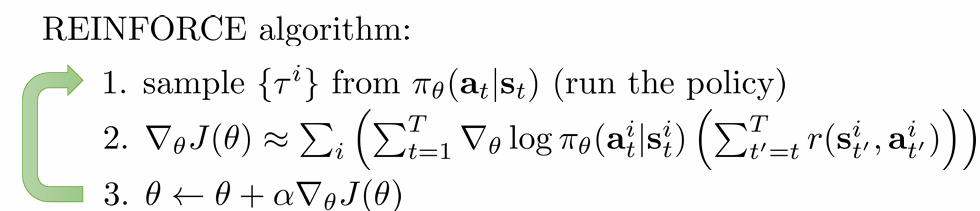
여기서 계산한 objective function의 gradient 추정치는 다음과 같습니다.

\nabla_\theta J(\theta) \approx \frac{1}{N} \displaystyle\sum_{i=1}^{N} \displaystyle\sum_{t=1}^{T}{\nabla_\theta \log{\pi_\theta(a_{i,t}|s_{i,t})}} \left(\displaystyle\sum_{t'=t}^{T}{r(s_{i,t'},a_{i,t'})} \right) = \frac{1}{N} \displaystyle\sum_{i=1}^{N} \displaystyle\sum_{t=1}^{T}{\nabla_\theta \log{\pi_\theta(a_{i,t}|s_{i,t})}} \hat{Q}_{i,t}

이 때 사용하는 reward는 "reward to go"로, time step t에서의 action은 그 이후의 reward에만 영향을 미치기 때문에(causality) 이 값을 사용한다고 하였습니다. Causality를 적용하면 합리적일 뿐만 아니라 variance도 줄일 수 있다고 언급했었습니다.

그러나 이 때 사용하는 "reward to go"는 Q function의 single sample estimate일 뿐입니다.

자세히 설명하자면, 우선 Q fucntion의 정의는 다음과 같았습니다.

Q^\pi(s_t,a_t) = \sum_{t'=t}^{T} E_{\pi_\theta}[r(s_{t'},a_{t'})|s_t,a_t]

그렇다면 우리가 계산한 $\hat{Q}_{i,t}$ 는, state $s_t$ 에서 action $a_t$ 를 취했을 때 앞으로 얻게 될 reward의 기댓값인 $Q(s_t,a_t)$ 를 추정하는 하나의 sample일 뿐이라는 것이죠. 그렇다면 우리가 어떤 sample을 추출했느냐에 따라서 $\hat{Q}_{i,t}$ 값은 매우 달라질 수도 있을 거고, 이는 high variance를 야기하는 문제가 됩니다.

improving estimate

이러한 문제를 해결하기 위해, single sample estimate인 $\hat{Q}(s_t,a_t)$ 를 사용하지 않고, 아예 $Q(s_t,a_t)$ 를 사용하는 방법을 생각해볼 수 있습니다. 그 경우 gradient 추정치는 다음과 같은 식으로 변하게 됩니다.

\nabla_\theta J(\theta) \approx \frac{1}{N} \displaystyle\sum_{i=1}^{N} \displaystyle\sum_{t=1}^{T}{\nabla_\theta \log{\pi_\theta(a_{i,t}|s_{i,t})}} Q(s_{i,t},a_{i,t})

그렇다면 우리는 variance를 낮출 수 있게 될 것입니다.

지난 시간 variance를 낮추기 위해 unbiased baseline을 사용했었습니다. 다음과 같이 좋은 unbiased baseline으로 return의 평균을 언급했었습니다.

b = \frac{1}{N} \displaystyle\sum_{i=1}^{N}{\displaystyle\sum_{t'=1}^{T} r(s_{i,t'},a_{i,t'})}

지금은 $Q(s_t,a_t)$ 를 estimator로 사용하고 있으니, baseline으로 다음과 같은 $Q(s_t,a_t)$ 의 평균치를 사용하는 방법을 생각해볼 수 있습니다.

b_t = \frac{1}{N} \sum_{i} Q(s_{i,t},a_{i,t})

그런데 value function의 정의는 같은 state에 대해 가능한 모든 action에 대한 Q의 기댓값이었으므로, 우리는 결국 value function을 baseline으로 사용하면 된다는 것을 알게 됩니다.

V^\pi(s_t) = E_{a_t \sim \pi_\theta(a_t|s_t)}[Q^\pi(s_t,a_t)]

그러면 우리의 식은 advantage function의 정의에 의해 다음과 같이 간단하게 정리됩니다.

\nabla_\theta J(\theta) \approx \frac{1}{N} \displaystyle\sum_{i=1}^{N} \displaystyle\sum_{t=1}^{T}{\nabla_\theta \log{\pi_\theta(a_{i,t}|s_{i,t})}} \left(Q^\pi(s_{i,t},a_{i,t}) -V^\pi(s_{i,t}) \right) = \frac{1}{N} \displaystyle\sum_{i=1}^{N} \displaystyle\sum_{t=1}^{T}{\nabla_\theta \log{\pi_\theta(a_{i,t}|s_{i,t})}} A^\pi(s_{i,t},a_{i,t})

what to fitting

식이 간단해졌으니 이제 advantage function 부분을 fitting할 차례입니다. 우리는 value function, q-function, advantage function 3개의 선택지를 가지고 있습니다. 결론부터 말씀 드리면 우리는 value function을 fitting할 것입니다. Value function은 state에만 의존하기 때문에 다른 function보다 input parameter가 적어 학습에 더 유리하기 때문입니다.

value function을 사용하기 위해서 식을 변형해야 합니다. 우선 Q-function의 정의는 다음과 같았습니다.

\begin{aligned} Q^\pi(s_t,a_t) &= \sum_{t'=t}^{T} E_{\pi_\theta}[r(s_{t'},a_{t'})|s_t,a_t] \\ &= r(s_t,a_t) + \sum_{t'=t+1}^{T} E_{\pi_\theta}[r(s_{t'},a_{t'})|s_t,a_t] \end{aligned}

두번째 등호는 one-step 전개를 했을 때, $r(s_t,a_t)$ 가 정해진 값이기 때문에 성립합니다. 뒤의 기댓값 항은 결국 time step $t+1$ 부터의 reward의 합이 되니, $V(s_{t+1})$ 의 기댓값이라고 볼 수 있습니다. 우리는 우리가 관측한 $s_{t+1}$ 에서의 value function값인 $V(s_{t+1})$ 로 이 기댓값을 추정해볼 수 있고, 따라서 advantage function을 다음과 같이 $V$ 에 관한 식으로 전개해볼 수 있습니다.

A^\pi(s_t,a_t) = Q^\pi(s_{t},a_{t}) -V^\pi(s_{t}) \approx r(s_t,a_t) + V^\pi(s_{t+1}) - V^\pi(s_{t})

그러면 우리는 이제 value function만 fitting할 수 있게 되었습니다. single sample estimate를 피하다가 결국에는 value function만 사용하기 위해 쓰는 게 조금 모순적이긴 하지만, return 전체를 single sample estimate 하는 것보단 낫다~ 라고 보시면 될 거 같습니다.

policy evaluation(fitting value function)

그렇다면 어떻게 value function을 fitting할 수 있을까요? 일단 policy와는 다른 neural network를 준비하고, 그 parameter를 $\phi$ 라고 합시다. 어떤 목적함수를 어떤 값에 fitting해야 할까요?

우선 늘 그랬듯 Monte Carlo Evaluation을 사용하는 방법이 있습니다. 다음 식처럼 sample을 많이 수집해서 평균값을 내는 것이죠.

V^\pi(s_t) \approx \frac{1}{N} \sum_{i=1}^{N} \sum_{t'=t}^{T} r(s_{i,t'},a_{i,t'})

그러나 현실적으로 이렇게 sample을 수집하는 것은 불가능합니다. 이런 방식으로 샘플을 수집하기 위해서는 time step t에서 특정 state $s_t$ 에 도달해야 하는데 현실적인 model-free 방법론에서는 state를 특정 state로 유도하는 게 불가능에 가깝기 때문입니다. (현실적인 state가 대부분 continuous하거나 space가 매우 방대하고, 우리는 policy대로 수행해 모르는 transition function으로 인해 다음 state를 얻기 때문)

따라서 우리는 다른 방법을 사용해야 합니다. 다음과 같은 single sample estimate를 봅시다.

V^\pi(s_t) \approx \sum_{t'=t}^{T} r(s_{i,t'},a_{i,t'})

이 estimate를 target으로 하는 다음과 같은 train data를 만들 수 있습니다.

training \ data = \left\{ \left( s_{i,t}, y_{i,t} = \sum_{t'=t}^{T} r(s_{i,t'},a_{i,t'}) \right) \right\}

그러면 이 data에 대해 다음과 같은 batch를 이용한 loss function을 정의할 수 있습니다. single sample estimate보단 훨씬 정확할 것입니다.

\mathcal{L} (\phi) = \frac{1}{2} \sum_{i} { \begin{Vmatrix} \hat{V}_\phi^\pi(s_{i,t})-y_{i,t} \end{Vmatrix}^2 }

또는 value function을 한 번 전개하여 training data를 구성할 수 있습니다. Value function을 single sample estimate를 이용해 한 번 전개하면 다음과 같습니다.

V^\pi(s_t) = \sum_{t'=t}^{T} E_{\pi_\theta}[r(s_{t'},a_{t'})|s_t] \approx r(s_t,a_t)+ \sum_{t'=t+1}^{T} E_{\pi_\theta}[r(s_{t'},a_{t'})|s_t] = r(s_t, a_t) + V^\pi(s_{t+1})

이 때 현재의 network로 구한 $V^\pi(s_{t+1})$ 를 다음과 같이 estimate에 사용한다는 것입니다. 따라서 training data는 다음과 같이 구성됩니다. loss function은 동일합니다.

training \ data = \left\{ \left( s_{i,t}, y_{i,t} = r(s_{i,t}, a_{i,t}) + V^\pi_\phi(s_{i, t+1}) \right) \right\}

$V$ 를 fitting하는 데에 $V$ 를 사용했기 때문에 이 방법을 bootstrapped estimate이라고 부릅니다.

From evaluation to Actor-Critic

Actor-Critic Algorithm

이렇게 구성한 actor-critic 알고리즘은 위와 같습니다. REINFORCE에서 $V_\phi$ 를 fit하여 $A^\pi$ 를 추정하는 식이 추가된 것 뿐입니다.

그런데 $V_\phi$ 를 fit하는 과정에서 infinite horizon case의 경우 문제가 생기게 됩니다. 우선 loss function을 다시 보면 다음과 같습니다.

\mathcal{L} (\phi) = \frac{1}{2} \sum_{i} { \begin{Vmatrix} \hat{V}_\phi^\pi(s_{i,t})-y_{i,t} \end{Vmatrix}^2 }

마지막에 배운 bootstrapped estimate의 경우 다음과 같이 target을 설정합니다.

y_t \approx r(s_t, a_t) + V^\pi(s_{t+1})

그렇다면 reward가 계속 양수라면 어떻게 될까요? $V$ 값에 양수인 reward를 더하고, 그것을 target으로 fitting하고, 다시 target을 만들고... 그러면 $V$ 는 무한정 커지게 될 것입니다. Infinite horizon case에서는 이런 일이 빈번히 일어납니다.

이를 해결하기 위해서는 미래의 reward일수록 적게 고려하는 방식을 이용할 수 있습니다. 이렇게 정의되는 것이 discount factor입니다.

discount factor

discount factor는 현재 time step t에서 한 time step씩 미래로 갈 때마다 reward를 적게 고려하는 정도 $\gamma$ 를 나타냅니다. ( $\gamma \in [0,1]$ ) 이를 반영하여 target을 다시 설정하면 다음과 같습니다.

y_t \approx r(s_t, a_t) + \gamma V^\pi(s_{t+1})

$\gamma$ 를 반영하는 것은 다음과 같이 MDP에 death state 하나를 더 추가하는 것과 같습니다.(개념적 설명, 실제로 추가되는 것은 아님)

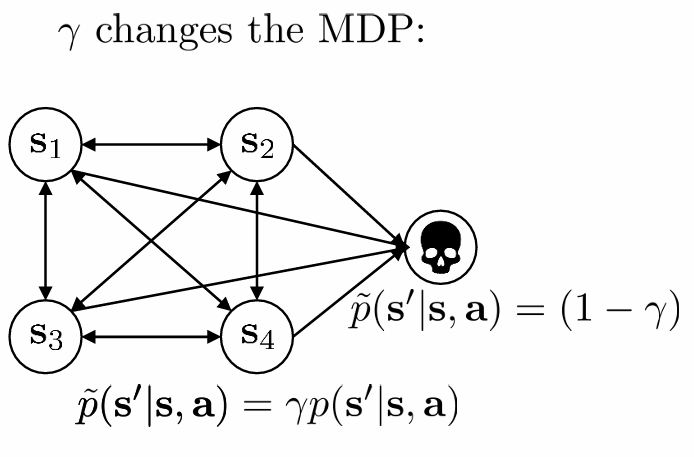
각 state가 $1-\gamma$ 만큼의 확률로 reward가 0인 death state로 전이되니, 기존의 reward에 $\gamma$ 가 곱해지게 되는 것입니다.

그러면 fitting하는 값 뿐만 아니라, gradient도 다음과 같이 변하게 됩니다.

\nabla_\theta J(\theta) \approx \frac{1}{N} \displaystyle\sum_{i=1}^{N} \displaystyle\sum_{t=1}^{T}{\nabla_\theta \log{\pi_\theta(a_{i,t}|s_{i,t})}} \left( r(s_t,a_t) + \gamma \hat{V}_\phi^\pi(s_{t+1}) - \hat{V}_\phi^\pi(s_{t}) \right)

discount factor for policy gradient

discount factor를 뒤늦게 도입했기 때문에 policy gradient에서 이를 어떻게 사용하는지 잠시 짚고 넘어갑시다. Monte Carlo Evaluation을 사용하는 policy gradient의 경우 gradient가 다음과 같았습니다. infinite horizon case에서는 당연히 reward의 합이 무한대로 발산하는 경우가 많이 생기겠죠.

\nabla_\theta J(\theta) \approx \frac{1}{N} \displaystyle\sum_{i=1}^{N} \displaystyle\sum_{t=1}^{T}{\nabla_\theta \log{\pi_\theta(a_{i,t}|s_{i,t})}} \left(\displaystyle\sum_{t'=t}^{T}{r(s_{i,t'},a_{i,t'})} \right)

time step에 따라 $\gamma$ 를 지수적으로 곱하는 데에는 다음 두 가지 방법이 있습니다.

option \ 1: \nabla_\theta J(\theta) \approx \frac{1}{N} \displaystyle\sum_{i=1}^{N} \displaystyle\sum_{t=1}^{T}{\nabla_\theta \log{\pi_\theta(a_{i,t}|s_{i,t})}} \left(\displaystyle\sum_{t'=t}^{T}{\gamma^{t'-t} r(s_{i,t'},a_{i,t'})} \right) \\ option \ 2: \nabla_\theta J(\theta) \approx \frac{1}{N} \displaystyle\sum_{i=1}^{N} \displaystyle\sum_{t=1}^{T}{\nabla_\theta \log{\pi_\theta(a_{i,t}|s_{i,t})}} \left(\displaystyle\sum_{t'=t}^{T}{\gamma^{t'-1} r(s_{i,t'},a_{i,t'})} \right)

$option \ 1$ 은 reward를 곱할 때 매 time step $t$ 를 기준으로 $\gamma$ 를 곱하는 것입니다. $option \ 2$ 는 initial state를 기준으로 $\gamma$ 를 곱하는 것입니다. $option \ 2$ 를 $option \ 1$ 에 맞춰 전개해보면 다음과 같습니다.

option \ 2: \nabla_\theta J(\theta) \approx \frac{1}{N} \displaystyle\sum_{i=1}^{N} \displaystyle\sum_{t=1}^{T}{\gamma^{t-1} \nabla_\theta \log{\pi_\theta(a_{i,t}|s_{i,t})}} \left(\displaystyle\sum_{t'=t}^{T}{\gamma^{t'-t} r(s_{i,t'},a_{i,t'})} \right)

이를 해석해보면 매 time step에서 reward를 고려할 때 discount factor를 고려할 뿐만 아니라, 나중 time step이 될 수록 gradient 자체를 적게 고려한다는 뜻이 됩니다. 지나치게 미래의 일을 고려하지 않는 것은 꽤 합리적으로 보입니다.

하지만 우리는 infinite horizon case에서, 현재의 행동이 매우 이후의 reward에 미칠 영향을 줄이고 싶은 것 뿐이지, 매우 나중에는 아무렇게나 행동하게 만들고 싶은 게 아닙니다. 따라서 우리는 고려하는 time step에 따라 $\gamma$ 를 상대적으로 적용하는, 즉 reward에만 적용하는 방법을 훨씬 선호합니다. 이는 actor-critic에 적용된 $\gamma$ 와도 일맥상통합니다.

discount factor가 들어간 batch actor-critic algorithm은 위와 같습니다.

Actor-Critic design decision

actor-critic 알고리즘을 실제로 design하는 데 고려해야할 점들을 살펴봅시다.

architecture design

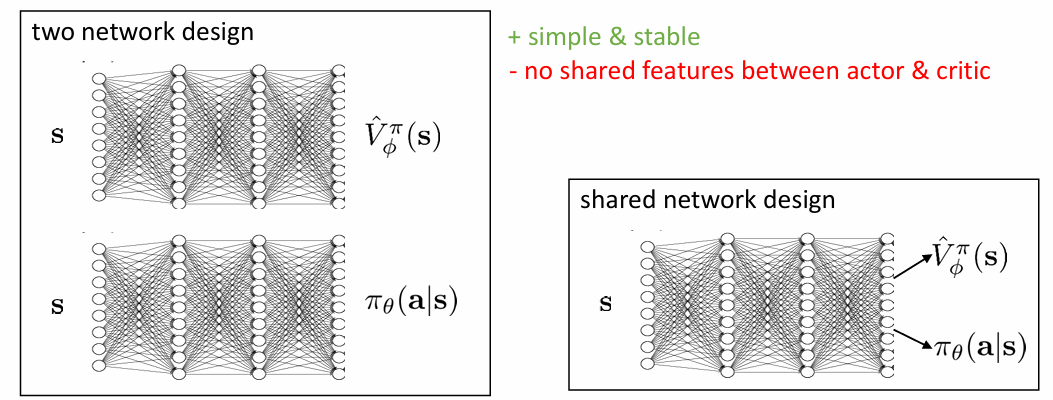
우리가 학습해야할 것은 actor(policy)와 critic(value function) 두 가지입니다. 이 두 가지의 parameter를 network 하나로 design할 것인지 두 가지로 design할 것인지를 우선 선택해야 합니다. 두 개로 디자인하는 경우 간단하고 안정적이지만, 결국 같은 state에 대해 작동하는 actor와 critic 사이에 어떤 상관관계를 고려하지 않고 두 네트워크를 학습해야 합니다. 하나로 디자인하는 경우 둘의 상관관계를 고려할 수 있으나 두 개가 반대로 학습되려고 한다거나 하는 문제가 발생할 수 있어 불안정하고 복잡해집니다.

online vs offline

다음은 online learning을 사용할 것인지 offline learning을 사용할 것인지를 정해야 합니다. 먼저 두 개의 정의를 살펴보겠습니다.

online learning: 환경과 agent가 직접 상호작용하여 data를 계속해서 수집할 수 있는 경우 online learning이라고 합니다.
offline learning: 환경과 agent가 직접 상호작용할 수 없어 정해진 data로 학습해야 하는 경우 offline learning이라고 합니다.

이는 on-policy, off-policy와 떼어놓을 수 없는 개념인데요, 정리해보면 아래 표와 같습니다.

online learning은 data를 계속해서 수집한다면 어떤 policy를 쓰든 상관 없으므로 on-policy와 off-policy 둘 다 가능하지만, offline learning은 dataset이 고정되어 있으므로 현재의 policy로 data를 매번 수집하는 게 불가능합니다. 따라서 off-policy일 수밖에 없습니다.

online 으로 작성된 actor-critic 알고리즘은 다음과 같습니다.

online actor-critic 알고리즘을 보면 매번 환경과 한 번 상호작용을 하고 그 데이터 하나로 gradient를 update합니다. batch actor-critic 알고리즘이 batch를 sample하여 gradient를 update하는 것과는 다르죠.

여기서 굉장히 헷갈리는 부분은, batch actor critic도 online일 수 있고, online actor-critic도 배치 단위로 작동할 수 있다는 것입니다. batch actor critic의 경우에도 환경과 지속적으로 상호작용하면서 data를 수집할 수 있고, online actor-critic도 여러 환경을 동시에 돌려 batch 단위로 학습을 진행할 수 있기 때문입니다. 두 알고리즘은 무엇을 강조하느냐의 차이일 뿐, 배타적인 개념이 아닙니다. 다만 여기서는 online actor-critic을 한 번의 data 수집으로 updtae, batch를 여러번의 data 수집으로 update하는 방식으로 구분하는듯 합니다. 바로 다음에 배울 부분에서 헷갈릴 수 있어 언급하였습니다.

online, on-policy algorithm

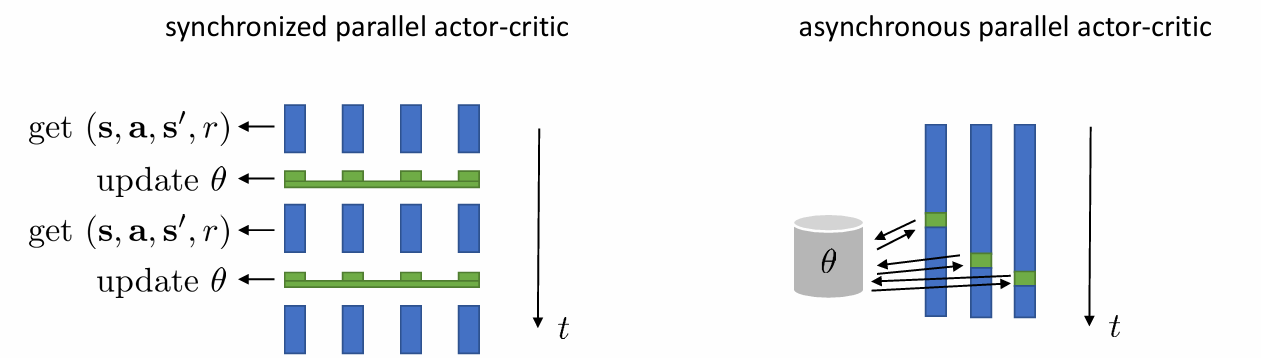
online actor-critic도 batch 단위로 작동할 수 있다고 하였습니다. 위와 같이 여러 환경을 여러번 돌리면 가능하죠. 그런데 이 환경들을 synchronize할 것이냐 아니냐를 결정해야합니다. synchronize하면 문제는 없지만, 모든 환경을 동일하게 매번 끊으면서 가야하기 때문에 시간이 좀 더 걸립니다. asnchronous한 경우, 시간이 좀 덜 걸리지만 각 환경이 각자의 속도로 진행되어 한 batch에 있는 data 중 old policy로 수집된 data가 존재할 수 있습니다. 그러나 이정도의 약간의 차이로 발생하는 bias는 감수할 정도라고 합니다.

online, off-policy algorithm

old policy로 수집된 data가 존재하는 게 문제가 된다면 off-policy는 어떻게 가능할까요? 현재 policy도 아닌 다른 policy로 뽑은 data를 이용하는데 말이죠. off-policy online actor-critic이 가능할까요? 우선 기존의 알고리즘을 off-policy 형태로 작성해보면 잘못된 부분이 두 부분 있습니다.

문제는 fitting을 할 때 발생합니다. 우리는 actor와 critic 두가지를 fitting하니 두 부분에서 문제가 발생하게 됩니다.

critic fitting

먼저 $y_i=r_i+\gamma \hat{V}_\phi^\pi(s_i')$ 에는 어떤 문제가 있을까요? action $a_i$ 는 현재 policy로 부터 나온 action이 아니기 때문에 이로 인한 transition으로 발생한 $s_i'$ 로 $\hat{V}_\phi^\pi(s_i')$ 를 구하여 $\hat{V}_\phi^\pi(s_i)$ 의 target value로 사용하는 것은 틀린 식입니다.

action 자체가 현재 policy로부터 나온 action이 아닌 것이 문제였으니, state와 action이 둘 다 주어진다고 생각하고 fitting을 해야 합니다. 이 때 이용할 것은 action 자체도 input으로 받는 Q-function입니다. Q-function을 one step 전개를 하면 다음과 같습니다.

\begin{aligned} Q^\pi(s_t,a_t) &= \sum_{t'=t}^{T} E_{\pi_\theta}[r(s_{t'},a_{t'})|s_t,a_t] \\ &= r(s_t,a_t) + \sum_{t'=t+1}^{T} E_{\pi_\theta}[r(s_{t'},a_{t'})|s_t,a_t] \\ &= r(s_t,a_t) + E_{s_{t+1} \sim p_\theta(s_{t+1}|a_t.s_t)}[V(s_{t+1})] \end{aligned}

이 때 $V(s_{t+1})$ 의 기댓값은 우리가 관측한 하나의 $V(s_{t+1})$ 로 추정할 수 있고 이는 다시 우리가 관측한 $Q(s_{t+1},a_{t+1})$ 로 추정할 수 있습니다. 이 때 $a_{t+1}$ 은 현재의 policy로 추출하게 됩니다. 그러면 off-policy learning에서 discount factor를 고려한 $\hat{Q}_\phi^\pi(s_t,a_t)$ 의 target은 다음과 같아집니다.

y_i=r_i+\gamma \hat{Q}_\phi^\pi(s_i',a_i')

실제로는 advantage function 대신 구한 q-function을 direct하게 사용합니다. baseline이 없으니 higher variance가 문제가 되겠지만, $\hat{Q}_\phi^\pi(s_i',a_i')$ 에서 action은 시뮬레이션 없이 우리 policy에서 많이 뽑기만 하면 되니 쉽게 추정 값의 개수를 늘릴 수 있고 그리하여 variance를 낮출 수 있기 때문입니다.

actor fitting

그렇다면 $\nabla_\theta \log{\pi_\theta(a_{i}|s_{i})}$ 에는 어떤 문제가 있을까요? 애초에 이 policy로 뽑은 action이 아니니 $\pi_\theta$ 가 실행되었다고 할 수 없고, 따라서 이것은 잘못된 gradient입니다. ch5에서는 이 문제를 importance sampling으로 해결했었습니다.

\nabla_{\theta'} J(\theta') = E_{\tau \sim p_{\theta}(\tau)}\left[\frac{p_{\theta'}(\tau)}{p_\theta(\tau)} \nabla_{\theta'} \log{p_{\theta'}(\tau)} r(\tau)\right]

여기서는 더 좋은 해결법을 소개합니다. 바로 data의 action을 사용하지 않고, 현재의 policy에서 action $a_t^\pi$ 를 뽑아 식에 넣는 것이죠. 그러면 gradient는 다음과 같이 정리됩니다.(Q를 fit하는 과정은 gradient를 fit하는 과정과 완전히 분리됩니다. Q를 fit하는 과정에서는 data를 그대로 사용합니다. 여기서 사용하는 Q는 fitting 후의 Q입니다.)

\nabla_\theta J(\theta) \approx \frac{1}{N} \displaystyle\sum_{i=1}^{N} \displaystyle\sum_{t=1}^{T}{\nabla_\theta \log{\pi_\theta(a_{i,t}^\pi|s_{i,t})}} \hat{Q}(s_{i,t},a_{i,t}^\pi)

이렇게 고쳐진 알고리즘은 다음과 같습니다.

여기서 $s_i$ 자체가 $p_\theta$ 의 분포를 따르지 않는다는 문제가 있긴 하지만.. 그 정도는 받아들일 수 있습니다. 분포가 아예 겹치지 않는 것이 아니니, 우리는 오히려 중요한 stuff를 놓치지 않으면서도 broader한 distribution의 data를 얻을 수 있기 때문입니다.

Critics as baselines

우리는 value function을 critics라고 했었습니다. Actor-critic이 아닌 policy gradient로 돌아가서, baseline을 학습시키는 policy gradient 방법을 소개합니다. 학습한 value function이 baseline으로만 쓰이는 경우는 actor-critic이라고 부르지는 않습니다.

value-function baseline

policy gradient의 gradient는 다음과 같았습니다. Unbiased된 baseline으로 variance를 낮추었지만 여전히 single sample estimation으로 variance가 높은 편이었죠.

\nabla_\theta J(\theta) \approx \frac{1}{N} \displaystyle\sum_{i=1}^{N} \displaystyle\sum_{t=1}^{T}{\nabla_\theta \log{\pi_\theta(a_{i,t}|s_{i,t})}} \left( \left(\displaystyle\sum_{t'=t}^{T}{\gamma^{t'-t} r(s_{i,t'},a_{i,t'})} \right) -b \right)

actor-critic의 gradient는 다음과 같았습니다. Variance는 훨씬 낮추었지만 critic이 정확하지 않기 때문에 biased 되었다는 문제점이 있었습니다.

\nabla_\theta J(\theta) \approx \frac{1}{N} \displaystyle\sum_{i=1}^{N} \displaystyle\sum_{t=1}^{T}{\nabla_\theta \log{\pi_\theta(a_{i,t}|s_{i,t})}} \left( r(s_{i,t},a_{i,t}) + \gamma \hat{V}_\phi^\pi(s_{i,t+1}) - \hat{V}_\phi^\pi(s_{i,t}) \right)

두 식을 합쳐 장점만 가져올 수 있는 방법이 있을까요? 다음과 같이 식을 써볼 수 있겠습니다.

\nabla_\theta J(\theta) \approx \frac{1}{N} \displaystyle\sum_{i=1}^{N} \displaystyle\sum_{t=1}^{T}{\nabla_\theta \log{\pi_\theta(a_{i,t}|s_{i,t})}} \left( \left(\displaystyle\sum_{t'=t}^{T}{\gamma^{t'-t} r(s_{i,t'},a_{i,t'})} \right) -\hat{V}_\phi^\pi(s_{i,t}) \right)

Baseline으로만 학습한 critic을 사용하는 것입니다. Baseline으로만 사용했으니 bias가 없고, 대신 reward에 더 가까운 값을 빼니(baseline으로 batch의 reward 평균이 아니라 각각의 state에 대한 value function 값을 썼으니) variance는 낮아지죠. 그런데 variance를 더 낮출 수 있는 방법이 있습니다. 바로 q-function을 baseline으로 사용하는 것입니다.

Q-function baseline

Q-function을 baseline으로 사용하면 식이 다음과 같이 변화합니다.

\nabla_\theta J(\theta) \approx \frac{1}{N} \displaystyle\sum_{i=1}^{N} \displaystyle\sum_{t=1}^{T}{\nabla_\theta \log{\pi_\theta(a_{i,t}|s_{i,t})}} \left( \left(\displaystyle\sum_{t'=t}^{T}{\gamma^{t'-t} r(s_{i,t'},a_{i,t'})} \right) -Q_\phi^\pi(s_{i,t},a_{i,t}) \right)

Q는 $s, a$ 를 모두 input으로 받으니 Q값이 정확하면 정확할수록 data의 return에 매우 가까워질 것입니다. 그러면 variance는 매우 작아지겠죠. 그러나 이 식은 틀린 식입니다.

Q를 baseline으로 쓰면 다음과 같은 error term이 생깁니다.

\nabla_\theta J(\theta) \approx \frac{1}{N} \displaystyle\sum_{i=1}^{N} \displaystyle\sum_{t=1}^{T}{\nabla_\theta \log{\pi_\theta(a_{i,t}|s_{i,t})}} \left( \left(\displaystyle\sum_{t'=t}^{T}{\gamma^{t'-t} r(s_{i,t'},a_{i,t'})} \right) -Q_\phi^\pi(s_{i,t},a_{i,t}) \right) + \frac{1}{N} \displaystyle\sum_{i=1}^{N} \displaystyle\sum_{t=1}^{T}{\nabla_\theta }E_{a \sim \pi_\theta(a_t|s_t)}[ Q_\phi^\pi(s_{i,t},a_{i,t})]

강의에서 이유는 설명해주지 않는데, 원래 둘 다 $\theta$ 에 관한 식이 곱해져 있을 때 미분하게 되면 하나씩 미분한 걸 더하듯이, baseline이 Q가 되면 Q가 $\theta$ 에 관한 식이 되어서 error term이 생겼다 보시면 될 거 같습니다. ( $V$ 와 달리 $Q$ 는 $\pi_\theta$ 에서 뽑은 $a_t$ 에 의존하므로...)

Further Algorithms

n-step return Actor-Critic

그런데 critic을 baseline으로 사용하는 방법은 여전히 single sample estimate를 취하기 때문에 variance가 높습니다. 그렇다면 다음과 같이 n-step까지만 실제 실험으로 얻은 reward를 사용하고 나머지는 value function을 통해 예측하면 어떨까요?

\nabla_\theta J(\theta) \approx \frac{1}{N} \displaystyle\sum_{i=1}^{N} \displaystyle\sum_{t=1}^{T}{\nabla_\theta \log{\pi_\theta(a_{i,t}|s_{i,t})}} \left( \left(\displaystyle\sum_{t'=t}^{t+n}{\gamma^{t'-t} r(s_{i,t'},a_{i,t'})} \right) +\gamma^n \hat{V}_\phi^\pi(s_{i,t+n}) -\hat{V}_\phi^\pi(s_{i,t}) \right)

value function을 사용하여 variance를 낮추면서도 실제 reward를 이용하여 value function의 bias를 낮추었습니다 이게 n-setp return actor-critic입니다.

GAE(Generalized Advantage Estimation)

그런데 n-step return은 우리가 n을 선택해야 한다는 문제가 있습니다. 그렇다면 다음과 같이 모든 n에 대해 구한 값을 적절히 weighted sum하면 어떨까요?

\hat{A}^\pi_n (s_t, a_t) = \left(\displaystyle\sum_{t'=t}^{t+n}{\gamma^{t'-t} r(s_{i,t'},a_{i,t'})} \right) +\gamma^n \hat{V}_\phi^\pi(s_{i,t+n}) -\hat{V}_\phi^\pi(s_{i,t})

\hat{A}^\pi_{GAE} (s_t, a_t) = \sum_{n=1}^{\infty}w_n \hat{A}^\pi_n (s_t, a_t)

weight는 다음과 같이 discount factor와 함께 적용되는 방식으로 주어집니다.

w_n \propto \lambda^{n-1}

\delta_{t'} = r(s_{t'},a_{t'}) +\gamma \hat{V}_\phi^\pi(s_{t'+1}) -\hat{V}_\phi^\pi(s_{t'})

\hat{A}^\pi_{GAE} (s_t, a_t) = \sum_{t'=t}^{\infty} (\gamma \lambda)^{t'-t}\delta_{t'}

이로서 ch6에 대한 포스팅이 끝났습니다. Example이나 further reading에 관한 부분은 생략하였으니, 강의를 참고하시면 될 거 같습니다. 틀린 부분이나 이해가 안된 부분이 있다면 댓글 주세요!

CS285 website: https://rail.eecs.berkeley.edu/deeprlcourse/

online, offline learning 참고: https://jebeom.github.io/fundamental/policy_diff/