Deep Reinforcement Learning을 소개하는 Berkely CS 285 강좌의 Ch4~Ch9를 들으며 제 지식과 함께 정리해보고자 합니다. 강의 링크는 아래를 참고하세요.

https://rail.eecs.berkeley.edu/deeprlcourse/

제 나름의 지식을 많이 덧붙여 틀린 부분이 있을 수 있습니다. 발견하시면 댓글로 지적 부탁드립니다!
이해가 안되는 경우 질문도 환영입니다!

Ch7. Value Function Methods

Basic value function methods

basic idea of value function methods

ch4, ch5에서 배운 policy gradient 알고리즘과 actor-critic 알고리즘의 핵심은 RL의 objective function을 최대화하는 데 gradient ascent를 사용한다는 것이었습니다. 여기서 gradient를 어떻게 추정할 것인가, 어떻게 잘 작동하게 할 것인가(bias와 variance의 관점에서)에 따라 알고리즘의 차이가 있었을 뿐, policy의 parameter를 update한다는 점은 변하지 않았습니다.

그러나 actor-critic을 막상 배우고 나니, $V$를 fitting하고 그걸로 다시 policy gradient를 수행하는 게 비효율적으로 느껴집니다. 왜냐하면 이미 advantage function이 state에서 좋은 action이 무엇인지에 대한 정보를 담고있기 때문입니다. 그렇다면 지금까지 배운 알고리즘처럼 policy를 soft하게 update할 필요 없고, state에서 advantage function의 값이 가장 높은 action을 취하도록 hard한 update를 해도 되지 않을까요? 이것이 바로 value-based method의 기본 원리입니다.

(여기서 제가 쓴 soft한 update라는 것은 policy gradient의 기본 원리를 의미합니다. Policy gradient의 기본 원리는 policy가 좋은 action을 선택할 확률은 늘리고 나쁜 action을 선택할 확률은 줄이며 점진적으로 나아가는 것이었죠. Value-based는 이와 달리 hard한 방식을 취합니다. Policy가 stochastic한 게 아니고 deterministic하게 그냥 좋은 action만 취하게끔 하자는 것이죠.)

policy iteration method

위의 원리를 그대로 쓰되, explicit한 policy를 우선 남겨두는 게 policy iteration method입니다.

algorithms

알고리즘은 다음과 같습니다.

아주 단순합니다. $A^\pi$를 evaluate하고, 그것을 argmax하여 policy를 udpate합니다. Continuous한 action space를 가지는 경우 argmax 자체가 또 하나의 큰 문제가 될 수 있는데, 이는 이후의 강의에서 다룹니다.

이 알고리즘엔 중요한 부분이 빠져있습니다. $A^\pi$를 어떻게 evaluate할까요? $A^\pi$를 정의에 의해 전개해보면 다음과 같았습니다. 이는 actor-critic에서 value function을 fitting하는 이유를 설명하며 나오기도 한 식입니다.

그러면 $V$를 알면 $Q$도 $A$도 계산할 수 있습니다. $V$는 state에만 의존하기 때문에 input이 적어 학습할 parameter가 비교적 적어지고 따라서 더 효율적인 학습을 할 수 있다고 했었습니다.

policy iteration algorithm with dynamic programming

Neural network를 학습하여 $V$를 evaluate하는 복잡한 방법 말고, 아주 단순한 방법을 통해서 살펴보도록 하겠습니다. 그러기 위해선 우선 다음과 같은 두 가지 전제가 필요합니다. 일반적인 model-free 알고리즘에서 말도 안되는 가정이므로 후에 이것을 확장합니다.

• transition probability $p(s'|s,a)$를 알고 있다.
• state와 action space가 discrete하고 tabular로 표현할 수 있을 정도로 작다.

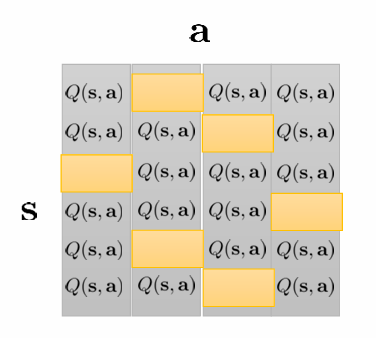
이게 무슨 뜻인지는 예시를 통해 살펴보도록 하겠습니다.

위와 같은 4*4 판 위에서 움직이는 agent가 있다고 해봅시다. 그러면 state는 16개, 상하좌우로 움직일 수 있으니 action은 4개가 될 것입니다. Transition operator $\mathcal{T}$는 $\mathcal{S} \times \mathcal{S} \times \mathcal{A}$ 차원을 가지니 $16 \times 16 \times 4$ tensor가 될 것입니다.

$V$를 one-step 전개하면 다음과 같습니다.

앞서 우리가 transition probability를 알고 있다고 가정했으므로 $E_{s_{t+1} \sim p(s_{t+1}|s_t,a_t)}[V(s_{t+1})]$를 쉽게 계산할 수 있습니다. 이것을 $\pi(a_t|s_t)$에 따라 모든 action에 대해서만 evaluate 하면 됩니다. 그런데 우리는 stochastic한 policy가 아니라 다음과 같이 state 하나에 대해 action 하나가 정해지는 deterministic한 policy를 사용하기로 했으므로, 식은 더 간단해집니다.

policy iteration을 정리하면 다음과 같습니다.

value iteration method

그런데 policy iteration 알고리즘에는 두 가지 비효율적인 부분이 보입니다.

첫번째는 explicit한 policy가 필요하냐는 것입니다. 그냥 value function만 table에 저장해놓고 그때그때 argmax를 취하면 되는데 말이죠.

두번째는 꼭 advantage function을 써야하는 것입니다. Advantage function의 정의는 다음과 같았습니다.

우리는 정해진 state에 대해 $A$가 max가 되는 action을 찾는 것이므로 빼주는 $V^\pi(s_{t})$는 모든 action에 대해 동일합니다. 따라서 다음 식이 성립하고, 따라서 $A$를 쓸 필요 없이 $Q, V$만을 사용하는 되는 것입니다.

$Q$를 evaluate하는 것은 앞서 $A$를 evaluate 하는 데 사용했던 식을 이용합니다. Transition probability를 알고 있으니 $Q$를 evaluate 하는 식도 쉽게 계산할 수 있습니다.

Update한 $Q$를 앞선 경우처럼 table에 저장해두고, $V$는 정해진 s에서 $Q$에 max를 취하기만 하면 됩니다.

이렇게 새로 만든 value iteration method를 정리하면 다음과 같습니다.

Fitted Value iteration & Q-iteration

앞서 value function evaluation을 위한 두 가지 가정 중 두번째는, state와 action space가 discrete하고 small하다는 것이었습니다. 하지만 이는 보통의 경우에는 성립할 수 없는 가정입니다. 따라서 우리는 다른 방법을 사용해야합니다. 여기서 주로 채택되는 것이 neural network입니다.

fitted value iteration

Neural network를 이용해 value function을 표현하면, 매번 update 할 때마다 value function을 target값에 fitting하는 형태로 update 해야합니다. Target 값은 앞서 구한 값과 같은 걸 사용하면 되겠고, squared error를 줄이는 방향으로 학습하면 될 것입니다. 그리고 neural network의 input을 줄이기 위해 $Q$보단 $V$를 학습하는 것이 좋을 것입니다. 이렇게 정리한 fitted value iteration 알고리즘은 다음과 같습니다.

Max 값을 구하는 문제는 차치하고, 아직 해결하지 못한 문제가 있습니다. value function evaluation을 위한 첫번째 가정이 아직 필요합니다. 바로 $E[ V^\pi(s_{t+1})]$를 구하는 부분에서 transition probability가 필요합니다. 이 문제를 어떻게 해결할 수 있을까요?

가장 간단한 방법은 sample $(s, a, s', r)$을 통해 single sample approximation을 하는 것입니다. Expectation 대신에 우리가 구한 sample의 값 하나를 이용하는 것이죠. 그런데 single sample approximation은 정확하지 않으니, 조금 소극적으로 Q-function을 update하는 방법을 고려해보게 됩니다. 이것이 Q-iteration입니다.

Q-iteration

Value function 대신 Q-function을 update하면 무엇이 좋을까요? 두 function의 evaluation 식을 써보면 다음과 같습니다.

$Q$의 경우 원래 $Q^\pi(s_{t},a_{t}) = r(s_t,a_t) + \gamma E_{s_{t+1} \sim p(s_{t+1}|s_t,a_t)}[ V^\pi(s_{t+1})]$를 사용하는데, deterministic policy를 이용하므로 $V(s')$이 곧 $Q(s',\pi(s'))$이 되어 위와 같이 작성하였습니다.

두 식의 차이는 $a$가 $\pi$로부터 나왔느냐, 임의의 action이냐 입니다. 이 미묘한 차이가 아주 큰 차이를 만듭니다.

Value function을 fitting하게 되면 현재 policy로 뽑은 sample이 계속해서 필요하게 됩니다. 즉 policy가 조금이라도 변하면 sample을 모두 버려야합니다. 또한 초기화에 많은 영향을 받을 것입니다. 처음에 정해진 $\pi(s)$가 suboptimal한데, 그 action이 계속 뽑히게 되면 학습을 방해할 것입니다. 게다가 $V$는 input이 적은 대신 지나치게 함축적입니다. 최선의 action을 선택하기 위해서는 번거로운 절차가 필요합니다.

Q-function을 fitting하면 sample의 policy가 무엇이었느냐는 상관 없게 됩니다. Sample이 무작위로 수집된다면 여러 action을 탐색하여 optimal solution에 다가가기도 용이합니다. 또한 action에 대해 value를 독립적으로 학습할 수 있습니다. 이를 바로바로 정책으로 이용할 수 있게 됩니다. 따라서 우리는 Q-function을 업데이트하는 방식을 사용합니다.

이렇게 정리한 fitted Q-iteration 알고리즘은 다음과 같습니다. expectation에는 single sample estimation이 사용됩니다. $V(s')$에는 single sample $Q(s', \pi(s'))$이 사용됩니다.

그러나 안타깝게도 이 식은 NN과 같은 non-linear function approximation에 대해 수렴성을 보장하지 못합니다.

이 알고리즘에서 결정해야할 파라미터는 위와 같습니다.

우선 data를 얼마나 수집할지, 그리고 어떻게 수집할지를 정해야겠죠. 그리고는 iteration을 몇 번 할지, gradient step을 몇 번 할지 정해야 합니다. 여기서 gradient step이란 한 번의 gradient descent를 여러번 밟아 argmin에 최대한 도달시키는 것을 의미합니다.

From Q-iteration to Q-Learning

what is fitted Q-iteration optimizes?

앞서 살펴보았듯 Q-iteration algorithm은 꼭 policy로 수집한 sample을 필요로 하지 않습니다. off-policy 알고리즘이 가능하다는 뜻입니다.

fitted Q-iteration 알고리즘은 무엇을 optimize하고 있을까요? 이 알고리즘은 target과의 차이를 줄이는 쪽으로 parmeter를 update합니다. error term을 적어보면 다음과 같습니다.

만약 $\varepsilon = 0$이라면 우리는 진짜 $Q$를 구한 것이고, 이 function에 argmax를 취한 것이 optimal policy가 될 것입니다. 하지만 학습 중에는 error가 0이 아닙니다. 0이 아니라면 error는 policy가 얼마나 좋은지를 나타낸다기보다 그저 target고의 차이를 나타냅니다. Bootstrapped target을 이용하였기 때문입니다. Target이 optimal 한 값이 아니고 계속 변하게 됩니다.

online Q-iteration algorithms

fitted Q-iteration이 한 번의 data 수집과 한 번의 iteration과 한 번의 gradient step으로 이루어지면 이를 Q-learning이라고 부릅니다. 앞서 본 full fitted Q-iteration 알고리즘과 달리 online으로만 진행될 수 있기 때문에 online이라는 수식어가 붙은 것 같습니다. 알고리즘은 다음과 같습니다.

단 하나의 sample을 이용해 update를 진행합니다. 일반 fitted Q-iteration(offline)과 달리 parameter를 argmin이 아니라 error의 gradient를 취하여 gradient descent 하는 방식으로 update하고 있습니다. Offline의 경우도 neural network를 쓰면 optimizer에 따라 다르겠지만 어쨌든 gradient 방식을 취하는거 아니냐고 하실 수 있는데... 저도 그렇게 생각하긴 합니다만 강의에서는 우선 알고리즘에 차이를 둡니다.

Offline learning의 경우 무조건 off-policy이기 때문에 policy 선택이 자유롭지만, online learning의 경우 on-policy와 off-policy가 모두 가능합니다. 만약 Q-learning을 on-policy으로 해본다고 가정합시다. 그러면 다른 policy를 사용하지 않아도 되니 편리하겠죠. 학습이 끝난 뒤의 최종 policy는 다음과 같을 것입니다.

그런데 이 policy를 학습 중에도 이용하는 것은 좋지 않습니다. 현재의 $Q$가 optimal하지 않은데 이 $Q$에서의 최적 행동을 계속 뽑으면 우리는 실제로 좋은 action이 다른 action이어도 그 action에 대한 sample을 많이 얻지 못한 것이기 때문입니다. 강화학습에서 이 문제를 exploitation(현재 policy 이용)과 exploration(다른 action 탐색) 문제라고 하며, 이를 조절하기 위해 Q-learning에서는 다음과 같은 epsilon greedy, Boltzmann exploration 등을 사용합니다.

Value Functions in Theory

이 챕터는 부수적으로 이론적인 operator를 이용하여 value function method가 수렴성이 보장되지 않음을 보입니다.

Bellman Operator

Bellman Operator $\mathcal{B}$는 다음과 같이 정의됩니다. 복잡해 보이지만 그냥 이 operator를 적용하면, value iteration 알고리즘을 1회 수행한 것과 같아진다고 보시면 됩니다.

여기서 bellman operator를 계속 적용해서 fixed point $V^\star$에 도달했다고 해봅시다. 그러면 fixed point이기 때문에 다음이 성립하게 됩니다.

value iteration 알고리즘은 반드시 수렴합니다.(fitted value iteration은 아님. 뒤에 나옴) 이유는 $\mathcal{B}$가 contraction이기 때문입니다. Contraction은 다음과 같은 성질을 가진 operator를 의미합니다.

여기서 $V'$자리에 $V^\star$를 넣어주면, 다음이 성립합니다.

operator를 적용하면 적용할수록 optimal point에 가까워지니 당연히 수렴할 것입니다.

operator $\Pi$

operator $\Pi$는 다음을 정의합니다.

$\Omega$는 가능한 value function space를 이야기합니다. Neural network로 치면 parameter space라고 보시면 될 거 같습니다. 그 안에서 $V$와 가장 가까운 $V'$를 찾아 반환합니다. 이해가 잘 안갈 수 있을 것 같은데, $\mathcal{B}$와 함께 적용한 버전에서 이해해보시면 될 거 같습니다.

$\Pi$ 역시 다음과 같은 contraction의 성질을 만족하기 때문에 수렴을 보장하는 operator입니다.

convergence of algorithms

fitted value iteration 알고리즘은 다음과 같이 앞의 두 operator를 적용한 알고리즘입니다. Bellman operator를 적용한 값에 가장 가까운 $V'$를 찾는 알고리즘입니다.

그러나 두 operator 각각은 수렴성을 보장하지만, 이 알고리즘은 수렴을 보장할 수 없습니다. 그 이유는 다음과 같이 그림을 통해 이해해볼 수 있습니다.

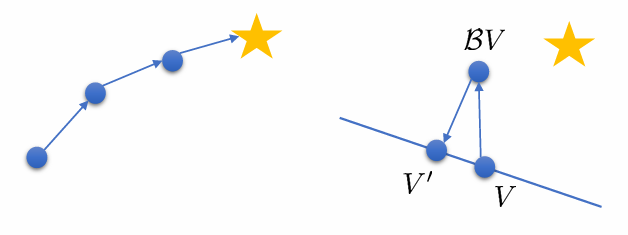
이 알고리즘은 $V$에 $\mathcal{B}$를 적용한 뒤 이에 가장 가까운(least square를 만드는) $V'$를 $\Omega$ 안에서 찾습니다. 즉 bellman operator로 아무리 optimal $V^\star$에 가까워져도 $V$는 $\Omega$ 안에서만 존재하기 때문에 다시 돌아올 수밖에 없는 것입니다.

이는 fitted Q-iteration에 대해서도 마찬가지입니다. 마찬가지로 두 operator를 정의하면 수렴하지 않음을 알 수 있습니다.

Q-learning은 어떨까요? Q-learning은 얼핏 보면 gradient descent를 사용하기 때문에 수렴하지 않나?라고 생각할 수 있지만 아닙니다. 우리는 bootstrapped된 target과의 error를 매번 줄일 뿐, 완전한 objective function의 값을 줄이는 게 아니기 때문입니다. 또 식을 풀어 써보면 target 값에 대한 올바른 chain rule을 적용하고 있지 않습니다. 따라서 Q-learning도 수렴을 보장하지 않습니다.

슬프게도 actor-critic 알고리즘에서도 $V$ fitting을 위해 bootstrapped target을 이용하기 때문에 $V$의 수렴을 보장할 수 없습니다.

그러나 실전에서 이런 알고리즘들은 잘 사용됩니다. 실전적인 방법으로 잘 작동하게 만들 수 있기 때문입니다. 이는 이후에 소개하도록 하겠습니다.

---

이로서 ch7에 대한 포스팅이 끝났습니다. 틀린 부분이나 이해가 안된 부분이 있다면 댓글 주세요!

CS285 website: https://rail.eecs.berkeley.edu/deeprlcourse/