[CS285] Ch8. Deep RL with Q-Functions

YJ·2025년 1월 30일

CS 285 DRL Deep Reinforcement Learning RL

CS 285

목록 보기

5/6

Deep Reinforcement Learning을 소개하는 Berkely CS 285 강좌의 Ch4~Ch9를 들으며 제 지식과 함께 정리해보고자 합니다. 강의 링크는 아래를 참고하세요.

https://rail.eecs.berkeley.edu/deeprlcourse/

제 나름의 지식을 많이 덧붙여 틀린 부분이 있을 수 있습니다. 발견하시면 댓글로 지적 부탁드립니다!
이해가 안되는 경우 질문도 환영입니다!

Ch8. Deep RL with Q-Functions

Correct Problems in Q-learning

Q-learning recap

ch7에서 배운 Q-learning 알고리즘은 위와 같았습니다. 한 time step의 data를 수집한 뒤 target 값을 바탕으로 sudo-gradient를 통해 Q-function을 update하는 방식이었습니다. 이 알고리즘은 두 가지 문제를 가지고 있습니다.

매 time-step의 data는 correlated 되어있다. 이는 bias를 유발한다.
$y_i$ 가 실제로는 $\phi$ 와 연관되어 있기 때문에, 올바른 gradient descent와 달리 moving target으로 인한 불안정성이 존재한다.

1번은 당연한 문제입니다. 로봇이 이동하는 상황이라면 $t+1$ 의 data는 $t$ 의 상황에서 크게 벗어나지 않을 것입니다. 하지만 우리의 학습 목표는 언제나 generalization이기 때문에, data 자체의 편향이 문제가 됩니다.

2번은 update 식이 sudo-gradient이기 때문에 발생합니다. 올바른 objective function의 gradient를 구한게 아니라는 것이죠. 하지만 max 함수가 들어있는 이상 실제 gradient를 구하는 것은 너무나 복잡합니다. 이 두 문제를 해결하는 방법에 대해 논의합니다.

Q-learning with replay buffers

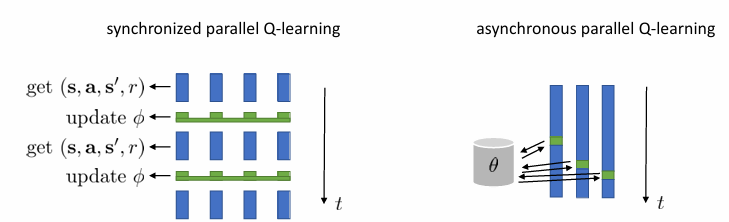
1번 문제를 해결하기 위해 떠올려볼 수 있는 방법은 batch를 이용하는 것입니다. batch를 이용하면 data의 편향성이 줄어들 것이기 때문입니다. 위와 같이 여러 개의 환경을 동시에 작동시켜 data를 얻을 수 있죠.

여기서는 새로운 방식을 제시합니다. 어차피 off-policy로 해도 되는데 online으로 작동시킬 필요가 있냐는 것입니다. 그냥 data를 엄청 많이 수집해놓고, 잘 섞어서 random sampling 하자는 것입니다.

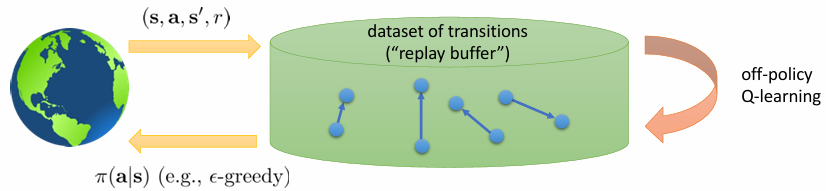
이렇게 random sampling할 수 있게 sample을 담아둔 것을 reaplay buffer $\mathcal{B}$ 라고 부릅니다. 그런데 어디 이상한 데서 policy를 데려오는 것도 무리기 때문에, $\epsilon -greedy$ 방법을 이용해서 중간중간 data를 보충하고, random으로 섞어서 다시 뽑고..의 방식을 이용합니다. 이렇게 정리된 알고리즘은 다음과 같습니다.

fitted Q-iteration과 다른 점은 update 식입니다. $\phi$ 를 argmin을 찾을 때까지 fitting 하는 fitted Q-iteration과는 다릅니다.

Q-learning with target networks

2번째 문제는 update하는 식이 sudo-gradient를 사용한다는 것이었습니다. Q-learning은 방금 말했듯 full fitted Q-iteration과는 다릅니다. $\phi$ 를 update 할 때 Q-learning은 $y_i$ 를 계산하고, sudo-gradient를 계산해서 한 번 fitting하는 과정을 거칩니다. Full fitted Q-iteration은 $\phi$ 를 update 할 때 argmin을 취합니다. 다시 말해, minimum이 계산 될 때까지 같은 $y_i$ 에 $Q$ 를 계속해서 fitting합니다. Moving target이 아니니 수렴이 더 안정적입니다.

이렇게 비교를 통해 full fitted Q-iteration처럼 target을 고정시켜 수렴 안정성을 되찾고 싶습니다. 다만 bootstrapped target을 이용하니 굳이 그 값으로 수렴할 필요는 없고, N번 정도 update할 동안 target을 고정시키고 싶습니다. 이렇게 target $y_i$ 를 구할 때 N번 동안 잠시 고정시켜놓은 $\phi$ value인 $\phi'$ 을 이용하는 것이 target network 방식입니다. 알고리즘을 정리하면 다음과 같습니다.

여기서 K=1인 것이 classic Q-learning 알고리즘인 DQN입니다.

그런데 조금 찝찝합니다. N번에 한 번 $\phi$ 를 고정시키면 그 다음 step에서는 $\phi$ 와 너무 비슷한 $\phi'$ 을 이용하게 될 거고, $N-1$ 번째 step에서는 $\phi$ 와 너무 다름 $\phi'$ 을 이용하게 될 것입니다. 이를 위해 5번에서 $\phi'$ 을 다음과 같이 update하는 식을 이용하기도 합니다.

\phi' \leftarrow \tau \phi' +(1-\tau)\phi

$\tau=0.999$ 가 잘 작동한다는 것이 알려져 있습니다. 즉, target을 거의 고정시켜놓고 우리의 $\phi$ 에 조금씩만 맞춰가는 것입니다.

A general view of Q-learning

이제 ch.7에서 배운 Q-learning의 문제를 다 해결했습니다. 지금까지 배운 알고리즘은 다음과 같이 3개의 process가 어떤 상대적 관계를 가지고 작동하느냐에 차이가 있습니다.

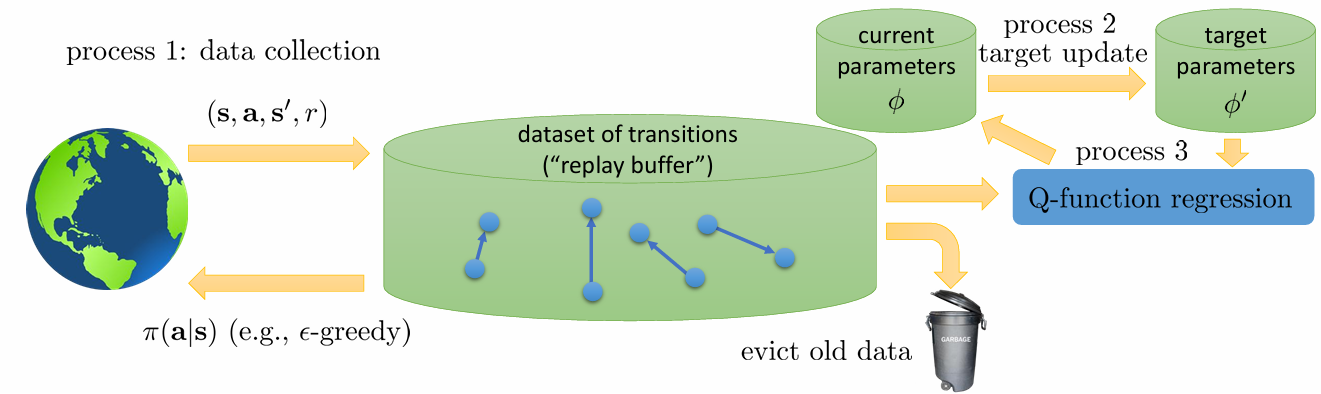
process 1은 data 수집입니다. process 2는 target을 update하는 주기입니다. process 3는 Q-function을 fitting하는 것입니다. 지금까지 배운 것들을 이 기준으로 살펴보겠습니다.

먼저 online Q-learning입니다. process 1 뒤에 process 2 그리고 process 3가 일어납니다. 세 process가 순차적으로 같은 속도로 일어납니다.

fitted Q-iteration입니다. process 1 안에 process 2 안에 process 3가 일어나죠. 즉 process 3 < process 2 < process 1 순으로 빠르게 일어납니다.

DQN은 process 1과 process 3는 매 step마다 일어나지만 process 2는 N번마다 일어납니다.

이렇듯 3개의 process를 어떤 상대적 시간으로 이용할 것인가만 다릅니다.

improving Q-learning

이 파트에서는 실제 구현에서 Q-learning이 잘 작동하도록 만드는 방법을 배웁니다. 다음은 Q-learning의 실제 작동 결과입니다.

Epoch가 갈 수록 실제 reward가 증가합니다.(불안정하지만), 우리의 Q-value는 스무스하게 증가합니다. 이는 당연합니다. 우리의 policy가 잘 학습된다면 기대 reward도 증가할 것입니다.

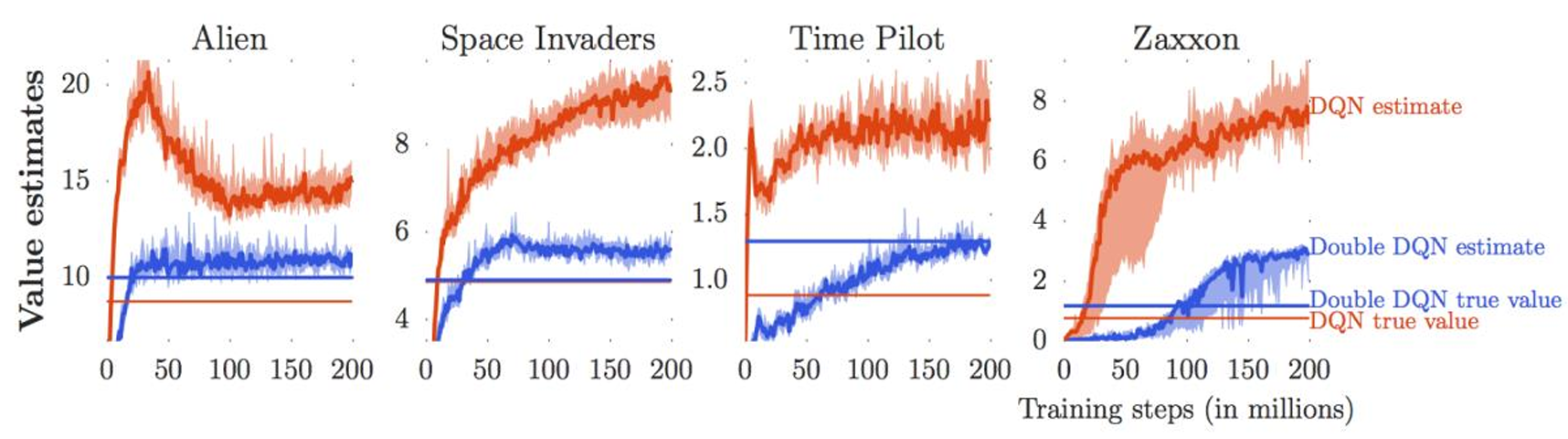
그런데 Q-value가 정확할까요? 위 그래프에서 실제 Q-value(빨간 직선)와 계산된 Q-value(빨간 그래프)를 비교해보면 Q-learning 알고리즘에서 계산되는 Q-function 값이 실제 값에 비해 overestimate 된 것을 확인할 수 있습니다. 왜일까요?

이는 다음과 같은 target 식이 항상 max를 취하기 때문에 발생합니다.

y_i = r(s_i, a_i) + \gamma \max_{a'} Q_{\phi'}(s', a') = r(s_i, a_i) + \gamma Q_{\phi'}(s', \argmax_{a'} Q_{\phi} (s',a') )

우리가 학습한 $\phi$ 는 처음에 noise를 포함하고 있습니다. 그런데 max를 매번 취함으로써 매번 기존 값보다 큰 noise를 취하게 된다는 것이죠.

Double Q-learning

이는 다음과 같이 target network 두 개를 사용함으로써 해결할 수 있습니다.

Q_{\phi_A} \leftarrow r(s_i, a_i) + \gamma Q_{\phi_B}(s', \argmax_{a'} Q_{\phi_A} (s',a') )

Q_{\phi_B} \leftarrow r(s_i, a_i) + \gamma Q_{\phi_A}(s', \argmax_{a'} Q_{\phi_B} (s',a') )

A를 update 할 때 action은 A에서 뽑으면서도 값은 B의 값을 취합니다. 즉, A에서 max noise가 포함된 action을 뽑아도 B에서는 max가 아닐 확률이 높으니, 이를 이용하는 것입니다.

두 개의 target network는 굳이 새로운 network를 정의할 필요 없이 $\phi$ 와 $\phi'$ 을 그대로 이용하는 경우가 많습니다.

Q-learning with N-step returns

y_i = r(s_i, a_i) + \gamma \max_{a'} Q_{\phi'}(s', a')

$\phi$ 에 noise가 포함되어 있으니, 위의 target에서 $\phi$ 가 주는 영향을 줄이고 싶습니다. 그러면 우리가 직접 얻은 sample return이 차지하는 비중을 늘려야 합니다. 다음과 같은 N-step return을 사용해보는 건 어떨까요?

y_{i,t} = \sum_{t'=t}^{t+N-1} \gamma^{t'-t} r(s_{i,t'}, a_{i,t'}) + \gamma^{t+N} \max_{a'_{i, t+N}} Q_\phi(s', a')

좋은 해결책으로 보입니다. 그러나 불행하게도 이 알고리즘은 반드시 on-policy로 작동해야 합니다. 현재 policy에 대한 $Q$ 의 estimation을 구하려면 trajectory가 현재 policy를 이용한 것이어야 하기 때문입니다. (N=1인 경우 $s,a, s'$ 가 현재 policy로부터 나왔고 $a'$ 가 max에 걸리는 값이라 상관 없습니다.)

이를 해결하는 방법은 다음과 같습니다.

그냥 무시하고 off-policy로: 그래도 잘 작동하는 경우가 꽤 있다고 합니다
N을 정해놓고 on-policy data를 이용합니다.
policy gradient에서도 쓰였던 importance sampling을 이용합니다.

Q-learning with continuous actions

지금까지 배운 Q-learning 알고리즘은 discrete action space를 가정했습니다. 그래야 $a$ 에 대한 max든 argmax든 쉽게 취할 수 있기 때문입니다. (단순 비교로) 그런데 action space가 continuous 해진다면 이 방법이 불가능해집니다. 이 때 어떻게 max를 구할 수 있을까요? 실제로 사용하는 방법들을 소개합니다.

Q-learning with stochastic optimization

첫번째 방법은 간단합니다. discrete 하다고 가정하고 그 discrete한 action을 임의 추출하여 max를 취하는 것이죠. 그렇게 정확하진 않지만 간단합니다. 더 정확도를 늘리고 싶으면 cross-entropy method가 CMA-ES와 같은 방법을 이용한다고 합니다.

Easily maximizable Q-functions

두번째 방법은 Q-function의 형태를 maximize하기 쉬운 형태로 고정하는 것입니다. 대표적으로는 다음과 같은 quadratic function이 있습니다.

Q(s,a) = - \frac{1}{2} (a-\mu_\phi(s))^T P_\phi(s)(a-\mu_\phi(s)) + V_phi(s)

그러면 argmax와 max는 다음과 같이 정리할 수 있을 것입니다.

\argmax_a Q_\phi(s,a) = \mu_\phi(s)

\max_a Q_\phi(s,a) = V_\phi(s)

그러나 Q-function의 형태를 제한하여 실제 Q-function을 반영하지 못하는 문제가 생길 수 있습니다.

Q-learning with maximizer approximater(DDPG)

세 번쨰 방법은 Q-function의 max를 학습하는 target network를 다시 학습하는 것입니다.

\mu_\theta(s) \approx \argmax_a Q_\phi(s,a)

그러면 $\mu$ 는 다음과 같이 update 할 수 있습니다.

\theta \leftarrow \argmax_\theta Q_\phi(s,\mu_\theta(s))

argmax는 결국 gradient ascent의 형태를 띌 것입니다. gradient는 다음과 같이 chain rule을 이용해 구합니다.

\frac{dQ_\phi}{d\theta} = \frac{da}{d\theta} \frac{dQ_\phi}{da}

이렇게 정리한 DDPG 알고리즘은 다음과 같습니다.

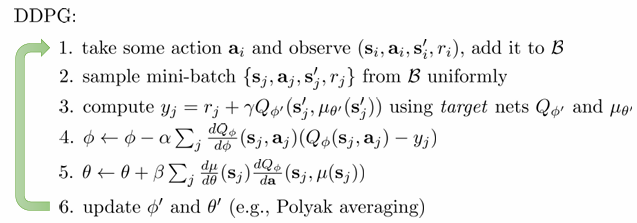
Implementation Tips and Examples

구현 팁은 아래와 같습니다.

먼저 쉽고 간단하고 안정적인 task에 먼저 적용하여 안정성과 구현 정확성을 테스트해야합니다.
large replay buffer, 즉 샘플 사이즈가 클수록 안정적입니다.
수렴하는 데 시간이 걸리니 기다릴 수 있어야 합니다.
epsilon-greedy 방식을 취하는 게 좋습니다.

조금 더 나아가면

Bellman error gradients가 클 수 있으니, gradient를 clip하거나 Huber loss를 이용해보아야 합니다.
double Q-learning이 도움이 됩니다.
N-step return이 도움이 되긴 하나, 문제가 되는 경우가 있습니다.
exploration 정도와 learning rate를 scheduling하고(시간이 지날수록 high to low로) Adam optimizer를 사용하는 것이 도움이 됩니다.

이로서 ch8에 대한 포스팅이 끝났습니다. 틀린 부분이나 이해가 안된 부분이 있다면 댓글 주세요!

CS285 website: https://rail.eecs.berkeley.edu/deeprlcourse/