[Python] 백준 / 가장 긴 바이토닉 부분 수열 / 11054번 / DP

DP 개념 바로가기

문제

가장 긴 바이토닉 부분 수열 문제 링크

수열 S가 어떤 수 Sk를 기준으로 S1 < S2 < ... Sk-1 < Sk > Sk+1 > ... SN-1 > SN을 만족한다면, 그 수열을 바이토닉 수열이라고 한다.

예를 들어, {10, 20, 30, 25, 20}과 {10, 20, 30, 40}, {50, 40, 25, 10} 은 바이토닉 수열이지만, {1, 2, 3, 2, 1, 2, 3, 2, 1}과 {10, 20, 30, 40, 20, 30} 은 바이토닉 수열이 아니다.

수열 A가 주어졌을 때, 그 수열의 부분 수열 중 바이토닉 수열이면서 가장 긴 수열의 길이를 구하는 프로그램을 작성하시오.

입력

첫째 줄에 수열 A의 크기 N이 주어지고, 둘째 줄에는 수열 A를 이루고 있는 Ai가 주어진다. (1 ≤ N ≤ 1,000, 1 ≤ Ai ≤ 1,000)

10
1 5 2 1 4 3 4 5 2 1

출력

첫째 줄에 수열 A의 부분 수열 중에서 가장 긴 바이토닉 수열의 길이를 출력한다.

7

• 접근 방식

  수열이 증가 하다가 감소할 수 있기 때문에 고점을 선택해야 하는데, 이 때 고점에서부터 왼쪽으로 감소하는 수열의 길이와 오른쪽으로 감소하는 수열의 길이 합이 최대여야 한다

따라서 왼쪽에서 증가하는 부분수열의 길이 dp를 구하고 오른쪽에서 증가하는 부분수열의 길이 dp를 구한 후 둘으 합이 큰 값을 출력 한다

1. 다음과 같이 초기화 한다

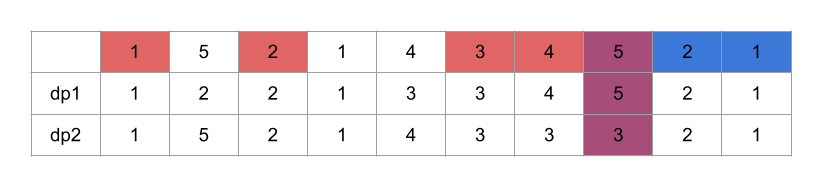
2. 현재 위치가 i일 때 처음부터 i-1 까지의 수가 i 보다 작은 dp1값과 dp1[i]값을 비교해 큰 값을 dp1[i]값에 넣는다

3. 반대방향으로 2번을 진행하여 dp2를 채운다
   

4. dp1과 dp2의 인덱스에 접근해 각각을 합한 값 중 큰 값에서 - 1(고점 중복) 한 값을 출력한다
   

코드

# url : https://www.acmicpc.net/problem/11054
# 난이도 : gold 3

n = int(input())

num_list = list(map(int,input().split()))

dp1 = [1] * n
dp2 = [1] * n

for i in range(n):
    for j in range(i):
        if num_list[i] > num_list[j] :
            dp1[i] = max(dp1[i], dp1[j]+1)


num_list = num_list[::-1]
for i in range(n):
    for j in range(i):
        if num_list[i] > num_list[j] :
            dp2[i] = max(dp2[i], dp2[j]+1)

dp2 = dp2[::-1]

print(max([dp1[i] + dp2[i] for i in range(n)])-1)