Mean Shift Clustering 개요
K-Means랑 유사한데 차이점은
- K-means는 중심에 소속된 데이터의 평균 거리 중심으로 이동하는 데 반해,
- Mean Shift는 중심을 데이터가 모여있는 밀도가 가장 높은 곳으로 이동 시킴
특징
- KDE (Kernel Density Estimation)로 확률 밀도 함수 (Probability Density Function)을 찾음
- KDE를 이용하여 데이터 포인트들이 데이터 분포가 높은 곳으로 이동하면서 군집화를 수행
- 별도의 군집화 개수를 지정하지 않고, 데이터 분포도에 기반하여 자동으로 군집 개수 선정
군집화 순서
1. 개별 데이터의 특정 반경 내에 주변 데이터를 포함한 데이터 분포도를 KDE 이용하여 계산
2. KDE로 계산된 데이터 분포도가 높은 방향으로 데이터 이동
3. 모든 데이터를 1-2까지 수행하면서 데이터를 이동, 개별 데이터들이 군집 중심점에 모임
4. 지정된 반복만큼 전체 데이터에 대해 KDE 기반으로 데이터를 이동시키면서 군집화 수행
5. 개별 데이터들이 모인 중심점을 군집 중심점으로 설정
그래서 KDE가 뭘까?
- 커널 함수를 통해 어떤 변수의 확률 밀도 함수를 추정하는 대표적인 방법
- 커널 함수는 대표적으로 가우시안 분포 함수 (정규 분포 함수)가 사용됨
: 커널 함수
: 확률 변숫값
: 관측값
: 대역폭(bandwidth)
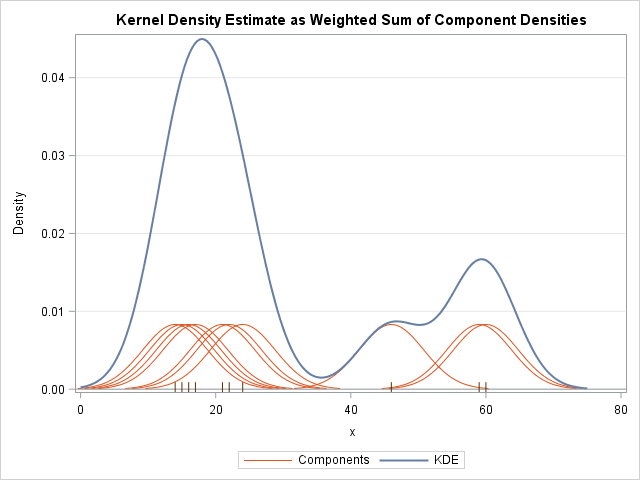
파란 그래프가 KDE고, 주황색이 개별 관측 데이터에 가우시안 커널 함수를 적용한 것임
각각의 커널 함수를 합쳐서 KDE를 만든다고 생각하면 될 듯
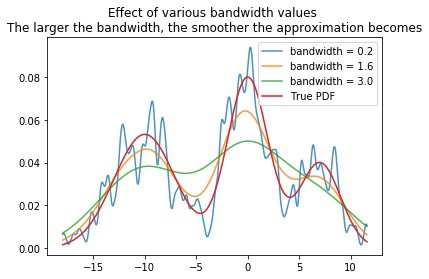
이렇게 대역폭(bandwidth)에 따라 그래프 모양에 변화가 생김
대역폭이 클수록 개별 커널 함수의 영향력이 적어져서 그래프가 부드러워짐
-> 과소적합 위험이 있음
대역폭이 작아지면 개별 커널 함수의 영향력이 커져서 그래프가 뾰족해지고
-> 과대적합 위험이 있음
KDE의 대역폭(bandwidth)을 계산하는 것은 매우 중요!
Mean Shift Clustering 실습
KDE 구하는 과정 먼저 보고 Mean Shift Clustering 실습하기
KDE 그래프 그리기
seaborn으로 KDE를 시각화해보자
원래distplot()을 이용하는 데 나중에 삭제된다는 경고메시지가 떠서
displot()으로 대체
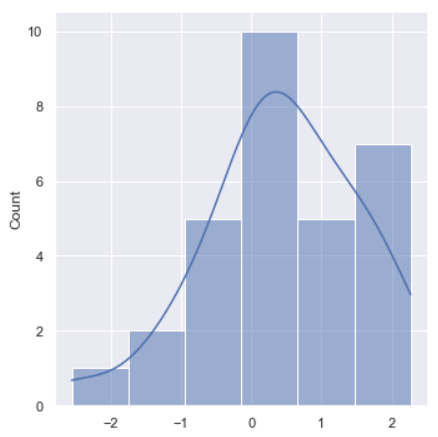
정규분포에서 샘플 30개를 뽑아서
히스토그램과 KDE를 겹쳐 그리기
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
sns.set(color_codes=True)
np.random.seed(0)
x = np.random.normal(0, 1, size=30)
sns.displot(x, kde=True)
rug=True하면 샘플이 어느쪽에 모여있는지 확인 가능
sns.displot(x, kde=True, rug=True)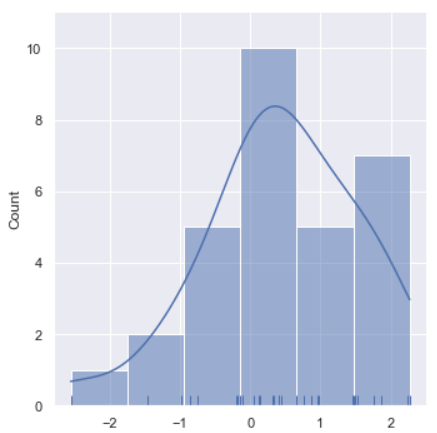
0 근처에 많이 있는 듯
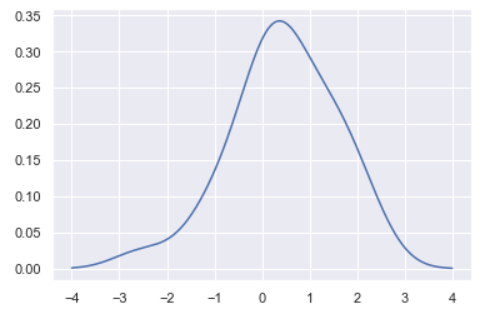
KDE가 어떻게 저렇게 나왔는지 단계별로 봐보자
우선 개별 관측 데이터에 대해 가우시안 커널 함수를 적용하자
bandwidth는 가우시안 커널일 때, 최적화 bandwidth에 근사하는 식임
from scipy import stats
np.random.seed(0)
x = np.random.normal(0, 1, size=30)
bandwidth = 1.06 * x.std() * x.size ** (-1 / 5.) # 가우시안일때, 최적화 bandwidth 근사
support = np.linspace(-4, 4, 200)
kernels = []
for x_i in x:
kernel = stats.norm(x_i, bandwidth).pdf(support)
kernels.append(kernel)
plt.plot(support, kernel, color="r")
sns.rugplot(x, color=".2", linewidth=3);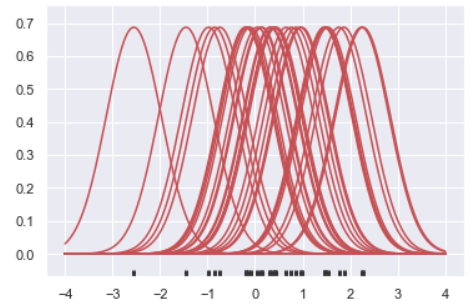
여기서 적절히 계산을 수행하면 KDE가 나옴
trapz는 적분 관련 함수인 거 같은데, 정확히는 모르겠음
from scipy.integrate import trapz
density = np.sum(kernels, axis=0)
density /= trapz(density, support)
plt.plot(support, density)Mean Shift Clustering 실습
scikit-learn으로 실습해보자
sklearn.cluster.MeanShift클래스를 제공함
make.blobs로 군집 샘플을 생성하고,
band_width=0.9로 Mean Shift Clustering 수행
import numpy as np
from sklearn.datasets import make_blobs
from sklearn.cluster import MeanShift
X, y = make_blobs(n_samples=200, n_features=2, centers=3,
cluster_std=0.8, random_state=0)
meanshift= MeanShift(bandwidth=0.9)
cluster_labels = meanshift.fit_predict(X)
print('cluster labels 유형:', np.unique(cluster_labels))cluster labels 유형: [0 1 2 3 4 5 6 7]기존 의도한 군집은 3개인데, 8개의 군집으로 너무 많이 세분화됨
따라서, 커널 함수의 bandwidth 크기를 1로 증가시키고 다시 군집화 진행
meanshift= MeanShift(bandwidth=1)
cluster_labels = meanshift.fit_predict(X)
print('cluster labels 유형:', np.unique(cluster_labels))cluster labels 유형: [0 1 2]군집이 3개로 됐음
scikit-learn은
estimate_banwidth()함수로 최적의 bandwidth를 계산해줌
quantile은 bandwidth를 구할 때 데이터를 어느정도 쓸 건지 정하는 것임
from sklearn.cluster import estimate_bandwidth
bandwidth = estimate_bandwidth(X,quantile=0.25)
print('bandwidth 값:', round(bandwidth,3))위에서 구한 최적의 bandwidth로 다시 군집화 진행
import pandas as pd
clusterDF = pd.DataFrame(data=X, columns=['ftr1', 'ftr2'])
clusterDF['target'] = y
# estimate_bandwidth()로 최적의 bandwidth 계산
best_bandwidth = estimate_bandwidth(X, quantile=0.25)
meanshift= MeanShift(best_bandwidth)
cluster_labels = meanshift.fit_predict(X)
print('cluster labels 유형:',np.unique(cluster_labels)) cluster labels 유형: [0 1 2]마찬가지로 3개의 군집이 만들어짐
K-Means Clustering 할 때 사용한 시각화 코드로 시각화해보자
import matplotlib.pyplot as plt
clusterDF['meanshift_label'] = cluster_labels
centers = meanshift.cluster_centers_
unique_labels = np.unique(cluster_labels)
markers=['o', 's', '^', 'x', '*']
for label in unique_labels:
label_cluster = clusterDF[clusterDF['meanshift_label']==label]
center_x_y = centers[label]
# 군집별로 다른 marker로 scatter plot 적용
plt.scatter(x=label_cluster['ftr1'], y=label_cluster['ftr2'], edgecolor='k',
marker=markers[label] )
# 군집별 중심 시각화
plt.scatter(x=center_x_y[0], y=center_x_y[1], s=200, color='white',
edgecolor='k', alpha=0.9, marker=markers[label])
plt.scatter(x=center_x_y[0], y=center_x_y[1], s=70, color='k', edgecolor='k',
marker='$%d$' % label)
plt.show()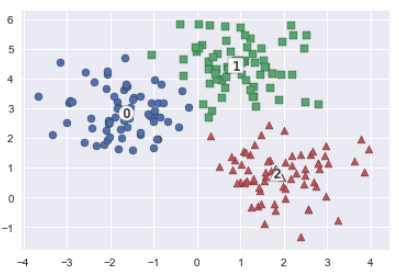
딱봐도 3개의 군집이 적당한 듯
print(clusterDF.groupby('target')['meanshift_label'].value_counts())target meanshift_label
0 1 67
1 2 67
2 0 65
2 1
Name: meanshift_label, dtype: int64샘플 1개만 빼면 나머지는 어느정도 의도한대로 군집화 되었음!