SVD 개요
SVD, Singular Value Decomposition, 특이값 분해
고윳값 분해와 비교
앞에서 배운 고윳값 분해와 비교해보자
고윳값 분해
- 정방행렬만 고유벡터로 분해
- PCA는 분해된 고유벡터에 원본 데이터를 투영하여 차원 축소
특이값 분해 (SVD)
- 정방행렬뿐만 아니라 행과 열의 크기가 다른 x 분해도 가능
- : 왼쪽 직교행렬
- : 오른쪽 직교행렬
- : 대각 행렬 (행렬의 대각 외의 나머지가 다 0)
- ,
- 의 대각에 위치한 값이 행렬 A의 특이값
SVD 유형
Full SVD
- 기본
Compact SVD
- 비대각 부분과 대각 원소가 0인 부분을 제거
Truncated SVD
- 대각 원소 가운데 상위 r 개만 추출하여 차원 축소
- 차원 축소 행렬 분해된 후 다시 분해된 행렬을 이용하여 원복된 데이터는 잡음이 제거된 형태로 재구성 됨
scikit-learn에서는 Truncated SVD로 차원 축소할 때 원본 데이터에 를 적용하여 차원 축소
SVD 활용
- 추천 엔진
- 문서의 잠재 의미 분석
- 이미지 압축/변환
- 의사(pseudo) 역행렬을 통한 모델 예측
SVD 실습
NumPy 에서 SVD를 지원한다.
이건 기본 SVD임
랜덤 행렬을 하나 만들자
# numpy의 svd 모듈 import
import numpy as np
from numpy.linalg import svd
# 4X4 Random 행렬 a 생성
np.random.seed(121)
a = np.random.randn(4,4)
print(np.round(a, 3))[[-0.212 -0.285 -0.574 -0.44 ]
[-0.33 1.184 1.615 0.367]
[-0.014 0.63 1.71 -1.327]
[ 0.402 -0.191 1.404 -1.969]]SVD 행렬 분해 진행
U, Sigma, Vt = svd(a)
print(U.shape, Sigma.shape, Vt.shape)
print('U matrix:\n',np.round(U, 3))
print('Sigma Value:\n',np.round(Sigma, 3))
print('V transpose matrix:\n',np.round(Vt, 3))(4, 4) (4,) (4, 4)
U matrix:
[[-0.079 -0.318 0.867 0.376]
[ 0.383 0.787 0.12 0.469]
[ 0.656 0.022 0.357 -0.664]
[ 0.645 -0.529 -0.328 0.444]]
Sigma Value:
[3.423 2.023 0.463 0.079]
V transpose matrix:
[[ 0.041 0.224 0.786 -0.574]
[-0.2 0.562 0.37 0.712]
[-0.778 0.395 -0.333 -0.357]
[-0.593 -0.692 0.366 0.189]]분해한 행렬을 다시 합쳐보자
# Sigma를 다시 0 을 포함한 대칭행렬로 변환
Sigma_mat = np.diag(Sigma)
a_ = np.dot(np.dot(U, Sigma_mat), Vt)
print(Sigma_mat)
print(np.round(a_, 3))[[3.4229581 0. 0. 0. ]
[0. 2.02287339 0. 0. ]
[0. 0. 0.46263157 0. ]
[0. 0. 0. 0.07935069]]
[[-0.212 -0.285 -0.574 -0.44 ]
[-0.33 1.184 1.615 0.367]
[-0.014 0.63 1.71 -1.327]
[ 0.402 -0.191 1.404 -1.969]]이번엔 Compact SVD를 실습해보자
데이터 의존도가 높은 원본 데이터 행렬을 생성하자
x 행렬인데, 가 2인 행렬이다.
a[2] = a[0] + a[1]
a[3] = a[0]
print(np.round(a,3))[[-0.212 -0.285 -0.574 -0.44 ]
[-0.33 1.184 1.615 0.367]
[-0.542 0.899 1.041 -0.073]
[-0.212 -0.285 -0.574 -0.44 ]]그냥 SVD 실행
U, Sigma, Vt = svd(a)
print(U.shape, Sigma.shape, Vt.shape)
print('Sigma Value:\n',np.round(Sigma,3))(4, 4) (4,) (4, 4)
Sigma Value:
[2.663 0.807 0. 0. ]0인 부분을 제거하고 앞에 두 행만 남겨두는 것으로 Compact SVD가 된다.
원본 행렬 복원까지 진행하자
# U 행렬의 경우는 Sigma와 내적을 수행하므로 Sigma의 앞 2행에 대응되는 앞 2열만 추출
U_ = U[:, :2]
Sigma_ = np.diag(Sigma[:2])
# V 전치 행렬의 경우는 앞 2행만 추출
Vt_ = Vt[:2]
print(U_.shape, Sigma_.shape, Vt_.shape)
# U, Sigma, Vt의 내적을 수행하며, 다시 원본 행렬 복원
a_ = np.dot(np.dot(U_,Sigma_), Vt_)
print(np.round(a_, 3))(4, 2) (2, 2) (2, 4)
[[-0.212 -0.285 -0.574 -0.44 ]
[-0.33 1.184 1.615 0.367]
[-0.542 0.899 1.041 -0.073]
[-0.212 -0.285 -0.574 -0.44 ]]마지막으로 Truncated SVD를 이용해 행렬분해를 해보자
scipy가 Truncated SVD를 지원한다.
단, 희소행렬만 가능하다.
import numpy as np
from scipy.sparse.linalg import svds
from scipy.linalg import svd
# 원본 행렬을 출력하고, SVD를 적용할 경우 U, Sigma, Vt 의 차원 확인
np.random.seed(121)
matrix = np.random.random((6, 6))
print('원본 행렬:\n',matrix)
U, Sigma, Vt = svd(matrix, full_matrices=False)
print('\n분해 행렬 차원:',U.shape, Sigma.shape, Vt.shape)
print('\nSigma값 행렬:', Sigma)
# Truncated SVD로 Sigma 행렬의 특이값을 4개로 하여 Truncated SVD 수행.
num_components = 4
U_tr, Sigma_tr, Vt_tr = svds(matrix, k=num_components)
print('\nTruncated SVD 분해 행렬 차원:',U_tr.shape, Sigma_tr.shape, Vt_tr.shape)
print('\nTruncated SVD Sigma값 행렬:', Sigma_tr)
matrix_tr = np.dot(np.dot(U_tr,np.diag(Sigma_tr)), Vt_tr) # output of TruncatedSVD
print('\nTruncated SVD로 분해 후 복원 행렬:\n', matrix_tr)원본 행렬:
[[0.11133083 0.21076757 0.23296249 0.15194456 0.83017814 0.40791941]
[0.5557906 0.74552394 0.24849976 0.9686594 0.95268418 0.48984885]
[0.01829731 0.85760612 0.40493829 0.62247394 0.29537149 0.92958852]
[0.4056155 0.56730065 0.24575605 0.22573721 0.03827786 0.58098021]
[0.82925331 0.77326256 0.94693849 0.73632338 0.67328275 0.74517176]
[0.51161442 0.46920965 0.6439515 0.82081228 0.14548493 0.01806415]]
분해 행렬 차원: (6, 6) (6,) (6, 6)
Sigma값 행렬: [3.2535007 0.88116505 0.83865238 0.55463089 0.35834824 0.0349925 ]
Truncated SVD 분해 행렬 차원: (6, 4) (4,) (4, 6)
Truncated SVD Sigma값 행렬: [0.55463089 0.83865238 0.88116505 3.2535007 ]
Truncated SVD로 분해 후 복원 행렬:
[[0.19222941 0.21792946 0.15951023 0.14084013 0.81641405 0.42533093]
[0.44874275 0.72204422 0.34594106 0.99148577 0.96866325 0.4754868 ]
[0.12656662 0.88860729 0.30625735 0.59517439 0.28036734 0.93961948]
[0.23989012 0.51026588 0.39697353 0.27308905 0.05971563 0.57156395]
[0.83806144 0.78847467 0.93868685 0.72673231 0.6740867 0.73812389]
[0.59726589 0.47953891 0.56613544 0.80746028 0.13135039 0.03479656]]scikit-learn도
TruncatedSVD클래스를 지원한다.
사실 scikit-learn에서 PCA를 할 때 SVD 행렬 분해를 이용함
그래서 둘이 매우 유사함
iris의 4개의 Feature를 2개로 차원 축소 진행
from sklearn.decomposition import TruncatedSVD, PCA
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
%matplotlib inline
iris = load_iris()
iris_ftrs = iris.data
# 2개의 주요 component로 TruncatedSVD 변환
tsvd = TruncatedSVD(n_components=2)
tsvd.fit(iris_ftrs)
iris_tsvd = tsvd.transform(iris_ftrs)
# Scatter plot 2차원으로 TruncatedSVD 변환 된 데이터 표현. 품종은 색깔로 구분
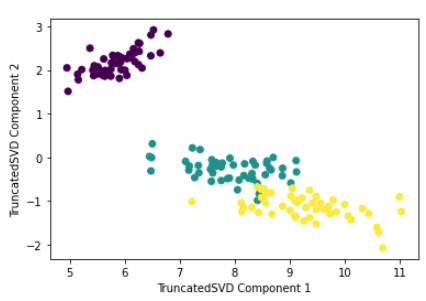
plt.scatter(x=iris_tsvd[:,0], y= iris_tsvd[:,1], c= iris.target)
plt.xlabel('TruncatedSVD Component 1')
plt.ylabel('TruncatedSVD Component 2')잘 분리 됨, setosa는 특히 잘 분리 됐음
StandardScaler까지 적용하고 SVD와, PCA와 비교해보기
from sklearn.preprocessing import StandardScaler
# iris 데이터를 StandardScaler로 변환
scaler = StandardScaler()
iris_scaled = scaler.fit_transform(iris_ftrs)
# 스케일링된 데이터를 기반으로 TruncatedSVD 변환 수행
tsvd = TruncatedSVD(n_components=2)
tsvd.fit(iris_scaled)
iris_tsvd = tsvd.transform(iris_scaled)
# 스케일링된 데이터를 기반으로 PCA 변환 수행
pca = PCA(n_components=2)
pca.fit(iris_scaled)
iris_pca = pca.transform(iris_scaled)
# TruncatedSVD 변환 데이터를 왼쪽에 PCA변환 데이터를 오른쪽에 표현
fig, (ax1, ax2) = plt.subplots(figsize=(9,4), ncols=2)
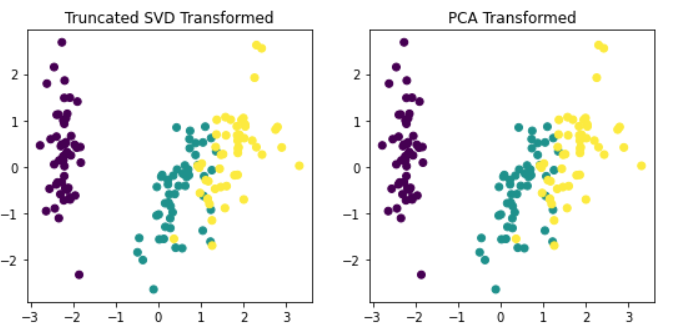
ax1.scatter(x=iris_tsvd[:,0], y= iris_tsvd[:,1], c= iris.target)
ax2.scatter(x=iris_pca[:,0], y= iris_pca[:,1], c= iris.target)
ax1.set_title('Truncated SVD Transformed')
ax2.set_title('PCA Transformed')거의 동일함 (같다고 봐도 됨)
NMF (참고)
NMF, Non Negative Matrix Factorization, 음수 미포함 행렬 분해
원본 행렬 내의 모든 원소 값이 모두 양수라는 게 보장되면 좀 더 간단하게 두 개의 기반 양수 행렬로 분해될 수 있는 기법
ex)
행렬 분해: SVD 같은 행렬 분해 기법 통칭
-> 분해된 행렬은 Latent Factor(잠재 요소)를 특성으로 가짐
-> : 원본 행에 대해 이 잠재 요소 값이 얼마나 되는지 대응 (행 크기가 와 같음)
-> : 이 잠재 요소가 원본 열로 어떻게 구성됐는지를 나타냄 (열 크기가 와 같음)
실습
from sklearn.decomposition import NMF
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
%matplotlib inline
iris = load_iris()
iris_ftrs = iris.data
nmf = NMF(n_components=2)
nmf.fit(iris_ftrs)
iris_nmf = nmf.transform(iris_ftrs)
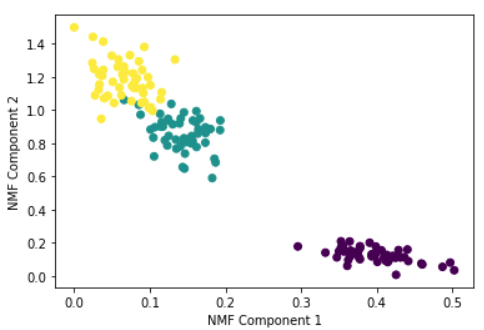
plt.scatter(x=iris_nmf[:,0], y= iris_nmf[:,1], c= iris.target)
plt.xlabel('NMF Component 1')
plt.ylabel('NMF Component 2')