[ML] 회귀 - 로지스틱 회귀 (Logistic Regression)

잘못된 내용 있으면 정정해주세요..

로지스틱 회귀 개요

로지스틱 회귀 개요

로지스틱 회귀는 이름은 회귀인데, 분류에 사용됨

종속변수가 범주형 변수일 때 사용하는 것이 로지스틱 회귀

---

시그모이드 함수

우선 시그모이드 함수를 먼저 알아보자 (로지스틱 함수라고도 함)

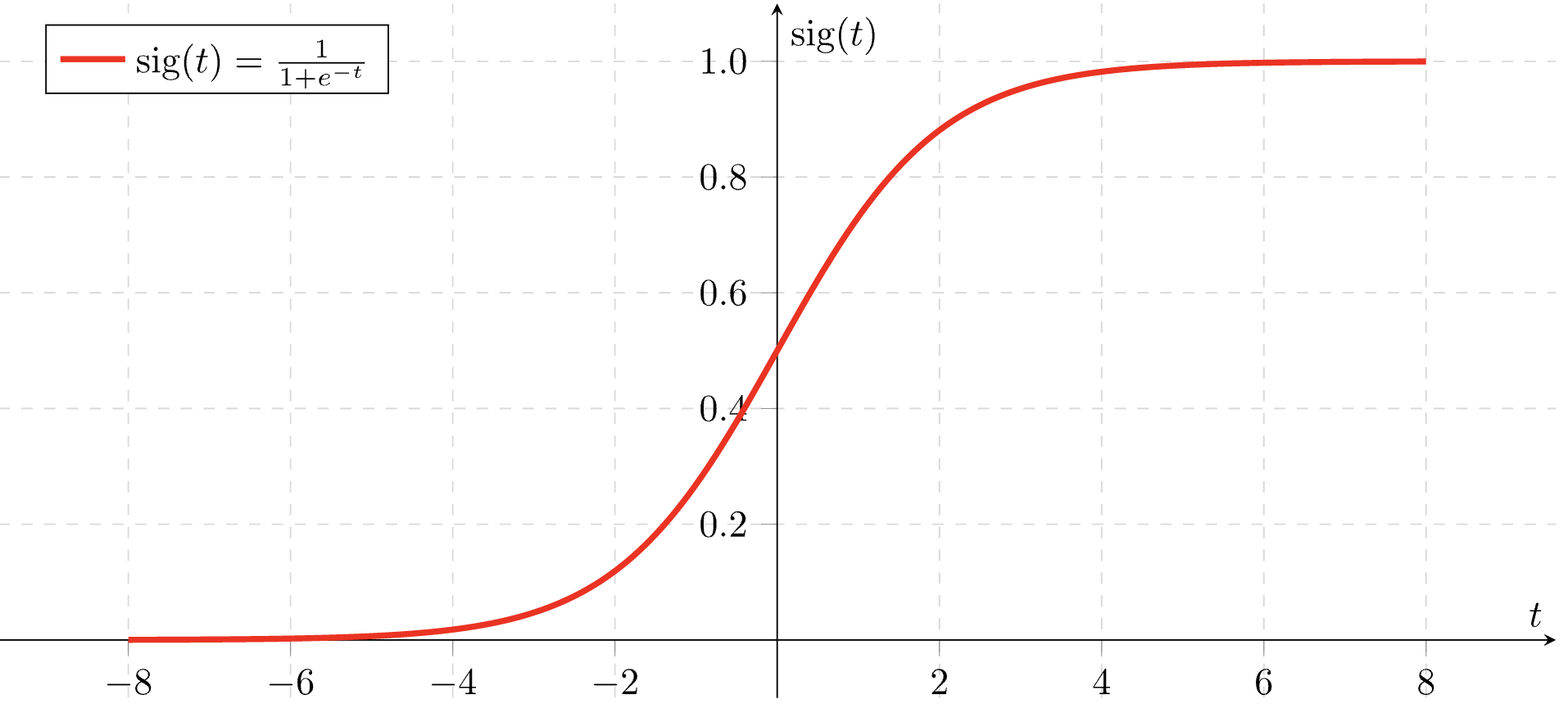
선형이 아닌 S-커브의 함수
보이는 것처럼 $0\leq Sigmoid(x)\leq1$ 범위를 가짐

---

오즈 (odds)와 로짓 (logit)

오즈는 승산이라고도 함

오즈: 발생하지 않을 확률 대비 일어난 확률의 비율

발생할 확률을 $P$라고 했을 때, 오즈는 다음과 같음

$P \rightarrow 0$일 때, $odds = 0$
$P \rightarrow 1$일 때, $odds = \infty$

즉, $0\leq odds\leq\infty$ 범위를 가짐


로짓(logit)은 odds에 log 변환한 것임

따라서, $-\infty\leq \log(odds) = logit\leq\infty$ 범위를 가짐

그래서 이게 왜 필요한데?

다중 선형 회귀 식을 보자

여기서 $y$가 범주형이면 좌변과 우변의 범위가 맞지 않음
(우변의 범위는 무한한데 좌변의 범위는 이진 분류이면 $y=0$ 또는 $y=1$)
그래서 $y$를 $logit$으로 바꿔주고 최종적으로 확률에 대한 식으로 나타내는 것이 목표!

그럼 다음과 같이 나온다.

이걸 $P$에 대한 식으로 변형하면 다음과 같다.

우리가 위에서 봤던 시그모이드 함수 꼴이다!

따라서, 독립변수와 회귀계수에 따라서 종속변수 $P$가 0과 1사이 값으로 나오게 되고,
분류를 할 때는 일반적으로 0.5를 기준으로 설정하면 되는 것!

---

로지스틱 회귀 기타 특징

1. 로지스틱 회귀는 주료 이진 분류로 사용 (다중도 가능)
2. 가볍고 빠르며 희소한 데이터 세트 분류에 성능이 좋음 (텍스트 분류)
3. 단, 요즘 XGBoost, LightGBM의 성능이 좋아서 주로 사용되진 않는 듯?

---

로지스틱 회귀 실습

scikit-learn에서는 LogisticRegression 클래스로 지원


주요 하이퍼 파라미터

• penalty: 규제 유형 설정 (l1, l2)
  -> l1: L1 규제 적용
  -> l2: L2 규제 적용
• solver: 회귀 계수 최적화 방식 지정
  -> 이전에는 libnear가 기본, 지금은 lbfgs가 기본
  -> lbfgs: 메모리 공간 절약, CPU 코어 수 많으면 최적화를 병렬로 수행
  -> liblinear: 다차원이고 작은 데이터 세트에서 효과적으로 동작
  -> 국소 최적화 (Local Minimum) 이슈 있음
  -> 병렬로 최적화 불가
  -> 그외 newtron-cg, sag, saga 있는데 성능에 큰 차이 없어서 변경할 일 없음
• C: 규제 강도 조절
  -> $\alpha$의 역수
  -> 그러니까 작을수록 규제 강도가 큼

cf) lbfgs는 L2 규제만 됨

유방암 데이터 사용

import pandas as pd
from sklearn.datasets import load_breast_cancer
from sklearn.linear_model import LogisticRegression

cancer = load_breast_cancer()

LogisticRegression은 스케일링이 선수되어야 함

from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split

scaler = StandardScaler()
feature_scaled = scaler.fit_transform(cancer.data)

X_train, X_test, y_train, y_test = train_test_split(feature_scaled, cancer.target, test_size = 0.2, random_state = 12)

scikit-learn 1.0.2 기준으로 solver='lbfgs' 가 기본값

from sklearn.metrics import roc_auc_score

lrc = LogisticRegression() # sklearn 1.0.2 기준 solver='lbfgs' 기본값
lrc.fit(X_train, y_train)

pred = lrc.predict(X_test)

score = roc_auc_score(y_test, pred)

print('ROC AUC Score: ', round(score,4))

ROC AUC Score:  0.9792

solver간 Score 비교

solvers = ['lbfgs', 'liblinear', 'newton-cg', 'sag', 'saga']

for solver in solvers:
    lrc = LogisticRegression(solver = solver, max_iter = 500)
    lrc.fit(X_train, y_train)
    
    pred = lrc.predict(X_test)

    score = roc_auc_score(y_test, pred)

    print(solver, 'ROC AUC Score: ', round(score,10))

lbfgs ROC AUC Score:  0.9791666667
liblinear ROC AUC Score:  0.9791666667
newton-cg ROC AUC Score:  0.9791666667
sag ROC AUC Score:  0.9791666667
saga ROC AUC Score:  0.9791666667

현재 환경에서는 solver간 ROC AUC Score 차이 없음
-> 실제로 solver가 크게 중요하지 않음

GridSearchCV 진행

from sklearn.model_selection import GridSearchCV

params = {'solver': ['liblinear', 'lbfgs'], 'penalty': ['l1', 'l2'], 'C': [0.01, 0.1, 1, 5, 10]}

lrc = LogisticRegression()

lrc_grid = GridSearchCV(lrc, param_grid = params, scoring='roc_auc', cv = 5)

lrc_grid.fit(feature_scaled, cancer.target)

print('최적 하이퍼 파라미터:', lrc_grid.best_params_, '\nROC AUC Score:', round(lrc_grid.best_score_, 4))

최적 하이퍼 파라미터: {'C': 0.1, 'penalty': 'l2', 'solver': 'liblinear'} 
ROC AUC Score: 0.9954

lbfgs는 l1 규제 적용이 안 돼서 오류 발생함
그외의 것들 중 최적 하이퍼 파라미터 조합을 찾은 듯