조건부 확률
- p(E|F) = P(EF) / P(F) for p(F) > 0
AB는 교환법칙이 성립하기 때문에 아래식은 같습니다. P(AB) = P(A)P(B|A) = P(B)P(A|B).
P(A|B) = P(AB) / p(B)입니다. P(B|A) = P(AB) / P(B) 입니다. 그러므로 P(AB) = P(A)P(B|A) = P(B)P(A|B) 입니다.
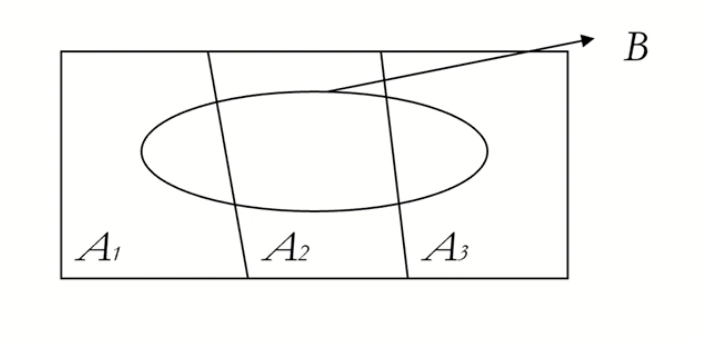
A1,A2,A3가 샘플 s의 부분이고, A1,A2,A3가 상호 베타적이라고 가정하면 B는 밑에 사진처럼 표현을 할수 있습니다. 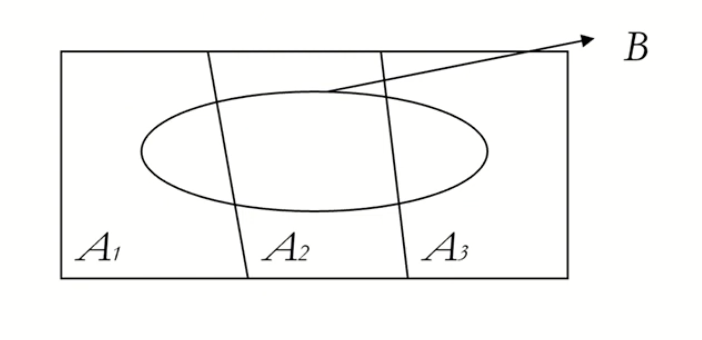
이런 가정일때, 밑에식은 성립합니다.
Law of Total Probability
P(B) = P(A1 n B) + P(A2 n B) + P(A3 n B)
= p(A1)P(B|A1) + P(A2)P(B|A2) + P(A3)P(B|A3)
이제 저희가 P(A1), P(A2),P(A3), P(B|A1), P(B|A2),P(B|A3)를 알고 있다고 가정을 합시다.
저희가 알고 싶은 확률은 P(A1|B), P(A2|B), P(A3|B)입니다. 이 확률은 밑에 식에 의해서 알수 있습니다.
P(A1|B) = P(A1B)/P(B) = P(A)P(B|A1) / P(B)
= P(A)P(B|A1) / P(A1)P(B|A1) + P(A2)P(B|A2) + P(A3)P(B|A3)입니다.
나머지도 이런식으로 구할수가 있습니다.
Bayes'Rule은 P(A1), P(A2),P(A3), P(B|A1), P(B|A2),P(B|A3), 즉 Prior Probabability또는 Data Probablity를 알고 있을때 사후확률(P(A1|B), P(A2|B), P(A3|B))을 알수 있다는 것입니다.
다시말해서, 사후확률은 사전확률의 업데이트 된 버젼이라고 할수 있습니다. 예를들어, P(A1|B)는 P(A1)에서 B의 정보가 업데이트 되어 확률을 다시 재정의 하는것입니다.