Statistic

Population의 정의는 아래와 같다.Population: Collection of all items of interest 이 population을 N이라고 부른다.population을 사용하면서 나오는 숫자를 parameters이라 정의한다.반면에, Sample의

데이터는 크게 두 가지 유형으로 나뉩니다:1\. Categorical과 2. Numerical.Categorical DataCategorical data는 카테고리나 그룹을 설명합니다. 예를 들어, 차 브랜드에서는 BMW, Audi, Mercedes와 같은 것들이 있습

Qualitative (질적 측정)a. Nominal (명목 척도)명목 척도는 카테고리로 나눌 수 있지만 숫자나 순서는 관련이 없습니다. 예를 들어, 자동차 브랜드를 벤츠, 아우디, 현대 등으로 분류할 수 있습니다. 이때 순서나 수치적 가치는 중요하지 않습니다.b. O

평균(mean)은 데이터의 합을 개수로 나눈 값입니다. Outlier가 있을 경우, 평균은 왜곡될 수 있습니다.중앙값(median)은 데이터를 순서대로 나열했을 때 중간에 위치하는 값입니다. 데이터의 개수가 홀수일 경우 중간 값을, 짝수일 경우 중간 두 값의 평균을 사

확률 변수를 알기 위해서는 우선 표본 공간을 이해해야 한다.실험으로부터 나온 모든 결과를 담고 있는 집합.표본공간에서 담고 있는 원소들을 실수로 바꾼다.이때 원소들을 실수로 바꾸는 역할을 하는것이 확률 변수이다. 확률 변수는 함수로 작용을 한다.표본공간의 원소들을 실수

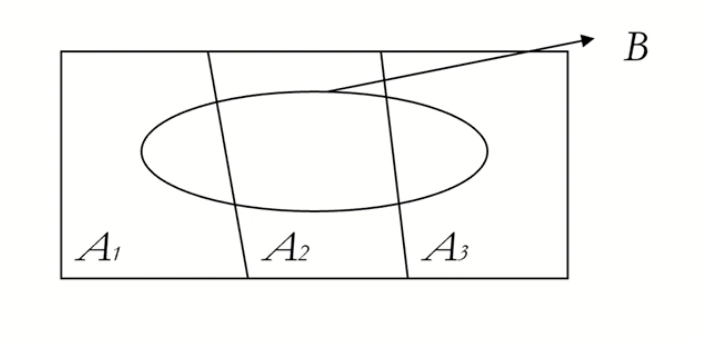
조건부 확률p(E|F) = P(EF) / P(F) for p(F) > 0AB는 교환법칙이 성립하기 때문에 아래식은 같습니다. P(AB) = P(A)P(B|A) = P(B)P(A|B).P(A|B) = P(AB) / p(B)입니다. P(B|A) = P(AB) / P(B)

두 사건 A와 B가 독립적이라고 가정할 때, 다음 조건이 충족되어야 합니다:P(B|A) = P(B)사건 A의 발생이 사건 B의 확률에 영향을 미치지 않음을 의미합니다.이 조건을 다른 식에 적용하면 다음과 같은 결과를 얻을 수 있습니다:P(AB) = P(A)P(B|A)

Discrete random variable의 기대값(EX)은 아래 식으로 나타낼 수 있습니다.$$EX = \\sum\_{i}x_if_x(x_i)$$EX는 random variable X의 expected value입니다. EX는 X의 가능한 value에서의 weigh

표본공간에서 확률 분포가 나오는 과정은 다음과 같습니다:1\. 표본공간 -> Random variable에 따라 실수 값으로 변환2\. 이 실수 값을 probability function을 통해 확률 값으로 변환3\. 이 확률들의 패턴이 확률 분포가 됨확률 함수로부터

포아송 분포는 단위 시간 안에 특정 사건이 몇 번 발생할 것인지를 표현하는 확률 분포입니다.포아송 분포는 이항 분포에서 계산상의 문제를 해결하기 위해 만들어졌습니다.예를 들어, 시행 횟수(n)가 360이고 p가 0.001일 때 이항 분포의 계산을 하려면 360!을 계산

첫 번째 성공이 일어날 때까지 Bernoulli trial을 실행할 횟수$$P(X = n) = (1-p)^{n-1}p, \\quad n=1,2,\\ldots$$예를 들어, n=5인 경우는 5번의 시행 후 첫 번째 성공을 의미합니다.$$\\sum{n=1}^{\\infty