선형대수 수기(1)- 행렬의 시작: homogenuous coordinates, matrix, vector

독학으로 선형 대수학을 공부했기 때문에 문제가 있을 수 있습니다. 제가 스스로 이해하기 위해 작성하는 것이라 실수가 있다면, 댓글 달아주세요!!

그래픽을 다루는데 있어서 Coordinate(좌표)는 상당한 의미를 가지고 있다. 어떤 object를 display에 표현하기 위해서는 카메라의 유형에 따라 적당한 위치에 표현하는 것이 중요하기 때문이다. 일반적으로 3d 그래픽에서는, 벡터(vector)를 사용해 좌표를 표시한다. 벡터는 크기(magnitude)와 방향(direction)을 모두 가진 개체(entity)로, 공간에서 그 지점의 위치를 표시하는 위치 벡터와 방향, 지향점을 표시하는 방향 벡터를 표시하는데 사용한다.

왜 3차원 좌표를 계산하는데 4차원의 행렬, 벡터를 사용하는가?

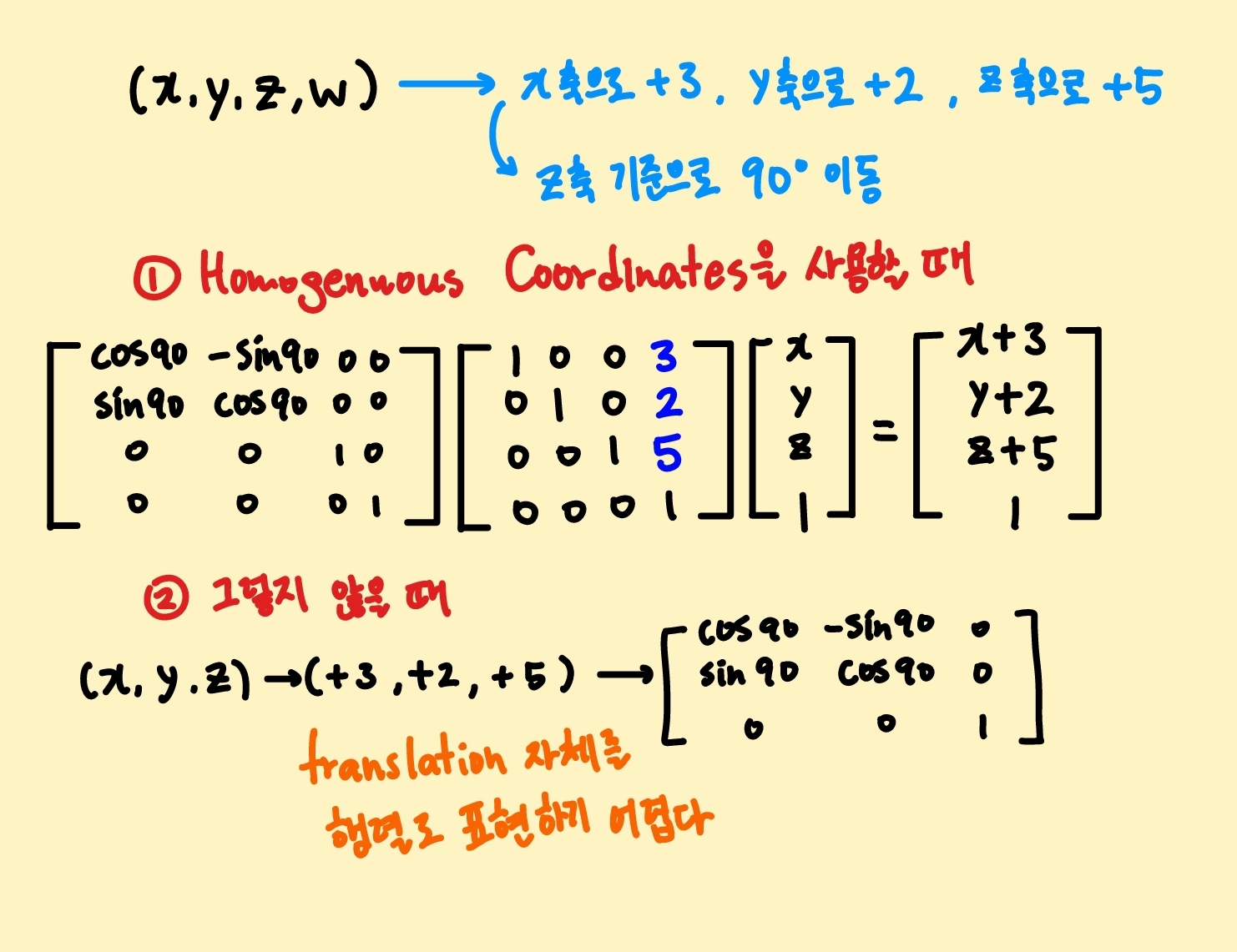
• 일반적으로 3차원의 좌표를 계산하기 위해서는, (x,y,z)에 w를 더한 4차원의 행렬과 벡터를 사용한다. 이러한 좌표를 Homogenuous Coordinates라고 부르며, 마지막에 추가한 w축은 일반적으로 1의 값을 유지한다. 이는 벡터, 행렬 연산이 보다 직관적으로 이해할 수 있게 만들어 준다. 이에 더해, translation(이동), scaling(크기 변환), rotation(회전) 등 여러 변환이 한번에 일어나는 벡터, 행렬 연산에서 하나의 행렬으로 여러 연산을 한꺼번에 담아낼 수 있다는 장점이 있다

ex. 좌표를 x축으로 3, y축으로 2, z축을 5를 이동시켜주는 연산(행렬을 곱하는 연산)을 할 때

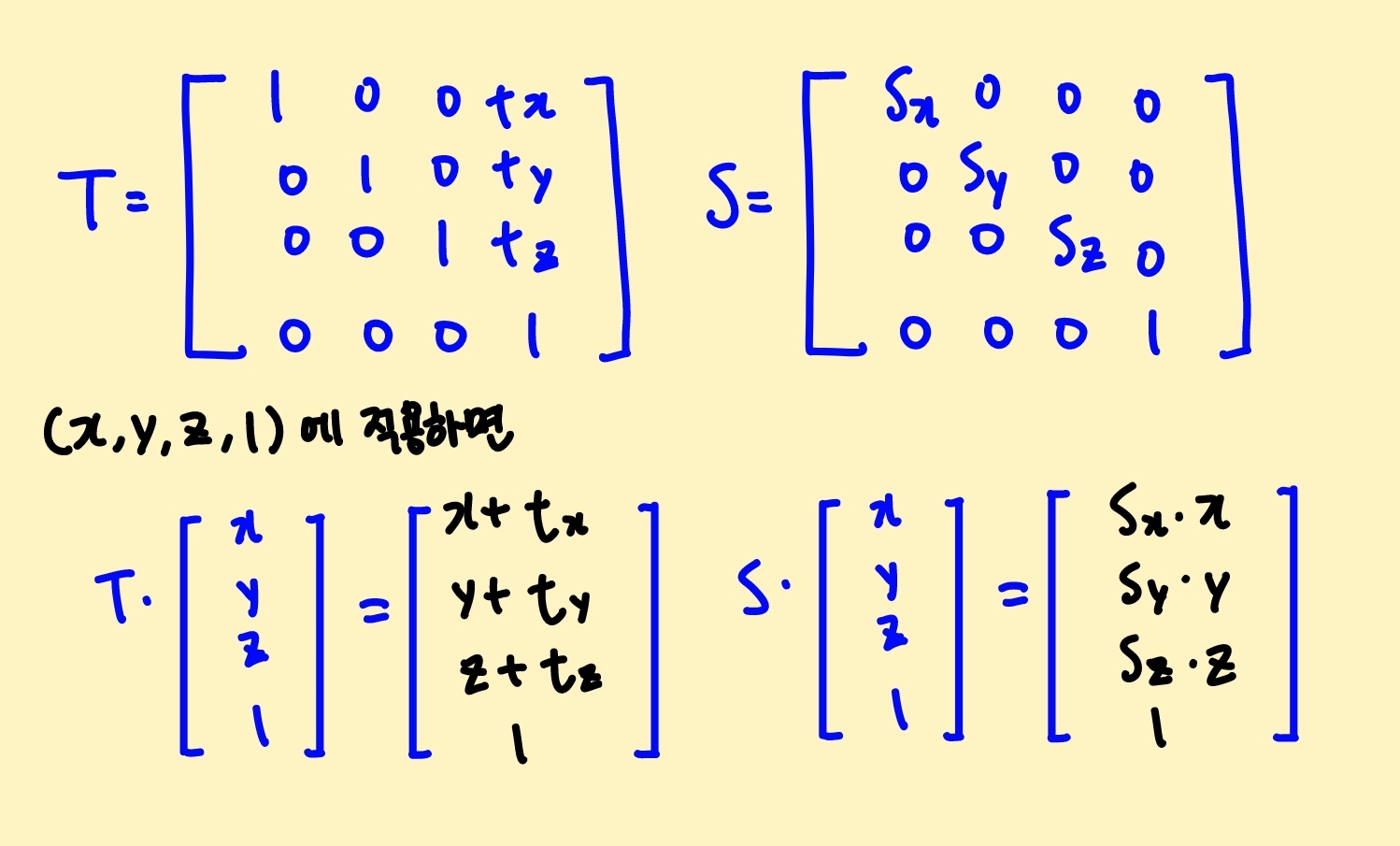
행렬 연산과 그것을 이해하기 위해: translation과 scaling

• 벡터에 행렬을 곱하는 것이 위치 벡터 또는 방향 벡터의 변환을 의미한다면, 행렬과 행렬의 곱은 각 행렬이 담은 변환을 하나의 행렬로 만드는 작업이다.
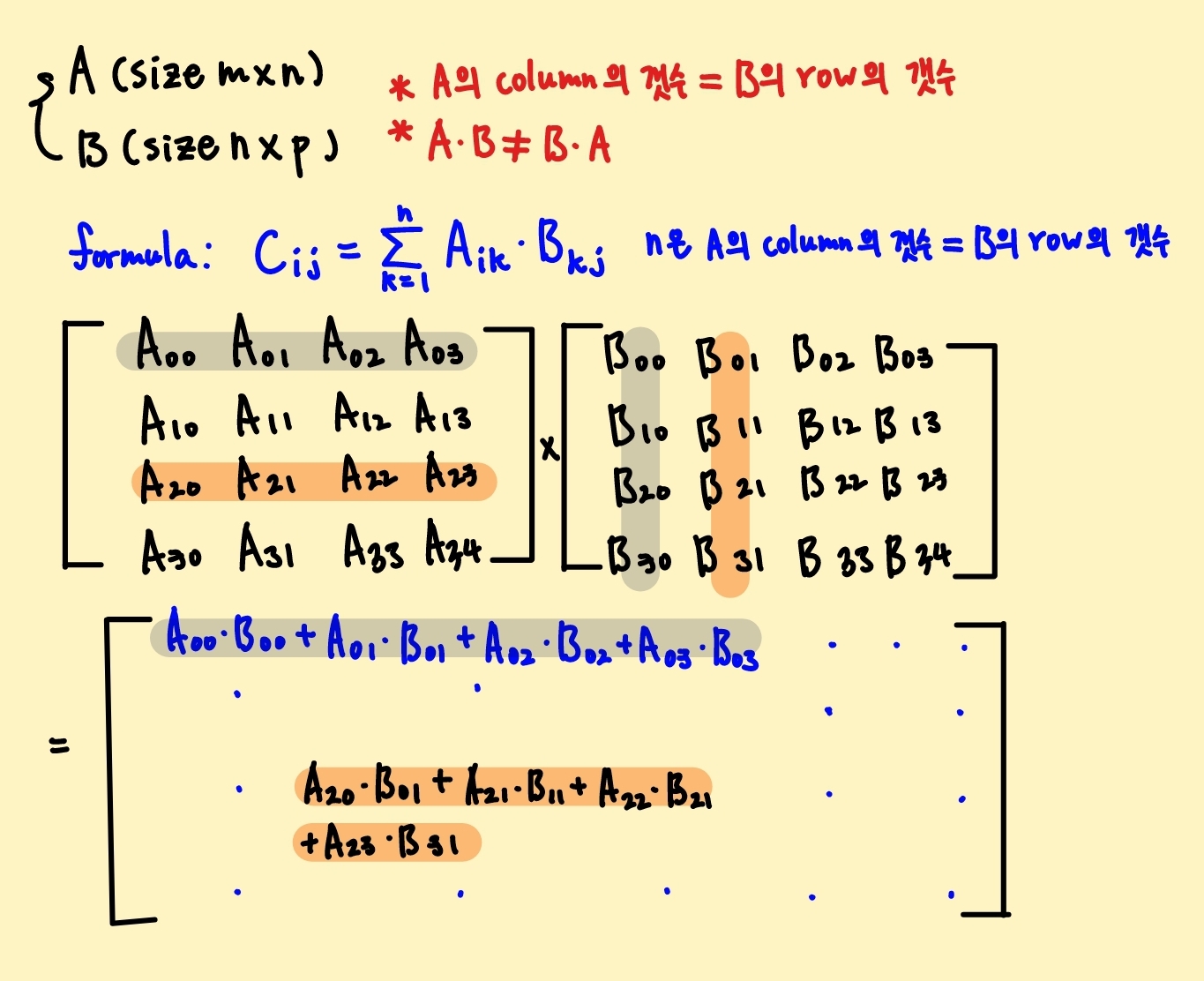
• 행렬과 행렬의 곱은 아래의 그림과 같이 벡터 A와 벡터 B의 대응되는 값의 외적값으로 채워진다. A 행렬의 column의 갯수와 B행렬의 row의 갯수는 동일해야 하는데, 이는 행렬과 벡터의 곱에서 동일하게 오른쪽의 entity가 우선되는 특성에 따라, 오른쪽의 entity의 dimension을 유지되도록 하기 위해서이고, 이후 연쇄적인 행렬, 벡터 연산을 용이하게 해줄 수 있다!

• 3d 그래픽에서 사용되는 행렬 중 translation(이동)과 scaling(크기 변환) 행렬은 3d 그래픽에서 가장 기본적인 변환을 이해하는데 도움이 된다